二叉树

# 二叉树的部分内容

---

我们来学习一下二叉树。什么叫二叉树呢？如图

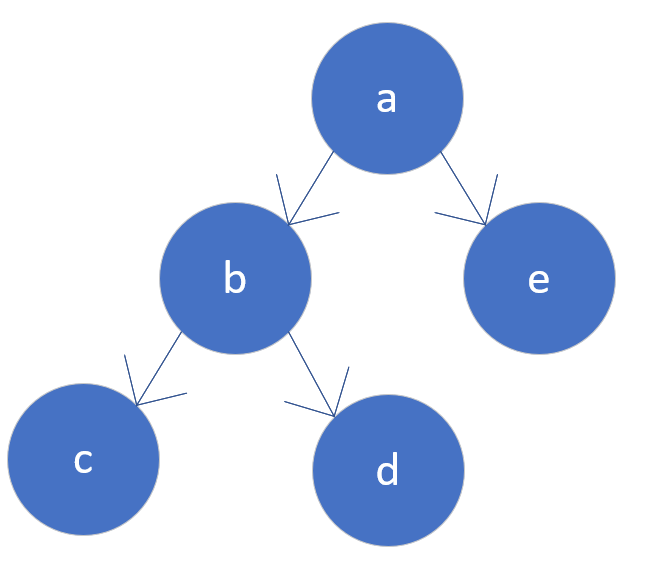
这是一个二叉树的基本类型，那么他的操作有遍历，求高度等

我们主要是介绍遍历操作，还有求高度的操作

遍历分为 递归方式 和 非递归方式

---

下面是源代码

main.cpp

#include"BiTree.h"

int main()
{
	BiTree<char>B1;
	B1.Init();
	B1.Display_Front();
	B1.Disvplay_Middle();
	B1.Display_Last();
	
	std::cout << B1.Deepth() << std::endl;
	return 0;
}
/*
首先初始化，然后前序输出，中序输出，后续输出，最后深度函数
*/

BiTree.h

#pragma once
#ifndef _BITREE_H_
#define _BITREE_H_
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<string>
#include<stack>
#include<cmath>
int max(int a, int b);
template<typename T>
struct node
{
	T data;
	node* LC = nullptr, * RC = nullptr;
};
template<typename T>
class BiTree
{
private:
	node<T>* root = nullptr;//根节点
	node<T>* op1, * op2, * op3;//这是辅助操作指针
	int Node_count;//计算结点的个数
	std::stack<node<T>*>S1;//建立一个栈，空栈
	
	void Create(node<T>*&r);//创建函数
	int Count_High(node<T>*r);//计算高度函数
	void Release(node<T>*base);//释放函数
	//这三个函数用了递归的方式，个人喜好，把他们放进私有中
public:
	BiTree();//初始化
	~BiTree();//当调用结束的时候，自动释放二叉树二叉树
	
	void Init();//创建函数
	int Deepth();//计算深度函数
	void Display_Front();//前序遍历
	void Disvplay_Middle();//中序遍历
	void Display_Last();//后序遍历
};


#endif // !_BITREE_H_

template<typename T>
inline BiTree<T>::BiTree()
{
	root = op1 = op2 = op3 = nullptr;
	Node_count = 0;
	/*
	   初始化指针，使得root，op1，op2，op3为空，结点个数为0
	*/
}

template<typename T>
inline BiTree<T>::~BiTree()
{
	Release(root);
}

template<typename T>
inline void BiTree<T>::Create(node<T>*&r)
{
	/*
		这个函数是利用递归的方式进行创建链表，按照前序的方式创建
		这个函数不可以作为通用函数，只能使用char的形式，因为后面
		的时候判断了字符 # ，故不能作为通用函数
	*/
	using std::cin;
	T data;
	cin.get(data);
	if (data != '\n')
	{
		if (data == '#')//当我碰到 # 字符的时候，就把该指针置成空
			r = nullptr;//然后返回上一层，结束该函数
		else
		{
			Node_count++;//每一次创建的时候，结点值都加一
			r = new node<T>;//如果不是字符 # 的时候，那就申请结点
			r->data = data;//然后赋值
			Create(r->LC);//递归调用Create函数，继续创建左边
			Create(r->RC);//递归调用Create函数，创建右边
		}
	}
}
/*
先序遍历建立二叉树
*/
template<typename T>
inline void BiTree<T>::Init()
{
	Create(root);
}

template<typename T>
inline int BiTree<T>::Count_High(node<T>* r)
{
	//这是一个计算高度的函数，使用了递归的方法
	if (!r)
	{
		/*
		先找到最后一个点，然后返回 0
		*/
		return 0;
	}
	else
	{
		int left = Count_High(r->LC);//用left保存左边返回的值
		int right = Count_High(r->RC);//用right保存右边返回的值
		return 1 + max(left, right);
		//每一次返回，先判断左边的值和右边的值谁大，然后返回大的值加一
	}
}
/*
计算树的高度
思想：从最后一个点开始，然后向上返回计算树的高度
*/
template<typename T>
inline int BiTree<T>::Deepth()
{
	return Count_High(root);
}


template<typename T>
inline void BiTree<T>::Display_Front()
{
	using std::endl;
	using std::cout;
	while (!S1.empty())
		S1.pop();//初始化栈
	op1 = root;
	if (!op1)
	{
		cout << "没有节点" << endl;
	}
	else
	{
		cout << "前序遍历:";
		do
		{
			while (op1)
			{
				S1.push(op1->RC);
				cout << op1->data << " ";
				op1 = op1->LC;
			}
			if (!S1.empty())
			{
				op1 = S1.top();
				S1.pop();				
			}
		} while (!S1.empty()||op1);
		cout << endl;
	}
}
/*
先经历一个点，之后保存该点的右孩子指针到栈中，然后首先找到最左边的位置，然后弹出右孩子
指针，再访问该右孩子，然后在左孩子，依次循环，直到栈为空，退出循环
步骤：Data->Lchild->Rchild
*/
template<typename T>
inline void BiTree<T>::Disvplay_Middle()
{
	using std::endl;
	using std::cout;
	using std::cin;
	while (!S1.empty())
		S1.pop();
	op1 = root;
	cout << "中序遍历:";
	while (op1 || !S1.empty())
	{
		if (op1)
		{
			S1.push(op1);
			op1 = op1->LC;
		}
		else
		{
			op2 = S1.top();
			S1.pop();
			cout << op2->data << " ";
			op1 = op2->RC;
		}
	}
	cout << endl;
}
/*
先访问到该节点，如果指针或者栈不为空，那就执行循环。如果不为空，那就压进栈，然后指针指向左孩子
如果为空了，那就弹出一个，访问该节点，然后指向该孩子的右孩子
步骤: Lchild->Data->Rchild
*/
template<typename T>
inline void BiTree<T>::Display_Last()
{
	using std::endl;
	using std::cout;
	using std::cin;
	while (!S1.empty())
		S1.pop();
	cout << "后续遍历:";
	op1 = root;
	S1.push(op1);

	op3 = nullptr;
	while (op1&&!S1.empty())
	{
		op2 = S1.top();
		if ((!op2->LC && !op2->RC) || op3 && (op3 == op2->LC || op3 == op2->RC))
		{
			cout << op2->data << " ";
			S1.pop();
			op3 = op2;
		}
		else
		{
			if (op2->RC)
				S1.push(op2->RC);
			if (op2->LC)
				S1.push(op2->LC);
		}
	}
	cout << endl;
}
/*
	步骤：Lchild->Rchild->Data
	还没想好怎么说.....
*/


template<typename T>
inline void BiTree<T>::Release(node<T>* base)
{
	if (base)//判断是否到了最后一个位置
	{
		//类似一个后序遍历的方法
		Release(base->LC);//如果没有到达，那就访问左边
		Release(base->RC);//如果没有到达，那就访问右边
		delete base;//然后删除最后一个结点
	}
}

int max(int a, int b)
{
	return a > b ? a : b;
}
/*
	判断最大值的函数
*/

---