BFS 简单思想以及代码
BFS(广搜思想)
广度优先搜索
- 广度优先搜索是图论的搜索算法之一,以下便进行简单叙述
对于每一个顶点来说,都存在着三种颜色
白色,灰色,黑色
而对于每个顶点,都有三种数据类型
颜色类型,前驱或者父节点,路程
分别用:color,u,d来表示
实现思想:
BFS(G , s)
( G 为图,s 为初始点)
struct node
{
collor ; //颜色,包含while, gray, black
d ; //距离
u ; //前驱或者父节点
};
首先,把每一个顶点初始化,其中 u 初始化nullptr,d 初始化为 ∞ ,color 全部初始化为白色
然后把初始点( 起源点 )初始化为
s.color = Gray
s.d = 0
s.u = nullptr ;
然后,使用队列Q。首先初始化队列Q 使得队列Q为空
然后把 s 推进队列Q中,
while(!Q.empty())//当队列非空
{
x = dequere(Q)//取出队头 ,然后让x为队列头,并且在队列中删除这一元素。
//然后在图中的每一个v , v是x的相邻节点进行循环
for( each v ∈ G.Adj[ x ] )//Adj是相邻点的意思
{
if( v.color == white )
{
v.color = gray//把点涂灰
v.d=x.d+1
v.u=x;
enqueue( Q, v )//把v放进刚刚的队列中
}
}
x.color= black//把点涂黑
}
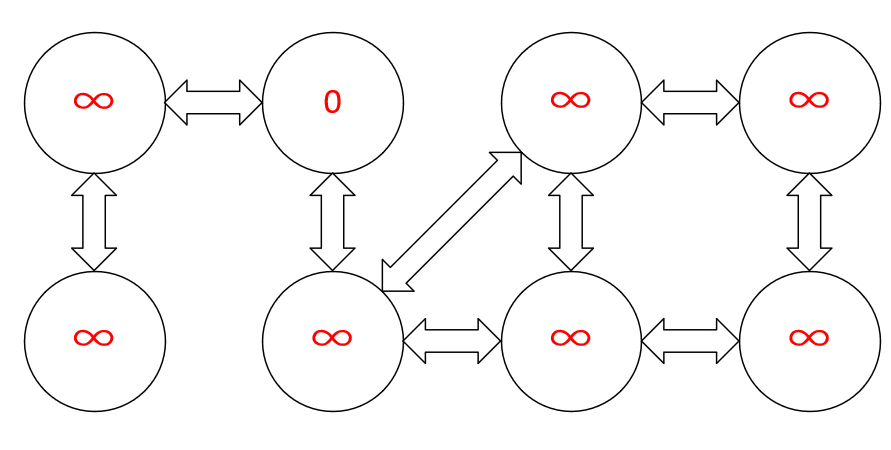
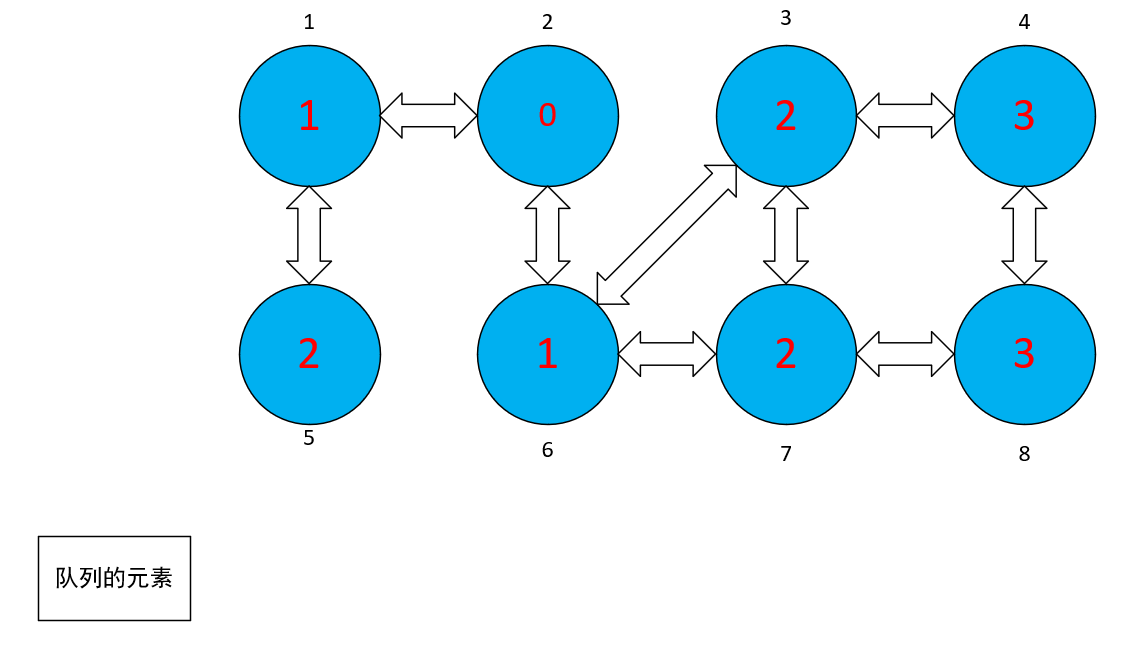
下面是图示样例:
以下有部分差异信息
白色=白色 灰色=黄色 黑色=蓝色
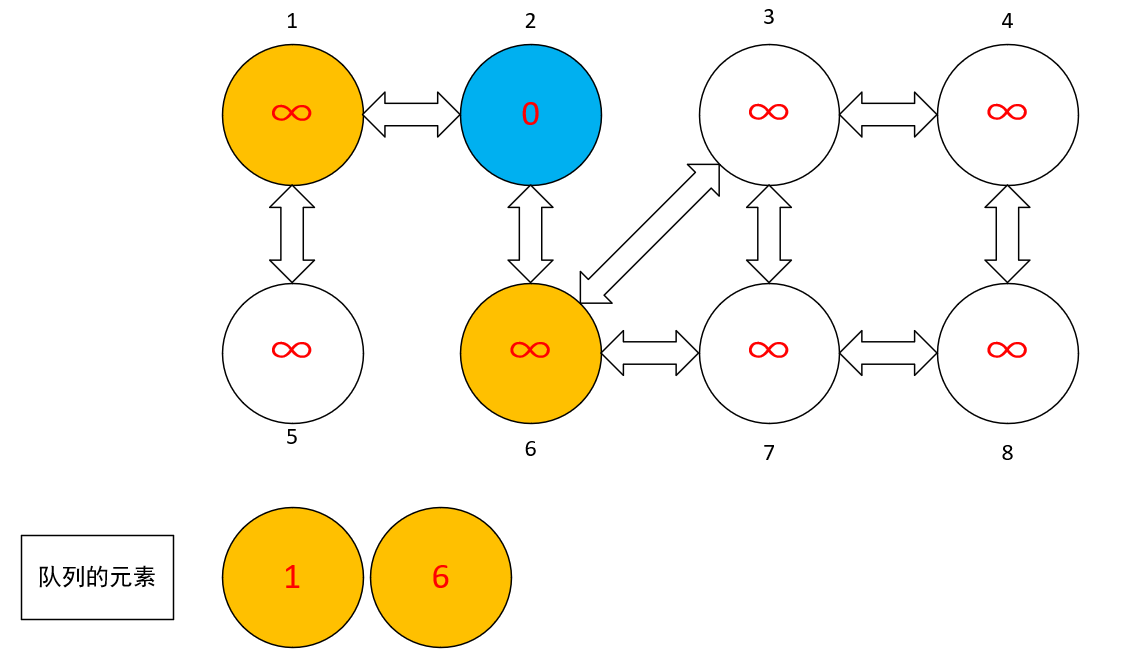
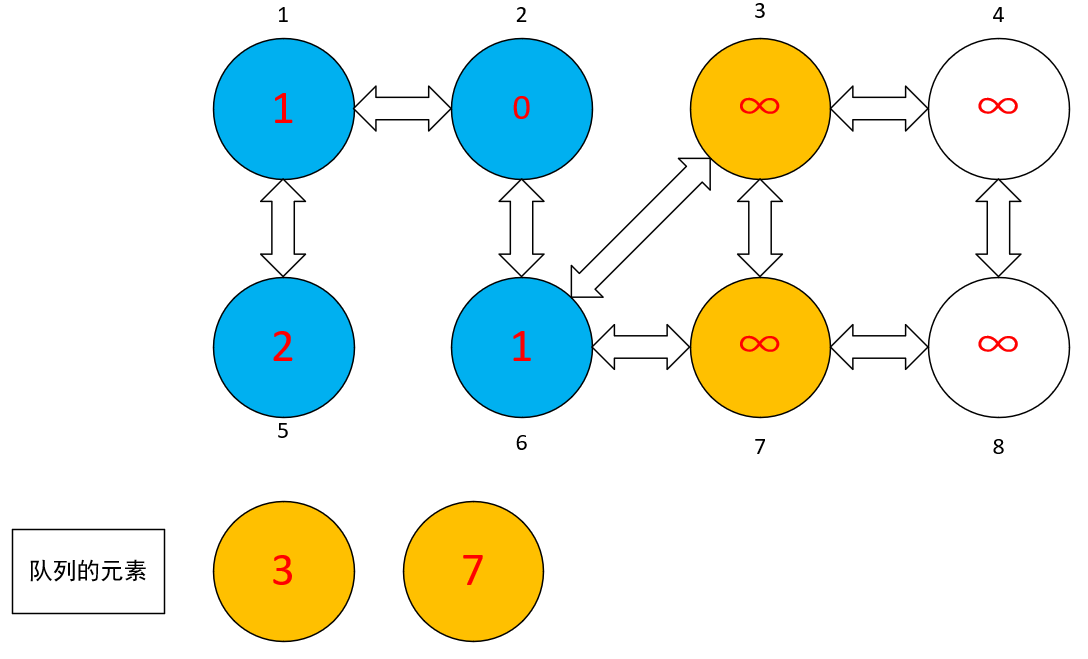
- 首先我们选择 ② 点开始,② 作为起源点,首先把 ② 点标记为黄色然后根据算法步骤,把 ② 点放进队列中,然后判断队列是否为空。此时不为空,那么就把队列的头弹出,并且寻找此结点对应的相邻结点。
- 当找到相邻结点的时候,把相邻节点标记为黄色,把队列中弹出的头结点标记为蓝色。然后把对应的一结点和六结点标记成黄色,并且放进队列中。
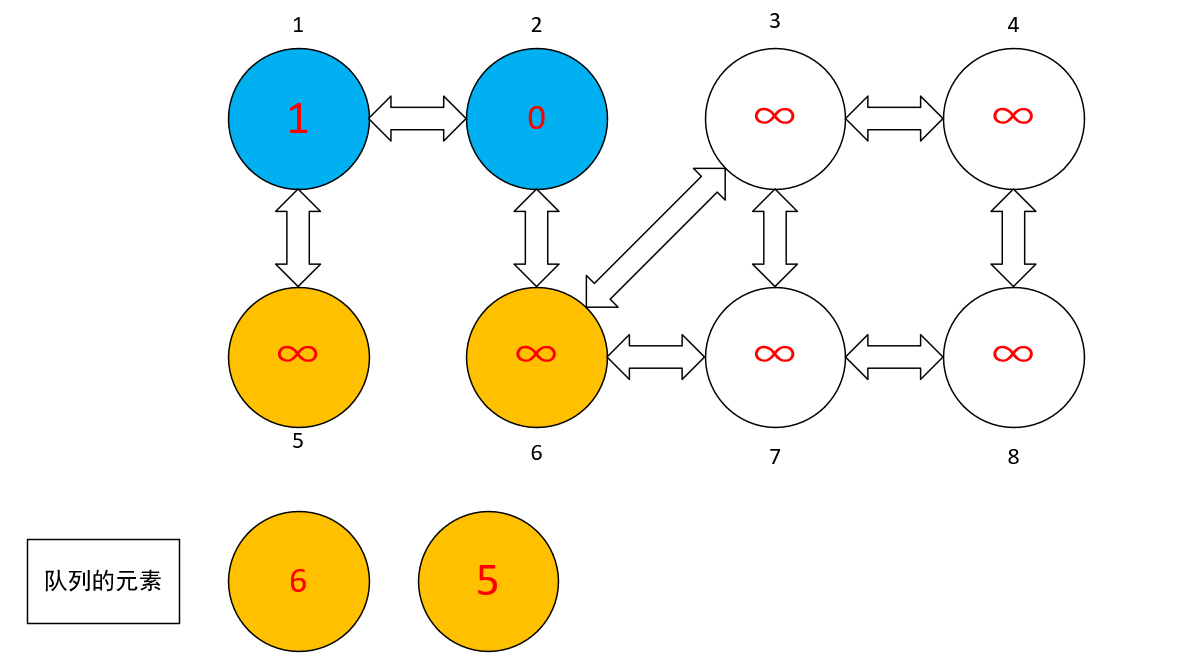
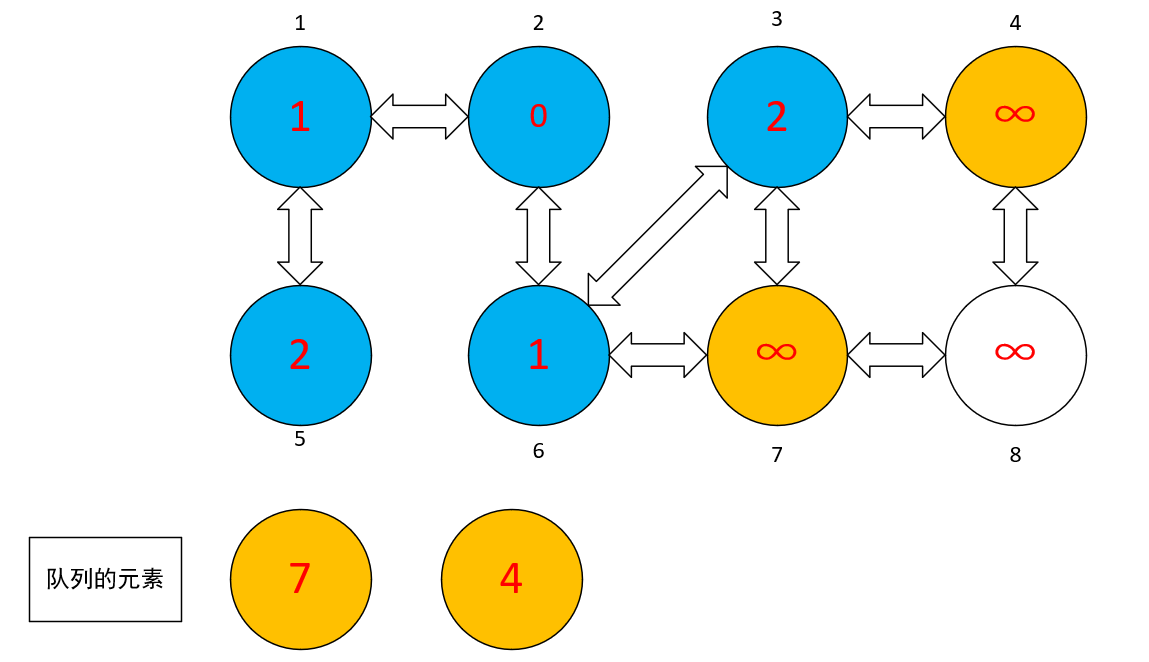
- 此时从队列中弹出 ① 结点,然后把 ① 结点标记成为蓝色,然后把 ① 结点标记为蓝色,把与 ① 结点相邻的结点标记为黄色,然后放进队列中
- 同理,从队列中的头弹出一个元素,然后标记其相邻结点,再把其相邻结点涂成黄色,把其自身涂成蓝色,然后把相邻结点推进队列中,并且上一头元素
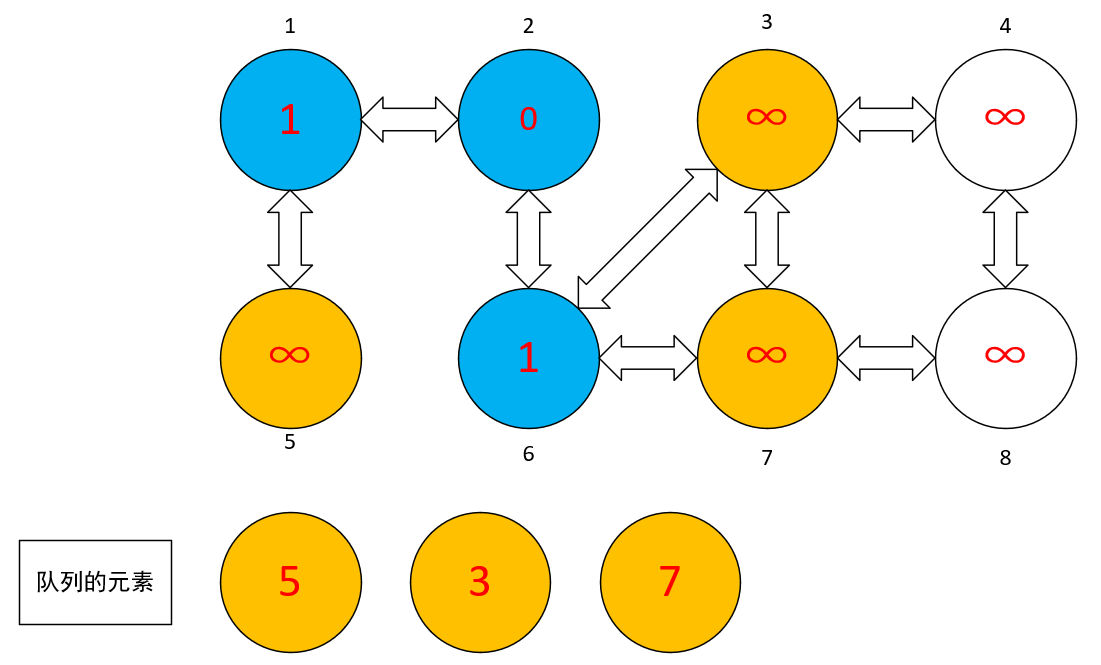
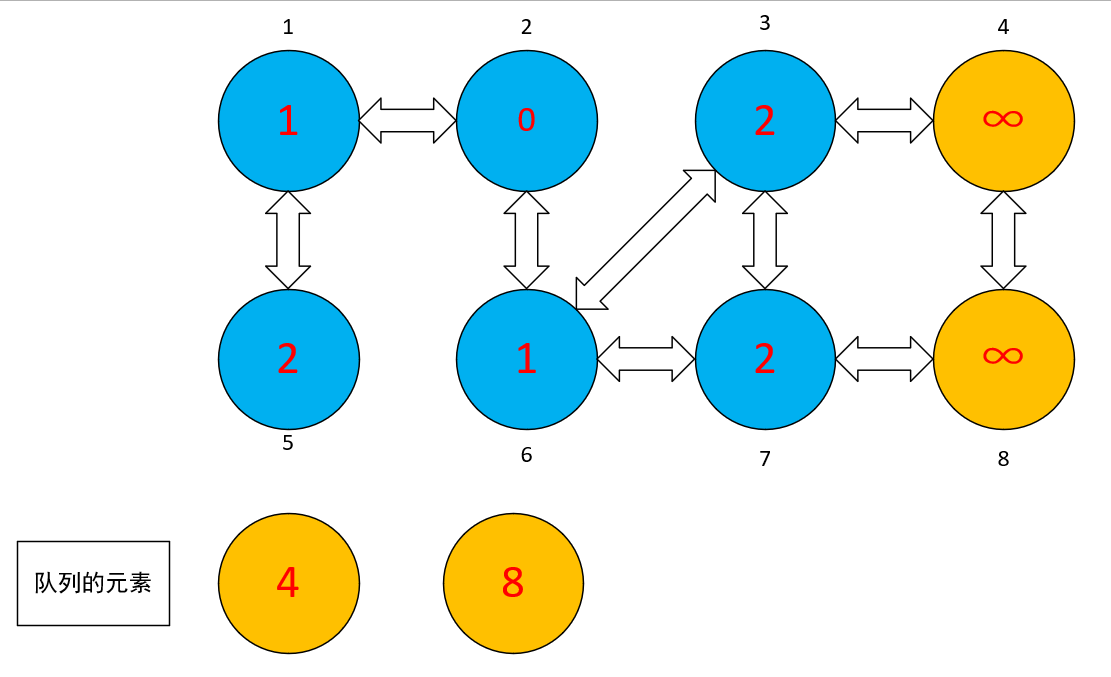
- 依次弹出,③,⑦,然后依次把相邻结点推进队列中。然后分别标记③,⑦的相邻结点,然后继续进行下去
- 到③被标记为蓝色的时候,去找③对应的相邻结点,找到了④,⑦。然而⑦已经在队列中了,说明⑦有其相对应的前驱结点,故不用标记⑦结点。由于⑦是在⑥标记的时候,与⑥的相邻结点,因此,⑦的前驱为⑥。此时,在队列中弹出的时候,其 d 值为其前驱结点中的 d 值加一而得。
随后,把⑦标记为蓝色,标记对应相邻结点,从而使前驱为该节点。然后进行类似上面的操作。
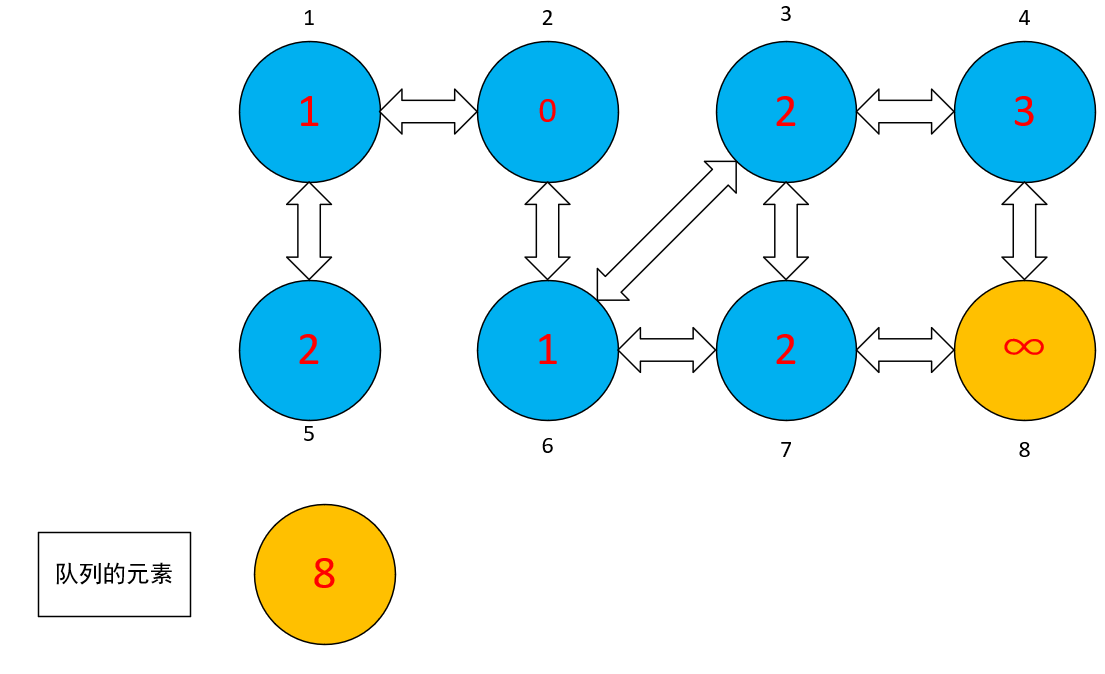
- 直到所有的点都遍历完成,都标记为相对应的蓝色。此时队列为空。每一个点中都有从②号结点出发,到该结点的距离。
实现代码如下
#include<iostream>
#include<cstdlib>
#include<vector>
#include<string>
#include<queue>
using namespace std;
struct Point
{
int dis=0;
string color="white";
Point* pre = nullptr;
};
void BFS(vector<vector<bool>>& if_arrive, vector<Point>&pos, int start, int n);
void Display_distance(vector<Point>& pos, int start);
int main()
{
int n;
int a, b;
int start;
cout << "请输入有几个顶点" << endl;
cin >> n;
vector<Point>pos(n);//点的位置以及前驱
//申请二维空间
vector <vector<bool>> if_arrive(n);
for (int i = 0; i < n; i++)
if_arrive[i].resize(n);
cout << "请输入各个点之间的关系,(0,0)退出" << endl;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if_arrive[i][j] = false;
//初始化
while (cin >> a >> b && (a != 0 || b != 0))
if_arrive[a - 1][b - 1] = true;
cout << "请输入开始点" << endl;
cin >> start;
BFS(if_arrive, pos, start, n);//进行广搜
Display_distance(pos, start);//进行显示距离
//内存清理
for (int i = 0; i < n; i++)
if_arrive[i].clear();
if_arrive.clear();
pos.clear();
return 0;
}
void BFS(vector<vector<bool>>& if_arrive, vector<Point>&pos, int start,int n)
{
int sit;
queue<int> Q;
start--;
pos[start].color = "black";//把源结点标记为黑色
pos[start].pre = nullptr;//源结点前驱为空
for (int i = 0; i < n; i++)
if (if_arrive[start][i] == true)//如果存在该路径
{
Q.push(i);//进队
pos[i].color = "gray";//相邻为灰色
pos[i].pre = &pos[start];
pos[i].dis++;
}
while (!Q.empty())//队列非空
{
sit = Q.front();//取头
Q.pop();//出队
for (int i = 0; i < n; i++)
{
if (if_arrive[sit][i] == true && pos[i].color == "white")
{
pos[i].color = "gray";//找到相邻的,先变颜色
pos[i].pre = &pos[sit];//然后前驱指向
pos[i].dis = pos[sit].dis+1;//然后距离加一
Q.push(i);//把i排进队列中
}
}
pos[sit].color = "black";//刚刚队列中的头的颜色标记为黑色
}
}
void Display_distance(vector<Point>&pos,int start)
{
vector<Point>::iterator iter;
int i = 1;
cout << "从第 " << start << " 点开始到各个点的距离" << endl;
for (iter = pos.begin(); iter < pos.end(); iter++, i++)
cout << "到第 " << i << " 个点的距离" << iter->dis << endl;
cout << endl;
}
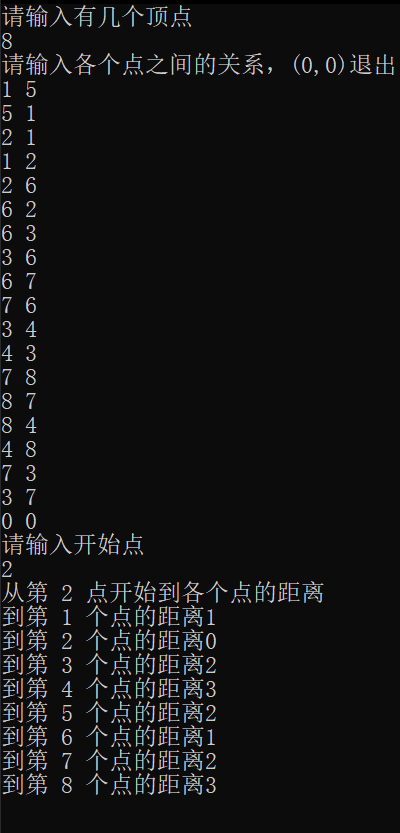
程序运行结果如下
借鉴 《算法导论》 一书
这是小睿的博客,如果需要转载,请标注出处啦~ヾ(≧▽≦*)o谢谢。