Codeforces-687A NP-Hard Problem

Recently, Pari and Arya did some research about NP-Hard problems and they found the minimum vertex cover problem very interesting.

Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edge uv there is at least one endpoint of it in this set, i.e. 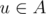 or  (or both).

Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.

They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A and B, such that both A and B are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).

Input

The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.

Each of the next m lines contains a pair of integers ui and vi (1  ≤  ui,  vi  ≤  n), denoting an undirected edge between ui and vi. It's guaranteed the graph won't contain any self-loops or multiple edges.

Output

If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).

If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integer k denoting the number of vertices in that vertex cover, and the second line contains kintegers — the indices of vertices. Note that because of m ≥ 1, vertex cover cannot be empty.

Examples

input

4 2
1 2
2 3

output

1
2 
2
1 3 

input

3 3
1 2
2 3
1 3

output

-1

Note

In the first sample, you can give the vertex number 2 to Arya and vertices numbered 1 and 3 to Pari and keep vertex number 4 for yourself (or give it someone, if you wish).

In the second sample, there is no way to satisfy both Pari and Arya.

题目大意：

给你一个图，保证没有自环和重边，让你求两个互斥的子集，这两个子集都可以构成这幅图的一个覆盖。

解法：

其实看起来很像二部图= =所以只需要染个色就可以了。然后输出就行。上代码

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 5;
vector<int> G[maxn], a, b;
int n, m, flag;
int col[maxn];

bool bfs(int s) {  
    queue<int> p;  
    p.push(s);  
    col[s] = 1;  
    while(!p.empty()) {  
        int from = p.front();  
        p.pop();  
        
        int len = G[from].size();
        for(int i = 0; i < len; ++i) { 
        	int v = G[from][i];
            if(col[v] == -1) {  
                p.push(v);
                col[v] = !col[from];
            }  
            if(col[from] == col[v])
                return false;  
        }  
    }  
    return true;       
}  
int main()
{
	scanf("%d%d", &n, &m);
	a.clear(); b.clear();
	for(int i = 0; i <= n; ++i) G[i].clear();
	for(int i = 0; i < m; ++i){
		int u, v;
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	
	flag = 0;
	memset(col, -1, sizeof(col));
	for(int i = 1; i <= n; i++)
        if(col[i] == -1 && !bfs(i)) {
            flag = true;  
            break;    
        }  
	if(flag){
		puts("-1");
	}else{
		for(int i = 1; i <= n; ++i){
			if(G[i].size() == 0) col[i] = -1;
			if(col[i] == 0){
				a.push_back(i);
			}else if(col[i] == 1){
				b.push_back(i);
			}
		}
		
		int len = a.size();
		printf("%d\n", len);
		for(int i = 0; i < len; ++i){
			if(i) printf(" ");
			printf("%d", a[i]);
		}
		len = b.size();
		printf("\n%d\n", len);
		for(int i = 0; i < len; ++i){
			if(i) printf(" ");
			printf("%d", b[i]);
		}
		puts("");
	}
	return 0;
}