POJ-1324 Holedox Moving

Description

During winter, the most hungry and severe time, Holedox sleeps in its lair. When spring comes, Holedox wakes up, moves to the exit of its lair, comes out, and begins its new life. 
Holedox is a special snake, but its body is not very long. Its lair is like a maze and can be imagined as a rectangle with n*m squares. Each square is either a stone or a vacant place, and only vacant places allow Holedox to move in. Using ordered pair of row and column number of the lair, the square of exit located at (1,1). 

Holedox's body, whose length is L, can be represented block by block. And let B1(r1,c1) B2(r2,c2) .. BL(rL,cL) denote its L length body, where Bi is adjacent to Bi+1 in the lair for 1 <= i <=L-1, and B1 is its head, BL is its tail. 

To move in the lair, Holedox chooses an adjacent vacant square of its head, which is neither a stone nor occupied by its body. Then it moves the head into the vacant square, and at the same time, each other block of its body is moved into the square occupied by the corresponding previous block. 

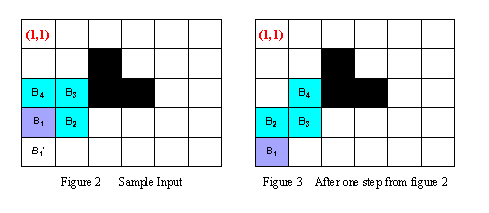
For example, in the Figure 2, at the beginning the body of Holedox can be represented as B1(4,1) B2(4,2) B3(3,2)B4(3,1). During the next step, observing that B1'(5,1) is the only square that the head can be moved into, Holedox moves its head into B1'(5,1), then moves B2 into B1, B3 into B2, and B4 into B3. Thus after one step, the body of Holedox locates in B1(5,1)B2(4,1)B3(4,2) B4(3,2) (see the Figure 3). 

Given the map of the lair and the original location of each block of Holedox's body, your task is to write a program to tell the minimal number of steps that Holedox has to take to move its head to reach the square of exit (1,1). 

Input

The input consists of several test cases. The first line of each case contains three integers n, m (1<=n, m<=20) and L (2<=L<=8), representing the number of rows in the lair, the number of columns in the lair and the body length of Holedox, respectively. The next L lines contain a pair of row and column number each, indicating the original position of each block of Holedox's body, from B1(r1,c1) to BL(rL,cL) orderly, where 1<=ri<=n, and 1<=ci<=m,1<=i<=L. The next line contains an integer K, representing the number of squares of stones in the lair. The following K lines contain a pair of row and column number each, indicating the location of each square of stone. Then a blank line follows to separate the cases. 

The input is terminated by a line with three zeros. 

Note: Bi is always adjacent to Bi+1 (1<=i<=L-1) and exit square (1,1) will never be a stone. 

Output

For each test case output one line containing the test case number followed by the minimal number of steps Holedox has to take. "-1" means no solution for that case.

Sample Input

5 6 4
4 1
4 2
3 2
3 1
3
2 3
3 3
3 4

4 4 4
2 3
1 3
1 4
2 4
4

2 1
2 2
3 4
4 2

0 0 0

Sample Output

Case 1: 9
Case 2: -1

Hint

In the above sample case, the head of Holedox can follows (4,1)->(5,1)->(5,2)->(5,3)->(4,3)->(4,2)->(4,1)->(3,1)->(2,1)->(1,1) to reach the square of exit with minimal number of step, which is nine. 

题目大意：

一个蛇，长度为l，要爬到(1,1)点，问你最短的路径是多少。如果不存在最短路径就输出-1

解题思路：

BFS+哈希（状态压缩BFS）

将蛇的身体当做状态，记录蛇头位置，然后以蛇头位置开始，向后面计算。

比如说第一个样例。

我们约定(0,1)为状态00，(1,0)为状态01，(0,-1)为状态10，(-1,0)为状态11，注意这个部分与后面运算的过程要一一对应

蛇头位置为(4,1)记录下来，然后考虑第二个位置(4,2)，发现两者差别为(0,1)，所以状态为00，第三个位置(3,2)，与第二个位置差距为(-1,0)，所以状态为11，第四个位置(3,1)，与第三个位置差距为(0,-1)，所以状态为10

那么把这三个状态组合在一起，就成为状态101100，同样的也可以轻松的按照这个把状态还原为蛇的位置。

判断这个题目只需要考虑是否满足蛇的下个位置1.不会与当前身体的任何部分相碰撞，2.没有另外一个相同的状态在下个蛇头的位置出现过。

在满足这两个条件之后，就可以得到最后的结果了。

代码：

#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;

typedef pair<int, int> pi;
typedef struct node{
    int x, y;
    int st;
    node(){}
    node(int a, int b, int status){
        x = a; y = b;
        st = status;
    }
}Snake;

const int maxn = 21;
const int dir[4][2] = {0,1, 1,0, 0,-1, -1,0};

int n, m, l;
int g[maxn][maxn], vis[maxn][maxn][1<<14];

bool Judge(Snake p, int t){
    int a, b, nx, ny, flag;
    int row, col;
    row = p.x + dir[t][0];
    col = p.y + dir[t][1];
    
    a = p.x; b = p.y;
    
    if(row == a && col == b) return false;
    int k = l - 1;
    while(k--){
        int q = p.st & 3;
        p.st >>= 2;
        
        nx = a + dir[q][0];
        ny = b + dir[q][1];
        
        if(nx == row && ny == col) return false;
        a = nx; b = ny;
    }
    return true;
}
void bfs(Snake s){
    Snake p, tmp;
    queue<Snake> q;
    while(!q.empty()) q.pop();
    memset(vis, 0, sizeof(vis));
    
    q.push(s);
    vis[s.x][s.y][s.st] = 1;
    
    while(!q.empty()){
        p = q.front();
        q.pop();
        
        if(p.x == 1 && p.y == 1){
            printf("%d\n", vis[p.x][p.y][p.st] - 1);
            return;
        }
        
        for(int i = 0; i < 4; ++i){
            int nx = p.x + dir[i][0];
            int ny = p.y + dir[i][1];
            tmp = node(nx, ny, p.st);
            
            tmp.st = tmp.st & ((1 << (2 * (l - 2))) - 1);
            tmp.st <<= 2;
            tmp.st |= (i + 2) % 4;
            
            if(nx >= 1 && ny >= 1 && nx <= n && ny <= m && !vis[tmp.x][tmp.y][tmp.st] && !g[nx][ny] && Judge(p, i)){
                vis[nx][ny][tmp.st] = vis[p.x][p.y][p.st] + 1;
                q.push(tmp);
            }
        }
    }
    puts("-1");
}
int main()
{
    // freopen("test.in", "r+", stdin);
    // freopen("test.out", "w+", stdout);
    
    int cas = 1;
    int a, b, k, tmp1, tmp2;
    while(~scanf("%d%d%d", &n, &m, &l)){
        if(n == 0 && m == 0 && l == 0) break;
        
        Snake ss;
        for(int i = 0; i < l; ++i){
            scanf("%d%d", &a, &b);
            
            if(i == 0) ss = node(a, b, 0);
            else{
                for(int j = 0; j < 4; ++j){
                    int nx = tmp1 + dir[j][0];
                    int ny = tmp2 + dir[j][1];
                    
                    if(nx == a && ny == b){
                        ss.st |= j << (2 * (i - 1));
                        break;
                    }
                }
            }
            tmp1 = a; tmp2 = b;
        }

        scanf("%d", &k);
        memset(g, 0, sizeof(g));
        for(int i = 0; i < k; ++i){
            scanf("%d%d", &a, &b);
            g[a][b] = 1;
        }
        
        printf("Case %d: ", cas);
        bfs(ss);
        ++cas;
    }
    return 0;
}