POJ-2935 Basic Wall Maze
Description
In this problem you have to solve a very simple maze consisting of:
- a 6 by 6 grid of unit squares
- 3 walls of length between 1 and 6 which are placed either horizontally or vertically to separate squares
- one start and one end marker
A maze may look like this:
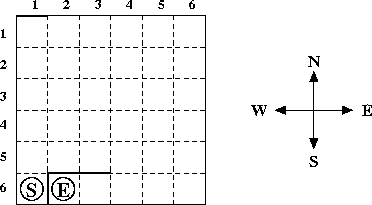
You have to find a shortest path between the square with the start marker and the square with the end marker. Only moves between adjacent grid squares are allowed; adjacent means that the grid squares share an edge and are not separated by a wall. It is not allowed to leave the grid.
Input
The input consists of several test cases. Each test case consists of five lines: The first line contains the column and row number of the square with the start marker, the second line the column and row number of the square with the end marker. The third, fourth and fifth lines specify the locations of the three walls. The location of a wall is specified by either the position of its left end point followed by the position of its right end point (in case of a horizontal wall) or the position of its upper end point followed by the position of its lower end point (in case of a vertical wall). The position of a wall end point is given as the distance from the left side of the grid followed by the distance from the upper side of the grid.
You may assume that the three walls don’t intersect with each other, although they may touch at some grid corner, and that the wall endpoints are on the grid. Moreover, there will always be a valid path from the start marker to the end marker. Note that the sample input specifies the maze from the picture above.
The last test case is followed by a line containing two zeros.
Output
For each test case print a description of a shortest path from the start marker to the end marker. The description should specify the direction of every move (‘N’ for up, ‘E’ for right, ‘S’ for down and ‘W’ for left).
There can be more than one shortest path, in this case you can print any of them.
Sample Input
1 6 2 6 0 0 1 0 1 5 1 6 1 5 3 5 0 0
Sample Output
NEEESWW
题目大意:
有一个6*6的迷宫,有三堵墙。给出每堵墙的起点和终点以及起点和终点,问你从起点到终点的最短路径,并输出。
解题思路:
这个题目与基础的BFS迷宫题目的一个区别在于不再用点矩阵来表示迷宫而是用一个个小方块来表示迷宫。但是本质还是相同的,只要建好图就可以了。
代码:
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 8;
const char pri[4] = {'N', 'E', 'S', 'W'};
const int dir[4][2] = {-1,0, 0,1, 1,0, 0,-1};
typedef struct point{
int x, y;
point(){}
point(int a, int b){x = a; y = b;}
}Coord;
typedef struct node{
int x, y;
bool to[4];
node(int a = 0, int b = 0){
x = a; y = b;
to[0] = to[1] = to[2] = to[3] = 0;
}
}Maze;
Maze m[maxn][maxn];
int sx, sy, ex, ey;
int vis[maxn][maxn];
Coord pre[maxn][maxn];
void Print(int row, int col){
if(row == -1 && col == -1) return;
Print(pre[row][col].x, pre[row][col].y);
int nx, ny;
for(int i = 0; i < 4; ++i){
nx = pre[row][col].x + dir[i][0];
ny = pre[row][col].y + dir[i][1];
if(nx == row && ny == col){
printf("%c", pri[i]);
break;
}
}
}
void bfs(){
queue<Maze> q;
while(!q.empty()) q.pop();
memset(vis, 0, sizeof(vis));
memset(pre, -1, sizeof(pre));
vis[sy][sx] = 1;
q.push(m[sy][sx]);
while(!q.empty()){
Maze p = q.front();
q.pop();
if(p.x == ey && p.y == ex){
Print(ey, ex); puts("");
return;
}
for(int i = 0; i < 4; ++i){
int nx = p.x + dir[i][0];
int ny = p.y + dir[i][1];
if(!p.to[i] && nx >= 1 && nx <= 6 && ny >= 1 && ny <= 6 && !vis[nx][ny]){
vis[nx][ny] = 1;
q.push(m[nx][ny]);
pre[nx][ny] = point(p.x, p.y);
}
}
}
}
int main()
{
// freopen("test.in", "r+", stdin);
// freopen("test.out", "w+", stdout);
int ax, ay, bx, by;
while(~scanf("%d%d", &sx, &sy)){
if(sx == 0 && sy == 0) break;
scanf("%d%d", &ex, &ey);
for(int i = 1; i <= 6; ++i){
for(int j = 1; j <= 6; ++j){
m[i][j] = node(i, j);
}
}
for(int i = 0; i < 3; ++i){
scanf("%d%d%d%d", &ax, &ay, &bx, &by);
if(ax == bx){
for(int i = min(ay, by) + 1; i <= max(ay, by); ++i){
if(ax == 0){
m[i][1].to[3] = 1;
}else if(ax == 6){
m[i][6].to[1] = 1;
}else{
m[i][ax].to[1] = m[i][ax+1].to[3] = 1;
}
}
}else{
for(int i = min(ax, bx) + 1; i <= max(ax, bx); ++i){
if(ay == 0){
m[1][i].to[0] = 1;
}else if(ay == 6){
m[6][i].to[2] = 1;
}else{
m[ay][i].to[2] = m[ay+1][i].to[0] = 1;
}
}
}
}
bfs();
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号