2015 XDU 校赛网络赛

问题 A: IP查询

时间限制: 1 Sec  内存限制: 128 MB
提交: 3374  解决: 204
[提交][状态][讨论版]

题目描述

现实生活中，每一个IP段都指向一座城市。为了简化问题，我们将IP段直接看做一个整形数，每座城市也有自己的唯一标识ID,也可以看做一个整数。那么问题来了，现在已知有多个闭区间代表多个IP段，每个区间对应一个城市的ID。现在，小L要查询某个IP属于那个城市，希望聪明的你来帮他完成。

 

输入

第一行输入T,表示有T组测试数据（T<=5)
接下来一行输入整数n,代表有n个区间（0=<n<=10^5）
接下来n行，每行输入三个整数x,y,id.代表区间[x,y]所对应的城市ID。数据确保任意俩个区间交集为空，且ID唯一。（0=<x<y<=10^8 , 0=<ID<=10^8）
接下来一行输入整数m,代表m次查询（0=<m<=10^5）
接下来m行，每行输入一个整数V，代表所查询的IP（V<=10^8）

 

输出

对于每次查询，输出一行，表示其对应的城市ID。
如果未找到，输出-1

 

样例输入

1
2
3 5 99
1 2 77
3
1
3
9

样例输出

77
99
-1 


题目大意：
　　就是说，给你n个区间和m个询问，然后，每次询问一个数字，看他是不是落在了[l_i,r_i]的区间中。。。
解题思路：
　　直接给每个区间标号，然后二分就行了。。。二分到有标号的区间，我们就输出区间的ip，没有的话，我们就给个-1.
 1 # include<cstdio>
 2 # include<iostream>
 3 # include<algorithm>
 4  
 5 using namespace std;
 6  
 7 # define MAX 100000+4
 8  
 9 struct node
10 {
11     int left,right;
12     int ip;
13 }a[MAX];
14  
15 int n;
16  
17 int cmp ( const struct node & aa,const struct node & bb )
18 {
19     return aa.left < bb.left;
20 }
21  
22 int bsearch ( int val )
23 {
24     int hi = n;
25     int lo = 1;
26     while ( lo <= hi )
27     {
28         int mid = (lo+hi)>>1;
29        // cout<<"mid="<<mid<<endl;
30         if ( val >= a[mid].left&&val <= a[mid].right )
31         {
32             return a[mid].ip;
33         }
34         else if ( a[mid].left > val )
35         {
36             hi = mid-1;
37         }
38         else if ( a[mid].right < val )
39         {
40             lo = mid+1;
41         }
42     }
43     return -1;
44 }
45  
46  
47 int main(void)
48 {
49     int t;scanf("%d",&t);
50     while ( t-- )
51     {
52         int ans = 0;
53         scanf("%d",&n);
54         for ( int i = 1;i <= n;i++ )
55         {
56             scanf("%d%d%d",&a[i].left,&a[i].right,&a[i].ip);
57         }
58         sort(a+1,a+n+1,cmp);
59         int m;scanf("%d",&m);
60         while ( m-- )
61         {
62             int t;scanf("%d",&t);
63             ans = bsearch(t);
64             printf("%d\n",ans);
65  
66         }
67  
68     }
69  
70  
71     return 0;
72 }

 

问题 B: 简单逆序对

时间限制: 1 Sec  内存限制: 128 MB
提交: 2611  解决: 374
[提交][状态][讨论版]

题目描述

逆序对问题对于大家来说已经是非常熟悉的问题了，就是求i<j时，a[i] > a[j]的组数。现在请你求出一串数字中的逆序对的个数，需要注意的是，这些数字均在[0,9]之内。

 

输入

第一行输入T,表示有T组测试数据
对于每组数据，首先输入n,代表有n个数(0<n<=10^6)
接下来输入n个数，每个数都在[0,9]之内

 

输出

输出逆序对的个数，且对10^9+7取模

 

样例输入

2
3
3 2 1
3
1 2 1

样例输出

3
1


解题思路：
　　一开始用bit直接跑，没错，果断直接T了，原因很简单lowbit==0的时候我没有考虑进去。最后看了下数据只有[0,9]果断的跑了暴力（10^6*10）
每次扫一遍，记录这个数字前面有多少个数字比他大。

代码：
 1 # include<cstdio>
 2 # include<iostream>
 3 # include<cstring>
 4  
 5 using namespace std;
 6  
 7 # define MAX 1000004
 8 # define MOD 1000000007
 9  
10 typedef long long LL;
11  
12 int a[MAX];
13 int cnt[MAX];
14  
15 int main(void)
16 {
17     int t;scanf("%d",&t);
18     while ( t-- )
19     {
20         int n;scanf("%d",&n);
21         for ( int i = 0;i < n;i++ )
22         {
23             scanf("%d",&a[i]);
24         }
25         LL ans = 0;
26         for ( int i = 0;i < n;i++ )
27         {
28             for ( int j = a[i]+1;j < 10;j++ )
29             {
30                 ans+=(cnt[j]%MOD);
31             }
32             cnt[a[i]]++;
33         }
34         printf("%d\n",ans%MOD);
35         memset(cnt,0,sizeof(cnt));
36     }
37  
38  
39     return 0;
40 }

 

问题 D: 修理OJ

时间限制: 1 Sec  内存限制: 128 MB
提交: 2702  解决: 633
[提交][状态][讨论版]

题目描述

Boooooom！XDOJ坏掉了！经分析，XDOJ坏掉和一个表达式runid mod oj_tot有关（mod表示取余数，例如10 mod 3=1，5 mod 1=0）。

由于runid可能很大，它被表示成ab的形式。

由于xry111前一天CF打得太晚，现在他完全傻逼了，算不出这个表达式的值。请你写一个程序计算这个值。

数据范围：1<=a, b, oj_tot<=1000

 

输入

多组数据（不超过1000组），每组数据1行，包括3个整数a、b、oj_tot。

 

输出

输出一行，包含一个整数ab mod oj_tot。

 

样例输入

2 4 100
3 3 3

样例输出

16
0


解题思路：
　　直接快速幂取模就OK了。。打个板子上去。

代码：
 1 # include<cstdio>
 2 # include<iostream>
 3  
 4 using namespace std;
 5  
 6 typedef long long LL;
 7  
 8 int a,b,c;
 9  
10 int PowerMod( int a,int b,int c )
11 {
12     int ans = 1;
13     a%=c;
14     while ( b > 0 )
15     {
16         if ( b&1 )
17         {
18             ans = ( ans*a)%c;
19         }
20         b/=2;
21         a = (a*a)%c;
22     }
23     return ans;
24 }
25  
26  
27 int main(void)
28 {
29     while ( scanf("%d%d%d",&a,&b,&c)!=EOF )
30     {
31         LL res = PowerMod( a,b,c);
32         printf("%lld\n",res);
33     }
34  
35     return 0;
36 }

 





问题 F: 数字工程

时间限制: 1 Sec  内存限制: 128 MB
提交: 954  解决: 122
[提交][状态][讨论版]


题目描述




ACM实验室开启了一个数字工程项目，希望把正整数n通过一些特殊方法变成1。


可采用的方法有：（1）减去1；（2）除以它的任意一个素因子。 每操作一次消耗一个单位的能量。


问，把n变成1最少需要消耗多少能量？


 






输入




多组测试


对于每组测试，输入正整数n (1<=n<=1,000,000)


 






输出




输出最少消耗的能量


 






样例输入


1
4


样例输出


0
2


提示


解题思路：
　　dp来搞，用dp[i]表示把数字i变成1所需要的最小花费，那么我们写出一个状态转移方程dp[i] = min(dp[i-1],dp[k/prime])+1,把1-1000000内的素数都打出来，然后一个一个除就可以了。

代码：




 1 # include<cstdio>
 2 # include<iostream>
 3 
 4 using namespace std;
 5 
 6 # define inf 99999999
 7 # define MAX 1000000+4
 8 
 9 
10 int len;
11 int dp[MAX];
12 int prime[MAX];
13 int book[MAX];
14 
15 
16 void init()
17 {
18     for ( int i = 2;i < MAX;i++ )
19     {
20         book[i] = 1;
21     }
22     for ( int i = 2;i < MAX;i++ )
23     {
24         if ( book[i]==1 )
25         {
26             for ( int j = 2*i;j < MAX;j+=i )
27             {
28                 book[j] = 0;
29             }
30         }
31     }
32     len = 0;
33     for ( int i = 2;i < MAX;i++ )
34     {
35         if ( book[i]==1 )
36         {
37             prime[len++] = i;
38         }
39     }
40     for ( int i = 1;i < MAX;i++ )
41         dp[i] = inf;
42     dp[1] = 0;
43     for ( int i = 1;i < MAX;i++ )
44     {
45         for  ( int j = 0;j < len;j++ )
46         {
47             long long t = (long long )i*prime[j];
48             if ( t>MAX )
49                 break;
50             dp[t] = min(dp[t],dp[i]+1);
51         }
52         dp[i+1] = min(dp[i+1],dp[i]+1);
53     }
54 }
55 
56 
57 int main(void)
58 {
59     int n;
60     init();
61     while ( scanf("%d",&n)==1 )
62     {
63         printf("%d\n",dp[n]);
64     }
65 
66     return 0;
67 }




 




1027: Feibonaqi数列

时间限制: 1 Sec  内存限制: 128 MB
提交: 2048  解决: 274
[提交][状态][讨论版]


题目描述




北雷老中医不懂 Fibonacci，于是他定义了一种名叫Feibonaqi的数列，数列满足以下要求：
1.f(0)=0,f(1)=1
2.f(n)=2f(n-1)+f(n-2),n>1
那么问题来了，这个数列的第n项是多少呢？
（不为难大家用高精度了，你只需要将结果对1,000,000,007取模后输出即可）


 





输入




多组数据
每组数据一行，包含一个整数n，1<n<1,000,000,000


 





输出




每组数据输出一个整数，即为f(n)对1,000,000,007取模后的结果


 





样例输入


2
3
4


样例输出


2
5
12



解题思路：


矩阵乘法+空间换时间(减少乘法，取模运算)


 　　数列的递推公式为：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)


　　 用矩阵表示为：




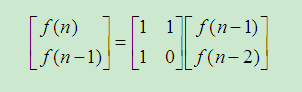
　　进一步，可以得出直接推导公式：




 　　由于矩阵乘法满足结合律，在程序中可以事先给定矩阵的64，32，16，8，4，2，1次方，加快程序的执行时间。（有些题目需要取模运算，也可以事先进行一下）。给定的矩阵次幂，与二进制有关是因为，如下的公式存在解，满足Xi={0或1}： 






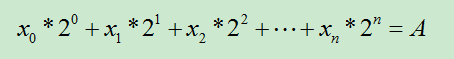
代码：




 1 # include<cstdio>
 2 # include<iostream>
 3 # include<fstream>
 4  
 5 using namespace std;
 6  
 7 # define MOD 1000000007
 8  
 9 typedef long long LL;
10  
11 struct matrix
12 {
13     LL a[2][2];
14     void init()
15     {
16         a[0][0] = 2;
17         a[0][1] = 1;
18         a[1][0] = 1;
19         a[1][1] = 0;
20     }
21 };
22  
23 int n;
24  
25 matrix fun ( matrix aa, matrix bb )
26 {
27     matrix cc;
28     for ( int i = 0;i < 2;i ++ )
29     {
30         for ( int j = 0;j < 2;j++ )
31         {
32             cc.a[i][j] = 0;
33             for ( int k = 0;k < 2;k++ )
34             {
35                 cc.a[i][j]+=(aa.a[i][k]%MOD*bb.a[k][j]%MOD)%MOD;
36             }
37             cc.a[i][j]%=MOD;
38         }
39     }
40  
41     return cc;
42 }
43  
44  
45  
46 matrix My_power( matrix aa,int k )
47 {
48     matrix  ans;
49     ans.init();
50     while ( k >= 1 )
51     {
52         if ( k&1 )
53         {
54             ans = fun(ans,aa);
55         }
56         k/=2;
57         aa = fun(aa,aa);
58     }
59  
60     return ans;
61  
62 }
63  
64  
65 int main(void)
66 {
67    // freopen("output.txt","w",stdout);
68     int n;
69  
70  
71     while ( scanf("%d",&n)!=EOF )
72     {
73         matrix aa;
74         aa.init();
75         aa = My_power(aa,n-1);
76         printf("%lld\n",aa.a[0][1]%MOD);
77     }
78  
79     return 0;
80 }
81  




 










            

            
posted @ 
2015-05-16 11:53 
BYYB_0506 
阅读(319) 
评论(0) 
编辑 
收藏 
举报