kuangbin带你飞,矩阵（简单数学推导题）

A - Jzzhu and Sequences

Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

Jzzhu has invented a kind of sequences, they meet the following property:

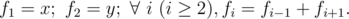
You are given x and y, please calculate f_n modulo 1000000007(10⁹ + 7).

Input

The first line contains two integers x and y(|x|, |y| ≤ 10⁹). The second line contains a single integer n(1 ≤ n ≤ 2·10⁹).

Output

Output a single integer representing f_n modulo 1000000007(10⁹ + 7).

Sample Input

Input

2 3
3

Output

1

Input

0 -1
2

Output

1000000006

Hint

In the first sample, f₂ = f₁ + f₃, 3 = 2 + f₃, f₃ = 1.

In the second sample, f₂ =  - 1;  - 1 modulo (10⁹ + 7) equals (10⁹ + 6).

 

题目大意：

　　输入f2和f1的值，最后算出fn的值。

解题思路：

f[1] = x;f[2] = y;
f[i] = f[i-1]+f[i+1]
i = 1;
f[1] = f[0]+f[2];->f[0] = x-y;
i = 2；
f[2] = f[1]+f[3];->f[3] = y-x;
i = 3;
f[3] = f[2]+f[4];->f[4] = -x;
i = 4;
f[4] = f[3]+f[5];->f[5] = -y
i = 5;
f[5] = f[4]+f[6];->f[6] = x-y;

一开始被51组数据卡了三次，原因就是在取MOD的过程中，如果a[n]<0..while ( a[n]<0 )a[n]+=MOD;将其变为正数后，才能进行a[n]%MOD的运算。

代码：

# include<cstdio>
# include<iostream>
# include<algorithm>
# include<functional>
# include<cstring>
# include<string>
# include<cstdlib>
# include<iomanip>
# include<numeric>
# include<cctype>
# include<cmath>
# include<ctime>
# include<queue>
# include<stack>
# include<list>
# include<set>
# include<map>

using namespace std;

const double PI=4.0*atan(1.0);

typedef long long LL;
typedef unsigned long long ULL;

# define inf 999999999
# define MOD 1000000007

LL a[10];
int x,y,n;
void init()
{
    a[0] = x-y;
    a[1] = x;
    a[2] = y;
    a[3] = y-x;
    a[4] = -x;
    a[5] = -y;

}

int main(void)
{
    while ( cin>>x>>y )
    {
        init();
        cin>>n;
        n%=6;
        while ( a[n]<0 )
            a[n]+=MOD;
            cout<<a[n]%MOD<<endl;
    }

    return 0;
}