数据结构+算法（搜索类：BFS + DFS ）

BFS

典型搜索树示意图

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    std::queue<Node> q; // 核心数据结构
    std::set<Node> visited; // 避免走回头路
    
    q.push(start); // 将起点加入队列
    visited.insert(start);
    int step = 0; // 记录扩散的步数

    while (!q.empty()) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            auto cur = q.front();
          	q.pop();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj()) {
                if (visited.count(x) < 0) {
                    q.push(x);
                    visited.insert(x);
                }
            }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

 

DFS

决策树

 

/*
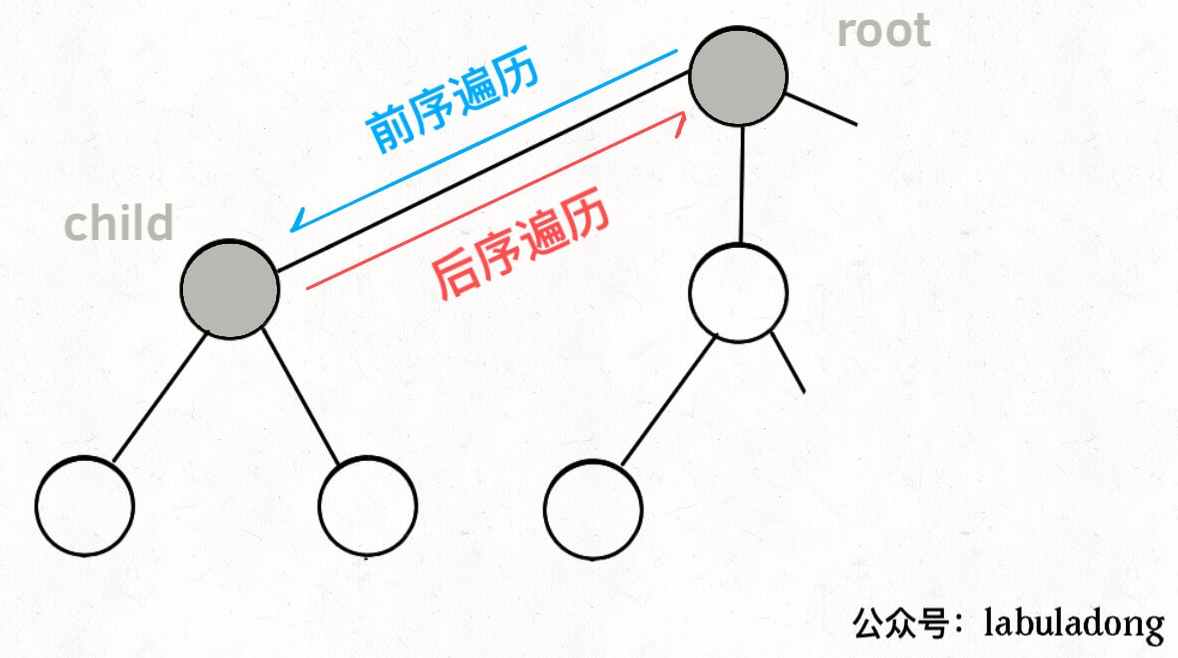
*@param: origin_source 一般是给定的输入
*@param: track_res 期望的最终结果
*@param: single_track 期望目标结果中的单个case
*@param: cur_index 当前执行的阶段
*/
void backtrack(DataType origin_source, vector<DataType> track_res, DataType& single_track，int cur_index) {
    // 触发结束条件。这里用cur_index 或者single_track 的内容做判断均可
    if (cur_index == 边界条件) { 
        track_res.push_back(single_track);
        return;
    }
    
    for (int i = 0; i < origin_source.size(); i++) {
        // 排除不合法的选择
        if (isValid())
            continue;
        // 做选择,将当前选择加入
        single_track.push(origin_source[i]);
        // 进入下一层决策树
        backtrack(origin_source, track_res, singhle_track, cur_index++);
        // 取消选择
        single_track.pop();
    }
}

岛屿类题目

void dfs(vector<vector<int>>& grid, int i, int j, vector<vector<bool>>& visited) {
    int m = grid.size(), n = grid[0].size();
    if (i < 0 || j < 0 || i >= m || j >= n) {
        return;
    }
    if (visited[i][j]) {
        return;
    }
    visited[i][j] = true;
    dfs(grid, i - 1, j, visited); // 上
    dfs(grid, i + 1, j, visited); // 下
    dfs(grid, i, j - 1, visited); // 左
    dfs(grid, i, j + 1, visited); // 右
}

上述是一般类型的模板。但是通常情况下，面对岛屿问题会选择使用“岛屿淹没法”，也就是直接将 gird[i][j] == 0 （假设0是海水),这样可以不用维护 visited 数组，同样达到了不走回头路的目的

    // 从 (i, j) 开始，将与之相邻的陆地都变成海水
    void dfs(vector<vector<char>>& grid, int i, int j) {
        int m = grid.size(), n = grid[0].size();
        if (i < 0 || j < 0 || i >= m || j >= n) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == '0') {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = '0';
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);
    }