算法笔记--FFT && NTT
推荐阅读资料:算法导论第30章
本文不做证明,详细证明请看如上资料。
FFT在算法竞赛中主要用来加速多项式的乘法
普通是多项式乘法时间复杂度的是O(n2),而用FFT求多项式的乘法可以使时间复杂度达到O(nlogn)
FFT求多项式的乘法步骤主要如下图
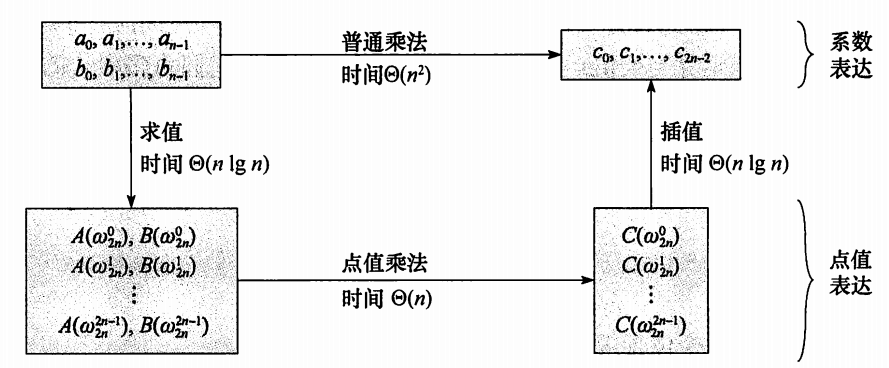
其中求值是将系数表达转换成点值表达,带入的自变量是wn=1的复数解,称为DFT
插值是将点值表达转换成系数表达,称为DFT-1
DFT 和 DFT-1都可以用FFT加速实现



这是递归版的FFT
还有一种非递归的版本
我们发现叶子节点的下表的二进制为:000 100 010 110 001 101 110 111
与它们的本身所对应的位置的二进制:000 001 010 011 100 101 011 111
相反
所以我们可以确定叶子节点的值,从下往上进行操作
求二进制反转的代码(其中L是二进制位):
for (int i = 0; i < n; i++) { R[i] = (R[i>>1]>>1) | ((i&1) << L-1); }
假设现在R[i]的二进制是abcd,没有操作之前的R[i>>1]是0abc,操作之后的是cba0,再右移是0cba,再判断原来的d是不是1在最高位放1或0,就刚好是反转的结果
模板:
递归版(以求大数乘法为例):
#include<bits/stdc++.h> using namespace std; #define fi first #define se second #define pi acos(-1.0) #define LL long long #define mp make_pair #define pb push_back #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r #define ULL unsigned LL #define pll pair<LL, LL> #define pii pair<int, int> #define piii pair<int,pii> #define mem(a, b) memset(a, b, sizeof(a)) #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); #define fopen freopen("in.txt", "r", stdin);freopen("out.txt", "w", stout); //head typedef complex<double> cd; const int N = 2e5 + 5; char a[N], b[N]; cd A[N], B[N]; int tmp[N]; void fft(cd *x, int n, int type) { if(n == 1) return ; cd l[n>>1], r[n>>1]; for (int i = 0; i < n; i += 2) { l[i>>1] = x[i]; r[i>>1] = x[i+1]; } fft(l, n>>1, type); fft(r, n>>1, type); cd wn(cos(2*pi/n), sin(type*2*pi/n)), w(1, 0), t; for(int i = 0; i < n>>1; i++, w *= wn) { t = w*r[i]; x[i] = l[i] + t; x[i+(n>>1)] = l[i] - t; } } int main() { while(~scanf("%s%s", a, b)) { int n = strlen(a), m = strlen(b); mem(A, 0); mem(B, 0); mem(tmp, 0); for (int i = n - 1; i >= 0; i--) A[n-1-i] = a[i] - '0'; for (int i = m - 1; i >= 0; i--) B[m-1-i] = b[i] - '0'; m = m + n; for(n = 1; n <= m; n <<= 1); fft(A, n, 1); fft(B, n, 1); for (int i = 0; i < n; i++) A[i] *= B[i]; fft(A, n, -1); for (int i = 0; i < m; i++) { int t = (int)(A[i].real()/n + 0.5); t += tmp[i]; tmp[i] = t%10; tmp[i+1] += t/10; } int i; for (i = m; i >= 1; i--) if(tmp[i]) break; for (i; i >= 0; i--) printf("%d", tmp[i]); printf("\n"); } return 0; }
FFT非递归版模板:
typedef complex<double> cd; const int N = 2e5 + 5; cd A[N], B[N]; int R[N]; void fft(cd *x, int n, int type) { for (int i = 0; i < n; i++) if(i < R[i]) swap(x[i], x[R[i]]); for (int i = 1; i < n; i <<= 1) { cd wn(cos(pi/i), type*sin(pi/i)); for (int j = 0; j < n; j += i<<1) { cd w(1, 0); for (int k = 0; k < i; k++, w*=wn) { cd X = x[j+k], Y = w*x[j+k+i]; x[j+k] = X+Y; x[j+k+i] = X-Y; } } } if(type == -1) { for (int i = 0; i < n; ++i) x[i]=(x[i].real()/n,x[i].imag()); } } int main() { int n, m, L = 0; scanf("%d %d", &n, &m); for (int i = 0; i < n; ++i) scanf("%d", &A[i]); for (int i = 0; i < m; ++i) scanf("%d", &B[i]); m = m + n; for(n = 1; n <= m; n <<= 1) L++; for (int i = 0; i < n; i++) R[i] = (R[i>>1]>>1) | ((i&1) << L-1); fft(A, n, 1); fft(B, n, 1); for (int i = 0; i < n; i++) A[i] *= B[i]; fft(A, n, -1); for (int i = 0; i < m; i++) printf("%d\n", (int)(A[i].real()+0.5)); return 0; }
PS:手写complex类+非递归版最快
NTT模板:
#include<bits/stdc++.h> using namespace std; /* 469762049--3 998244353--3 1004535809--3 1e9+7 -- 5 (g 是mod(r*2^k+1)的原根) 素数 r k g 3 1 1 2 5 1 2 2 17 1 4 3 97 3 5 5 193 3 6 5 257 1 8 3 7681 15 9 17 12289 3 12 11 40961 5 13 3 65537 1 16 3 786433 3 18 10 5767169 11 19 3 7340033 7 20 3 23068673 11 21 3 104857601 25 22 3 167772161 5 25 3 469762049 7 26 3 1004535809 479 21 3 2013265921 15 27 31 2281701377 17 27 3 3221225473 3 30 5 75161927681 35 31 3 77309411329 9 33 7 */ const int N = 300100, P = 998244353; inline int qpow(int x, int y) { int res(1); while (y) { if (y & 1) res = 1ll * res * x % P; x = 1ll * x * x % P; y >>= 1; } return res; } int r[N]; void ntt(int *x, int n, int opt) { register int i, j, k, m, gn, g, tmp; for (i = 0; i < n; ++i) if (r[i] < i) swap(x[i], x[r[i]]); for (m = 2; m <= n; m <<= 1) { k = m >> 1; gn = qpow(3, (P - 1) / m); ///3是原根 for (i = 0; i < n; i += m) { g = 1; for (j = 0; j < k; ++j, g = 1ll * g * gn % P) { tmp = 1ll * x[i + j + k] * g % P; x[i + j + k] = (x[i + j] - tmp + P) % P; x[i + j] = (x[i + j] + tmp) % P; } } } if (opt == -1) { reverse(x + 1, x + n); register int inv = qpow(n, P - 2); for (i = 0; i < n; ++i) x[i] = 1ll * x[i] * inv % P; } } int A[N], B[N], C[N]; int main() { int n, m, L = 0; scanf("%d %d", &n, &m); ++n, ++m; for (int i = 0; i < n; ++i) scanf("%d", &A[i]); for (int i = 0; i < m; ++i) scanf("%d", &B[i]); m = m + n; for(n = 1; n <= m; n <<= 1) L++; for (int i = 0; i < n; i++) r[i] = (r[i>>1]>>1) | ((i&1) << L-1); ntt(A, n, 1); ntt(B, n, 1); for (int i = 0; i < n; ++i) C[i] = 1ll * A[i] * B[i] % P; ntt(C, n, -1); for (int i = 0; i < m-1; ++i) printf("%d ", C[i]); puts(""); return 0; }
任意模数NTT模板:
const int maxn = 400005,maxm = 100005; int pr[]={469762049,998244353,1004535809}; int R[maxn]; inline LL qpow(LL a,LL b,LL p){ LL re = 1; a %= p; for (; b; b >>= 1,a = a * a % p) if (b & 1) re = re * a % p; return re; } struct FFT{ int G,P,A[maxn]; void NTT(int* a,int n,int f){ for (int i = 0; i < n; i++) if (i < R[i]) swap(a[i],a[R[i]]); for (int i = 1; i < n; i <<= 1){ int gn = qpow(G,(P - 1) / (i << 1),P); for (int j = 0; j < n; j += (i << 1)){ int g = 1,x,y; for (int k = 0; k < i; k++,g = 1ll * g * gn % P){ x = a[j + k],y = 1ll * g * a[j + k + i] % P; a[j + k] = (x + y) % P,a[j + k + i] = (x + P - y) % P; } } } if (f == 1) return; int nv = qpow(n,P - 2,P); reverse(a + 1,a + n); for (int i = 0; i < n; i++) a[i] = 1ll * a[i] * nv % P; } }fft[3]; int F[maxn],G[maxn],B[maxn],deg1,deg2,deg,md; LL ans[maxn]; LL inv(LL n,LL p){return qpow(n % p,p - 2,p);} LL mul(LL a,LL b,LL p){ LL re = 0; for (; b; b >>= 1,a = (a + a) % p) if (b & 1) re = (re + a) % p; return re; } void CRT(){ deg = deg1 + deg2; LL a,b,c,t,k,M = 1ll * pr[0] * pr[1]; LL inv1 = inv(pr[1],pr[0]),inv0 = inv(pr[0],pr[1]),inv3 = inv(M % pr[2],pr[2]); for (int i = 0; i <= deg; i++){ a = fft[0].A[i],b = fft[1].A[i],c = fft[2].A[i]; t = (mul(a * pr[1] % M,inv1,M) + mul(b * pr[0] % M,inv0,M)) % M; k = ((c - t % pr[2]) % pr[2] + pr[2]) % pr[2] * inv3 % pr[2]; ans[i] = ((k % md) * (M % md) % md + t % md) % md; } } void conv(){ int n = 1,L = 0; while (n <= (deg1 + deg2)) n <<= 1,L++; for (int i = 1; i < n; i++) R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1)); for (int u = 0; u <= 2; u++){ fft[u].G = 3; fft[u].P = pr[u]; for (int i = 0; i <= deg1; i++) fft[u].A[i] = F[i]; for (int i = 0; i <= deg2; i++) B[i] = G[i]; for (int i = deg2 + 1; i < n; i++) B[i] = 0; fft[u].NTT(fft[u].A,n,1); fft[u].NTT(B,n,1); for (int i = 0; i < n; i++) fft[u].A[i] = 1ll * fft[u].A[i] * B[i] % pr[u]; fft[u].NTT(fft[u].A,n,-1); } } int main(){ scanf("%d %d %d", °1, °2, &md); for (int i = 0; i <= deg1; i++) scanf("%d", &F[i]); for (int i = 0; i <= deg2; i++) scanf("%d", &G[i]); conv(); CRT(); for (int i = 0; i <= deg; i++) printf("%lld ",ans[i]); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号