算法笔记--数学之自然数幂和

1.递推求法

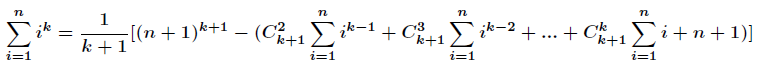
记

得到递归式：

这个可以用记忆化搜索求出S(n, k)， 复杂度：O(k * k)

例题：

ZOJ 2865

代码：

import java.util.*;
import java.math.*;

public class Main {

    /**
     * @param args
     */
    public static final int N = 100 + 10;
    public static final BigInteger f = BigInteger.ZERO.subtract(BigInteger.ONE);
    public static BigInteger C [][] = new BigInteger[N][N];
    public static BigInteger P [] = new BigInteger[N];
    public static BigInteger dp[] = new BigInteger[N];
    public static BigInteger n;
    public static int k;
    public static void init() {
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j)
                    C[i][j] = BigInteger.ZERO;
        }
        C[0][0] = BigInteger.ONE;
        for (int i = 1; i < N; ++i) {
            C[i][0] = BigInteger.ONE;
            for (int j = 1; j <= i; ++j) {
                C[i][j] = C[i-1][j-1].add(C[i-1][j]);
            }
        }
    }
    public static BigInteger DFS(int k) {
        if(dp[k].compareTo(f) != 0) return dp[k];
        if(k == 0) return dp[k] = n;
        if(k == 1) return dp[k] = n.multiply(n.add(BigInteger.ONE)).divide(BigInteger.valueOf(2));
        BigInteger res = P[k+1];
        for (int i = 2; i <= k; ++i) {
            res = res.subtract(C[k+1][i].multiply(DFS(k+1-i)));
        }
        res = res.subtract(n);
        res = res.subtract(BigInteger.ONE);
        res = res.divide(BigInteger.valueOf(k+1));
        return dp[k] = res; 
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner in = new Scanner(System.in);
        init();
        P[0] = BigInteger.ONE;
        while(in.hasNext()) {
            n = in.nextBigInteger();
            k = in.nextInt();
            for (int i = 1; i <= k+1; ++i) P[i] = P[i-1].multiply(n.add(BigInteger.ONE));
            for (int i = 0; i <= k+1; ++i) dp[i] = f;
            System.out.println(DFS(k));
        }
    }

}

2.伯努利数

伯努利数定义：

https://www.bernoulli.org/

伯努利数和自然数幂和之间的关系：

伯努利数的递推求法：

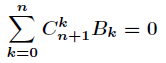
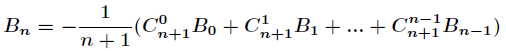
观察式子我们可以发现，可以通过O(k*k) 预处理出伯努利数，然后每次O(k)求自然数幂和

例题1：

51nod 1228

代码：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(4)
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
#define y1 y11
#define fi first
#define se second
#define pi acos(-1.0)
#define LL long long
//#define mp make_pair
#define pb push_back
#define ls rt<<1, l, m
#define rs rt<<1|1, m+1, r
#define ULL unsigned LL
#define pll pair<LL, LL>
#define pli pair<LL, int>
#define pii pair<int, int>
#define piii pair<pii, int>
#define pdd pair<double, double>
#define mem(a, b) memset(a, b, sizeof(a))
#define debug(x) cerr << #x << " = " << x << "\n";
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//head

const int N = 2e3 + 5;
const int MOD = 1e9 + 7;
LL C[N][N];
LL B[N], inv[N];
void init() {
    C[0][0] = 1;
    for (int i = 1; i < N; ++i) {
        C[i][0] = 1;
        for (int j = 1; j <= i; ++j) C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD;
    }
    inv[1] = 1;
    for (int i = 2; i < N; ++i) inv[i] = (MOD - MOD/i) * inv[MOD%i] % MOD;
    B[0] = 1;
    for (int i = 1; i < N-1; ++i) {
        LL t = 0;
        for (int j = 0; j < i; ++j) {
            t = (t + C[i+1][j]*B[j]%MOD) % MOD;
        }
        t = (-t * inv[i+1]) % MOD;
        t = (t + MOD) % MOD;
        B[i] = t;
    }
}
int main() {
    init();
    int T, k;
    LL n;
    scanf("%d", &T);
    while(T--) {
        scanf("%lld %d", &n, &k);
        LL p = 1, res = 0;
        for (int i = 1; i <= k+1; ++i) {
            p = (p * ((n+1)%MOD)) % MOD;
            res = (res + (C[k+1][i]*B[k+1-i]%MOD*p)%MOD) % MOD;
        }
        res = (res * inv[k+1]) % MOD;
        printf("%lld\n", res);
    }
    return 0;
}

 例题2：

51nod 1258

这道题k很大以至于不能O(k*k)预处理出伯努利数

于是

这种方法可以O(k*log(k))预处理伯努利数

可是不会NTT。。。未完待续

参考：

https://blog.csdn.net/ACdreamers/article/details/38929067

http://picks.logdown.com/posts/189620-the-inverse-element-of-polynomial