网络流基础

网络流基础

网络流问题

相关概念：

• 源点：有n个点，有m条有向边，有一个点很特殊，只出不进，叫做源点。
• 汇点：另一个点也很特殊，只进不出，叫做汇点。
• 容量和流量：每条有向边上有两个量，容量和流量，从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j]。
• 最大流：通俗点解释，就好比你有很多货物要从源点点运到汇点点，有向图中的一条边代表一条公路，每条公路有固定的货物装载限制（容量），对每条公路你只能运输一定数量的货物，问你每一次运输最多运到汇点点多少货物。

给定指定的一个有向图,其中有两个特殊的源点S和汇点T,每条边有指定的容量,求满足条件的从S到T的最大流。

网络流的性质

• 容量限制：f[u,v]<=c[u,v]
• 反对称性：f[u,v] = - f[v,u]
• 流量平衡：对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。

残量网络，容量网络，流量网络

残量网络=容量网络-流量网络
概念就不讲了吧，顾名思义。

增广路

增广路: 设 f 是一个容量网络 G 中的一个可行流, P 是从 Vs 到 Vt 的一条链, 若 P 满足下列条件:

• 在 P 的所有前向弧 <u, v> 上, , 即 P+ 中每一条弧都是非饱和弧;
• 在 P 的所有后向弧 <u, v> 上, , 即 P– 中每一条弧是非零流弧。

则称 P 为关于可行流 f 的一条增广路, 简称为 增广路(或称为增广链、可改进路)。沿着增广路改进可行流的操作称为增广

最小割最大流定理

割，割集

对于一张流量图G，断开一些边后，源点s和汇点t就不在连通，我们将这样的k条边的权值（即最大容量）和求和，求和后的值称为割。显然，对于一张流量图G，割有很多个且不尽相同。我们要求的就是所有割中权值最小的那一个（可能不唯一），即花最小的代价使s和t不在同一集合中。

最小割最大流定理

• 任意一个流都小于等于任意一个割
• 构造出一个流等于一个割
• 在一张流量图G中，最大流=最小割。

网络流问题解决方法

FF方法(Ford-Fulkerson)

基本思想

根据增广路定理, 为了得到最大流, 可以从任何一个可行流开始, 沿着增广路对网络流进行增广, 直到网络中不存在增广路为止,这样的算法称为增广路算法。问题的关键在于如何有效地找到增广路, 并保证算法在有限次增广后一定终止。
FF方法的基本流程是 :

• (1) 取一个可行流 f 作为初始流(如果没有给定初始流,则取零流 f= { 0 }作为初始流);
• (2) 寻找关于 f 的增广路 P,如果找到,则沿着这条增广路 P 将 f 改进成一个更大的流, 并建立相应的反向弧;
• (3) 重复第(2)步直到 f 不存在增广路为止。

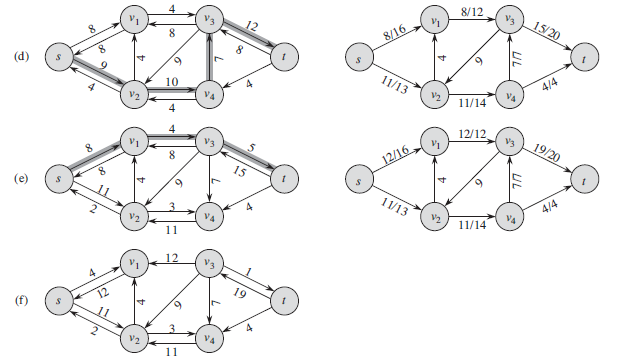
反向弧建立的意义：为程序提供反悔的机会

很明显，上图最大流应该是2，但我们找到了一条错误的路径，于是我们就应该有返回的机会，即建立反向边，这样再次从反向边流过就相当于抵消了。

算法一：EK算法（EdmondsKarp）

算法思路

在EK算法中, 程序的实现过程与增广路求最大流的过程基本一致. 即每一次更新都进行一次找增广路然后更新路径上的流量的过程。但是我们可以从上图中发现一个问题, 就是每次找到的增广路曲曲折折非常长, 此时我们往往走了冤枉路(即：明明我们可以从源点离汇点越走越近的，可是中间的几条边却向离汇点远的方向走了), 此时更新增广路的复杂度就会增加。EK 算法为了规避这个问题使用了 bfs 来寻找增广路, 然后在寻找增广路的时候总是向离汇点越来越近的方向去寻找下一个结点。

复杂度\(\varTheta(m^{2}n)\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define INF 0x7fffffff
#define N 10010
#define M 100010
using namespace std;
int n,m,ss,tt;
struct Edge{int to;int next;int value;}e[M<<1];
struct Pre{int node;int id;}pre[M<<1];//pre[i].node表示编号为i的点最短路的上一个点,pre[i].id表示最短路上连接i点的边的编号
int head[N],cnt=-1;//编号从0开始,原因见下
bool vis[N];
queue<int> q;
void add(int from,int to,int value)
{
	cnt++;
	e[cnt].to=to;
	e[cnt].value=value;
	e[cnt].next=head[from];
	head[from]=cnt;
}
bool bfs(int s,int t)//用来寻找s,t的最短路并记录,如果s,t不连通则返回0
{
	q=queue<int>();//清空队列
	memset(vis,0,sizeof(vis));
	memset(pre,-1,sizeof(pre));
	pre[s].node=s;
	vis[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=head[x];i>-1;i=e[i].next)
		{
			int now=e[i].to;
			if(!vis[now]&&e[i].value)//忽略流量为0的边
			{
				pre[now].node=x;//用pre记录最短路
				pre[now].id=i;
				vis[now]=1;
				if(now==t)return 1;//找到
				q.push(now);
			}
		}
	}
	return 0;
}

int EK(int s,int t)
{
	int ans=0;
	while(bfs(s,t))
	{
		int minv=INF;
		for(int i=t;i!=s;i=pre[i].node)
			minv=min(minv,e[pre[i].id].value);
		for(int i=t;i!=s;i=pre[i].node)
		{
			e[pre[i].id].value-=minv;
			e[pre[i].id^1].value+=minv;//x^1表示x边的反向边,此方法仅在边的编号从0开始时有效
		}
		ans+=minv;
	}
	return ans;
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d%d%d",&n,&m,&ss,&tt);
	for(int i=1;i<=m;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,0);//建立反向边
	}
	printf("%d\n",EK(ss,tt));
	return 0;
}

算法二：Dinic算法

其实Dinic算法是EK算法的改进

算法思路

发现在EK算法中，每增广一次都要先进行bfs寻找最短增广路，然而bfs后，很可能不止一条路径可以增广，如果还是按照EK算法的bfs一次增广一条路，很显然浪费了很多时间，这样，我们让bfs负责寻找增广路径，dfs计算可行的最大流。

下图1点为s点，6点为t点，红线代表寻找的路径，蓝线代表回溯的路径：

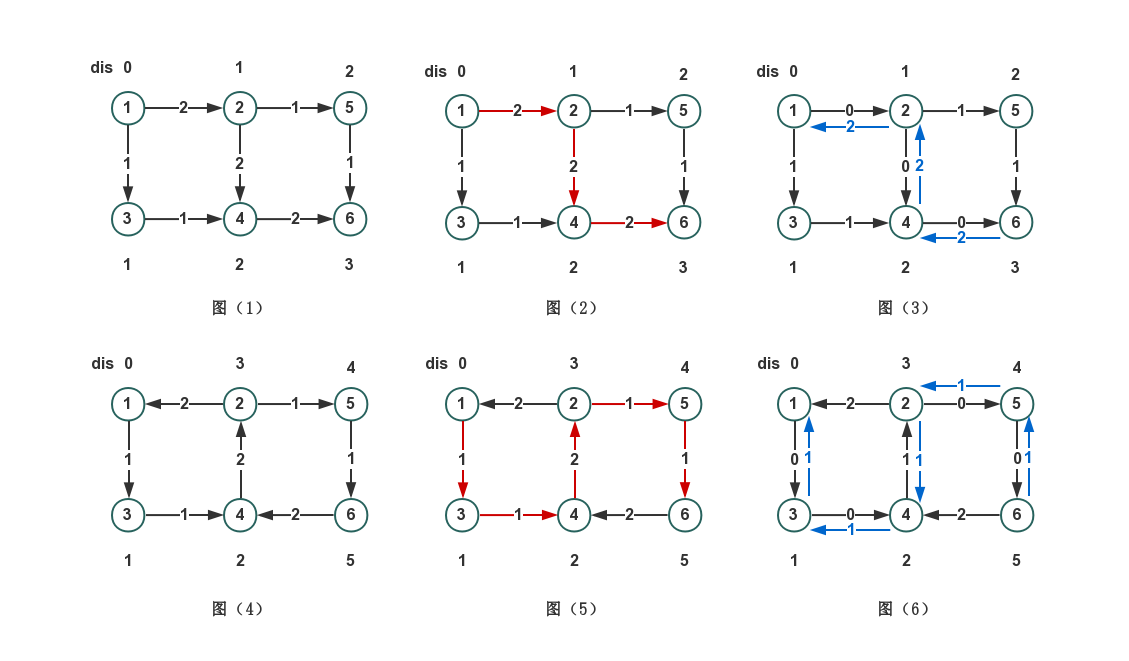
• 图1，bfs计算dis

  • 图2，dfs按最短路找到t点，累加路径上的最小容量
  • 图3，回溯，顺便更新正边和反向边的边权
  • 无其他路径，回溯到源点

• 图4，再次bfs更新dis

  • 图5，dfs按最短路找到t点，累加路径上的最小容量
  • 图6，回溯，顺便更新正边和反向边的边权
  • 无符合要求的其他路径，回溯到源点

• 再次bfs，发现s和t不连通，结束算法

复杂度：

在普通图中：\(\varTheta(n^{2}m)\)
在二分图中：\(\varTheta(m\sqrt{n})\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define N 10010
#define M 100010
#define INF 0x7fffffff
using namespace std;
int n,m,ss,tt;
int dis[N];
queue<int> q;

struct Edge{int to;int value;int next;}e[M<<1];
int head[N],cnt=-1;
void add(int from,int to,int value)
{
	cnt++;
	e[cnt].to=to;
	e[cnt].value=value;
	e[cnt].next=head[from];
	head[from]=cnt;
}

bool bfs(int s,int t)//bfs功能和EK算法的相似,不同的是Dinic中的bfs要求出所有点到源点s的最短路dis[i]
{
	q=queue<int>();//清空队列
	memset(dis,-1,sizeof(dis));
	dis[s]=0;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=head[x];i>-1;i=e[i].next)
		{
			int now=e[i].to;
			if(dis[now]==-1&&e[i].value!=0)
			{
				dis[now]=dis[x]+1;
				q.push(now);
			}
		}
	}
	return dis[t]!=-1;
}
int dfs(int x,int t,int maxflow)//表示从x出发寻找到汇点T的增广路，寻找到maxflow流量为止，并相应的增广。返回值为实际增广了多少(因为有可能找不到maxflow流量的增广路)
{
	if(x==t)return maxflow;
	int ans=0;
	for(int i=head[x];i>-1;i=e[i].next)
	{
		int now=e[i].to;
		if(dis[now]!=dis[x]+1||e[i].value==0||ans>=maxflow)continue;
		int f=dfs(now,t,min(e[i].value,maxflow-ans));
		e[i].value-=f;
		e[i^1].value+=f;
		ans+=f;
	}
	return ans;
}
int Dinic(int s,int t)
{
	int ans=0;
	while(bfs(s,t))
		ans+=dfs(s,t,INF);
	return ans;
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d%d%d",&n,&m,&ss,&tt);
	for(int i=1;i<=m;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,0);
	}
	printf("%d\n",Dinic(ss,tt));
	return 0;
}

当前弧优化

我们知道Dinic算法中的dfs是为了在可行增广路中找到最小容量并进行增广。而找增广路需要遍历每个点所连接的边，直至找到一条可到达终点的路。如果这一次找到了增广路，下一次在访问到这个点时，上一次已经检查过的边就不用再走一遍了，因为遍历一个点连接的边都是有一定顺序的，上一次访问到这个点已经确定那几条边是不可行的。于是，我们用cur[i]来表示下一次遍历边时应该从那一条开始。

虽然渐进时间复杂度没有发生变化，但实际应用中的确大大降低了Dinic的常数

优化代码(其他代码不发生变化)

int cur[N];

int dfs(int x,int t,int maxflow)
{
	if(x==t)return maxflow;
	int ans=0;
	for(int i=cur[x];i>-1;i=e[i].next)
	{
		int now=e[i].to;
		if(dis[now]!=dis[x]+1||e[i].value==0||ans>=maxflow)continue;
		cur[x]=i;//此路可行，记录此路
		int f=dfs(now,t,min(e[i].value,maxflow-ans));
		e[i].value-=f;
		e[i^1].value+=f;
		ans+=f;
	}
	return ans;
}
int Dinic(int s,int t)
{
	int ans=0;
	while(bfs(s,t))
	{
		memcpy(cur,head,sizeof(head));//初始化
		ans+=dfs(s,t,INF);
	}
	return ans;
}

网络流的优化算法还有ISAP(Improved Shortest Augumenting Path)，最高标号预流推进(HLPP)等等，Dinic在一般情况下已经够用了，其他算法自学请移步其他大佬博客喽。