最近有一个需求是已知一个变换矩阵,如何根据该矩阵获取它的位移、旋转和缩放参数?
这个问题当初书里没直接讲,但是可以通过已有的知识推导出来。
首先我们知道,图形学中的变换一般有三种:缩放、旋转和位移,它们均可以用4*4的方阵予以表达。
比如缩放矩阵的形式如下:
\(\LARGE \begin{bmatrix} sx & 0 & 0 & 0 \\ 0 & sy & 0 & 0 \\ 0 & 0 & sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
位移矩阵的形式如下:
\(\LARGE \begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
旋转矩阵则比较复杂,绕着uvw轴(两两正交且长度为1)转θ的矩阵如下:
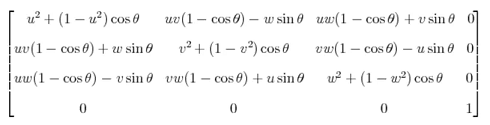
其实还有一种理解方法:在三维空间中对一个物体旋转可以理解为有一个不同于世界坐标系的坐标系,将该坐标系下的某个点转换到世界坐标系下。那么构建出的这个转换矩阵就是:
\(\LARGE \begin{bmatrix} u_x & v_x & w_x \\ u_y & v_y & w_y \\ u_z & v_z & w_z \end{bmatrix}\)
该矩阵其实就是旋转矩阵,其中u,v,w是这个坐标系的坐标轴。
我们又知道,在图形学中,可以通过矩阵相乘的方式来将各种变换操作叠加,常见的就是SRT,也就是将缩放、旋转、平移三个矩阵乘在一起组合为新矩阵,用以表达一个物体总的变换。
那么,假设我们已知一个SRT矩阵,又该如何分解出其中的S、R和T呢?
其实仔细想一下也是比较简单的,首先平移的部分始终位于矩阵的最后一列,可直接取出:

接下来,该矩阵的3*3部分是SR矩阵相乘的结果,我们又该如何进一步提取呢?
回想一下,三维旋转矩阵本身需要满足正交矩阵的性质,也就是它的每一行和每一列长度均要为1,我们可以从这一点入手,计算出该矩阵SR部分每一行的长度,它就一定是x、y、z轴的缩放!
然后再将SR部分的每一行除以sx、sy、sz就可以得到R矩阵了!


