上回说到,神经网络是由多个层的神经元组合而成,每个层的神经元接收上一层神经元节点的输出信息作为输入,然后通过sigmoid函数处理后输出到下一层,如此传递下去直到输出层,这就是前向传输算法。对于神经网络模型,我们要优化的其实就是每层之间连接的权重,这些权重可以用矩阵来予以表示。那么如何去优化权重呢,这就是我们本篇文章要介绍的后向传输算法。
在神经网络问题中,我们优化权重的目标是,使输出的值和正确的值相比误差尽可能小。设输出层第i个点计算的值为\(\LARGE o_i\),正确的值(学名叫groundtruth)为\(\LARGE t_i\),那么我们可得误差\(\LARGE e_i=(o_i - t_i)^2\),那么优化的目标可以表示为:
\(\LARGE E = min \sum \limits_{i=1} ^{n} e_i\)
如果是一个非常简单的函数,比如一些线性函数、一元二次函数等,要求它的极值是非常容易的。但是对于神经网络所组成的函数来说,这是个非常复杂的公式,是无法轻松地算出最大或最小值的,如下所示:

为了处理这种非常复杂的函数,科学家采用了一种称之为梯度下降(gradient descent)的方法来逐渐逼近最优值。它的基本思想有点类似于在黑暗的山地中行走:想象一下,在黑暗中,伸手不见五指,你知道你在一个山地中行走,你想走到坡低该怎么办呢?正常的做法是一步一个脚印地前进,当前的土地是下坡就尝试往下走,如果不是下坡就尝试往别的方向走,通过这种方式,不需要地图,也不需要事先指定的路线,就可以一步一个脚印慢慢地下山。
具体的做法参考下图,在下面的函数中,我们有一个起点,我们希望沿着向下的方向到达最小点。我们一开始选择向右走(x轴的正方向),此刻斜率为负:

假设我们向前走了一段后,到了新的位置,此时斜率为正,因此我们应该向左移动,也就是稍微减少x的值:
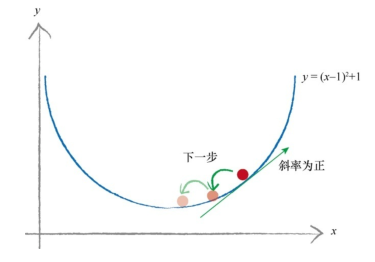
在探索的过程中,我们还需要改变步长的大小,避免在最小值的地方来回反弹,就这样走下去,斜率为负时x增加,斜率为正时x减少,一直到收敛(探索到的新的值和上一个值之间差距足够小),此时获得的值就是一个我们认为足够小的值。
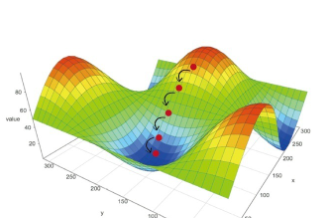
下图是一个二维函数的曲面图,可以看到这个函数有多个坡底,我们通过梯度下降所探索到的值有可能只是一个局部最小值,现实中的做法一般是我们从山上的不同点开始,多次训练神经网络,取最小的值作为最好的优化结果。
那么在实际的神经网络优化中,如何去计算E相对于每个连接权重w的斜率呢,在这里我直接给出结论:
对于三层的神经网络,输出层和隐藏层之间的斜率为:
\(\LARGE \frac{\partial E}{\partial w_{j,k}} = -(t_k - o_k) \cdot sigmoid(\sum _{i} w_{i,k}\cdot o_j)(1-sigmoid(\sum _{i} w_{i,k}\cdot o_j)) \cdot o_j\)
输入层和隐藏层之间的斜率为:
\(\LARGE \frac{\partial E}{\partial w_{i,j}} = -(e_j) \cdot sigmoid(\sum _{k} w_{k,j}\cdot o_j)(1-sigmoid(\sum _{i} w_{k,j}\cdot o_k)) \cdot o_i\)
其中\(e_j\)指的是从输出层计算的误差,经过权重分散传导到隐藏层节点j的误差值。
在计算出斜率后,我们通过如下公式更新权重:

其中α是我们选择的一个因子,这个因子可以调整变化的强度,我们通常称这个因子为学习率。
以上是基本的计算公式,可以整理成矩阵形式来加快计算速度:
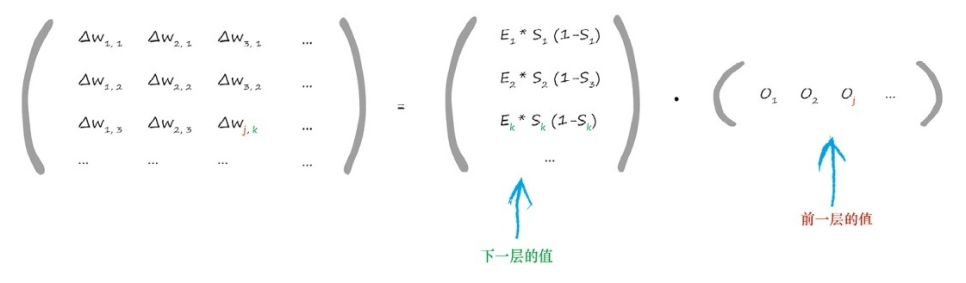
也就是:
\(\LARGE \bigtriangleup w_{j,k}=\alpha \cdot E_k \cdot o_k(1-o_k)\cdot {o_j}^T\)
其中\(o_k\)代表第k个节点的输出,其中包含了sigmoid函数。
了解了梯度下降法,接下来实现后向传播就很方便了。首先我们设定初始值,假设输入了一堆训练数据,我们可以通过前向传播计算出输出值,得到每层之间的误差,然后利用梯度下降算法计算出使输出误差最小的权重。如此一来,就通过训练得到了一个可以进行分类的神经网络。
下面我们来讲解一个实例,如下图所示,这是一个三层的神经网络,我们要更新隐藏层和输出层之间的权重w 1,1 。当前,这个值为2.0。
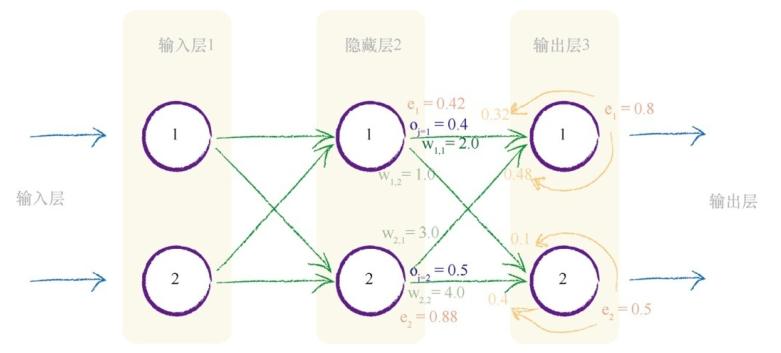
让我们重新看一下误差斜率:
\(\LARGE \frac{\partial E}{\partial w_{j,k}} = -(t_k - o_k) \cdot sigmoid(\sum _{i} w_{i,k}\cdot o_j)(1-sigmoid(\sum _{i} w_{i,k}\cdot o_j)) \cdot o_j\)
在上面的公式中,&(t_k-o_k)&的值为0.8
S函数内的求和\(\sum _{i} w_{i,k}\cdot o_j\)为2.0 * 0.4 + 3.0 * 0.5 = 2.3
sigmoid的值为0.909,那么中间的表达式为:0.909*(1-0.909)= 0.083
最后一项\(o_j=0.4\)
最后我们得到斜率 -0.8 * 0.083 * 0.4 = -0.0265
如果学习率为0.1,那么得出的改变量为-(0.1 * -0.0265)=0.00265,因此新的\(w_{1,1}=2.0+0.00265=2.00265\)
虽然这只是一个相当小的变化量,但是经过成千上百次的迭代,最终就会对所有的权重进行更新,使之与训练样本的误差最小。

