上回说到,通过一个最基本的线性方程y=ax+b,就可以构成一个简单的二维数据分类器。利用更多的直线组合,可以对数据进行更为精确的划分。那么神经网络又是如何利用这种思想进行分类的呢?我们不如先看一看生物学上神经系统的工作原理。
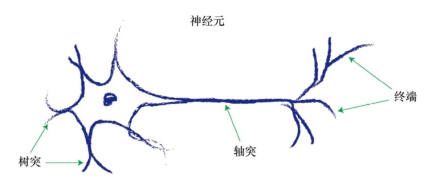
上图是一个神经元的示意图,虽然神经元有各种形式,但是所有的神经元都是将电信号从一端传输到另一端,沿着轴突将电信号从树突传到另一个树突,传到另一个神经元,最终传输到大脑等神经中枢。人体的视觉、触觉、听觉、嗅觉等感觉都是通过这种方式进行传输的。
所以我们可以对神经元的工作进行一个简化:它接受了一个电输入,输出另一个电信号到另一个神经元,输出的神经元接受了很多传输来的电信号后,再次输出给另一个神经元……以此类推。除此之外,神经元在接收到电信号后不会立刻反应,而是会抑制输入,直到输入超过了一定阈值,才会触发输出。这是有道理的——神经元不希望传递微小的噪声信号。我们常常采用S函数(又称sigmoid函数)来实现这种信号的传导转换:
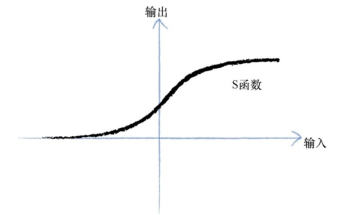
sigmoid函数具体的形式如下:
\(\LARGE y=\frac{1}{1+e^{-x}}\)
那么上面所讲的一个基本的神经元模型就如下图所示:
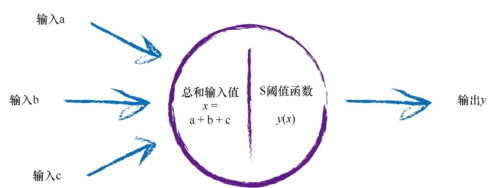
其实数学上非常简单,就是将输入信号进行累加,然后通过S函数输出信号,再传给新的神经元节点。
将这些节点叠加起来,就可以构建出多层神经元,每一层之间的节点互相连接:

对上图的模型,每一个连接之间会有一个权重,我们要调整的就是这些权重值:
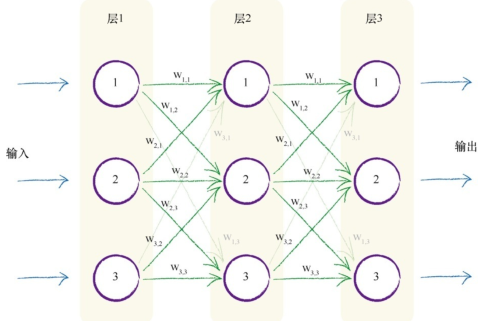
举个例子,设第n层第m个节点的值为\(d_{m,n}\),那么\(d_{2,2}=sigmoid(w_{1,2} d_{1,1} + w_{2,2} d_{1,2} + w_{3,2} d_{1,3})\),同理\(d_{2,1}\),\(d_{2,2}\),\(d_{2,3}\)也会输入到\(d_{3,2}\)中,构成最终的输出,这其实就是前向传递算法。
前向传播的计算可以利用矩阵来完成,以上图的神经网络为例,当数据从输入层到中间层时,我们可以构建一个3*3的矩阵,里面存储了权重:
\(W=
\begin{bmatrix}
w11 & w21 & w31\\
w12 & w22 & w32\\
w13 & w23 & w33\\
\end{bmatrix}
\)
设输入层输入为\(I=
\begin{bmatrix}
d11\\
d12\\
d13\\
\end{bmatrix}
\)
那么可得到第二层的数据为:
\(\LARGE D=sigmoid(WI)\)
依次也可以得到第三层的数据。因为矩阵可以很轻松地实现并行的计算,因此用矩阵来表示可以说是大大提高了计算的效率。
神经网络的基本计算方法就如上面所讲,但是想让我们的神经网络可以工作,还需要设计算法拟合出一个好的参数。这也就是我们之后要讲的后向传递算法。
