之前我们讲到BRDF定义了入射光的能量到某个方向出射光的能量之比,是一种反映物体材质的重要属性。在PBR技术中,常用的BRDF是Cook-Torrance模型,今天我们来对它进行讲解。
Cook-Torrance BRDF包含了漫反射和高光两个部分:
\(\LARGE{f_r=k_d f_{lambert} + k_s f_{cook-torrance}}\)
其中\(k_d\)和\(k_s\)分别是上文提到过的漫反射和高光的比例,\(\large{k_d + k_s = 1.0}\)。\(\large{f_{lambert}}\)是表达漫反射的brdf:
\(\LARGE{f_{lambert} = \frac{c}{\pi}}\)
其中c代表物体材质的颜色。
然而我们关注的重点还是高光的部分,\(\large{f_{cook-torrance}}\)的定义如下:
\(\LARGE{f_{cook-torrance}=\frac{DFG}{4(\omega_o \cdot n) (\omega_i \cdot n)}}\)
\(\omega_o\)和\(\omega_i\)分别指出射和入射方向,\(n\)指的是物体的normal方向,D、F、G分别指法向分布函数(normal distribution function)、菲涅尔公式(fresnel equation)和几何函数(geometry function)。下面我们将对它们三个进行讲解。
法向分布函数
法向分布函数D模拟的是微面元朝向某个向量h的比例,一般用一个概率分布函数Trowbridge-Reitz GGX来模拟:
\(\large{NDF-GGXTR(n,h,\alpha)=\frac{{\alpha}^2}{\pi {( {(n \cdot h)}^2 ({\alpha}^2 - 1) + 1)}^2}}\)
h就是half向量,即v+l;α则是粗糙度。下图展示了不同粗糙度下,同样视角和光照的对比:

当粗糙度很低的时候,只有一小片区域的微面元的朝向和h保持高度一致,因此光照聚焦于一小块地方;当粗糙度逐渐变高,则微面元朝向变得随机,则显得与h向量取向一致的微面元分布在一个大得多的半径范围内,但是同时较低的集中性也会让我们的最终效果显得更加灰暗。
几何函数
几何函数从统计学上近似的求得了微平面间相互遮蔽的比率,这种相互遮蔽会损耗光线的能量。如下图所示:
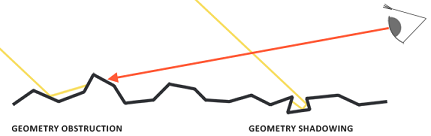
定义:
\(\large{G_{SchlickGGX}(n,v,k) = \frac{n\cdot v}{(n\cdot v)(1-k)+k}}\)
其中k是根据直接光照还是间接光照来计算的,这个之后在实现时会进一步提及,α就是前面提到的粗糙度:
\(\large{k_{direct} = \frac{{\alpha + 1}^2}{8}}\)
\(\large{k_{IBL} = \frac{{\alpha}^2}{2}}\)
最终的几何函数为:\(\large G(n,v,l,k) = G_{SchlickGGX} (n,v,k) G_{SchlickGGX} (n,l,k)\)
下图展示了不同粗糙度下所影响的几何函数的渲染效果:

可以看到,当粗糙度为0的时候,此时完全没有微面元的阴影,随着粗糙度变大,则整体也越来越暗。
第三项Fresnel的计算和定义我们下篇文章来讲。


