使用蒙特卡洛积分法的第二个问题是:如何减少求出的积分值的方差。
我们首先要知道如何去计算蒙特卡洛积分的方差,选定概率密度函数p(x)和要求积分的g(x),可计算方差为:
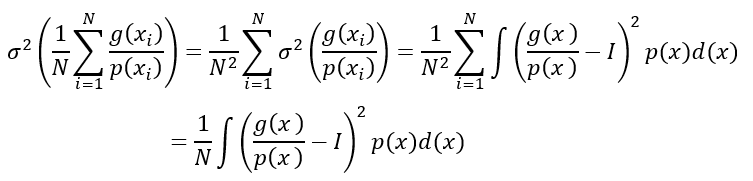
假设理想情况,σ=0,那么:
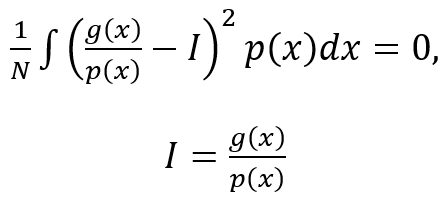
也就是p(x) = g(x)/I,此时的方差一定为0。但是I正是我们要求的积分值,所以方差为0是不可能的。
退而求其次,我们可以选择一个和g(x)函数形状较为相似的函数作为p(x)。从直观上理解,它使得每一个样本g(xi)/p(xi)趋近为常数,因为常数的方差为0,因此积分的方差也会趋近为0。
这就是所谓的重要性采样。


