Java数据结构(十三)—— 二叉排序树(BST)
二叉排序树(BST)
需求
给定数列{7,3,10,12,5,1,9},要求能够高效的完成对数据的查询和添加
思路三则
-
使用数组,缺点:插入和排序速度较慢
-
链式存储,添加较快,但查找速度慢
-
使用二叉排序树
基本介绍
对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大
图解
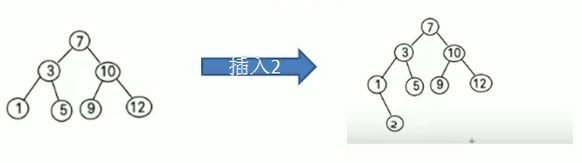
步骤
-
从数列取出第一个数成为根节点
-
取出第二个数,从根结点开始比较,大于当前节点,与右子节点比较,小于当前节点与左子节点比较
-
直到放到叶子节点
-
取出剩余的数值,重复上述步骤
建立二叉排序树
代码实现:BinarySortTree.java
package com.why.binary_sort_tree;
/**
* @Description TODO 建立二叉排序树
* @Author why
* @Date 2020/12/1 14:38
* Version 1.0
**/
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9};
BinarySortTree bst = new BinarySortTree();
for (int i = 0; i < arr.length; i++) {
Node node = new Node(arr[i]);
bst.add(node);
}
System.out.println("中序遍历二叉排序树;");
bst.midOrder();
}
}
/**
* 二叉排序树
*/
class BinarySortTree{
private Node root;
/**
* 添加节点
* @param node
*/
public void add(Node node){
if (root == null){//直接放上
root = node;
}else {
root.add(node);
}
}
/**
* 中序遍历
*/
public void midOrder(){
if (root != null){
root.midOrder();
}else {
System.out.println("二叉排序树为空");
}
}
}
/**
* 节点类
*/
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
/**
* 添加节点,递归形式,需满足二叉排序树的要求
* @param node
*/
public void add(Node node){
if (node == null){
return;
}
//判断传入的节点的值和当前子树的根节点的值的关系
if (node.value < this.value){
if (this.left == null){//当前节点左子节点为空
this.left = node;
}else {//不为空,递归向左子树添加
this.left.add(
