利用字典序法生成组合数

在组合数学的这本书中，生成组合数字有很多中方法，比较常用的序数法,字典序法
本文采用字典序法,生成一堆组合数字,即C(n,r),从n个数字中取得r个,算法完整的定义如下:

从{1,2,…,n}中取r-组合表示为C1C2…Cr，令C1＜C2＜…＜Cr，其中有i ≤Ci≤(n-r+i), i=1,2,…,r
第一个组合为{1,2 ,…，r}
生成后序组合的规则
对C1C2…Cr从右到左扫描，找出第一个满足Ci＜(n-r+i)的i
Ci<-Ci+1
Cj<-Cj-1+1 , j=i+1,i+2,…r

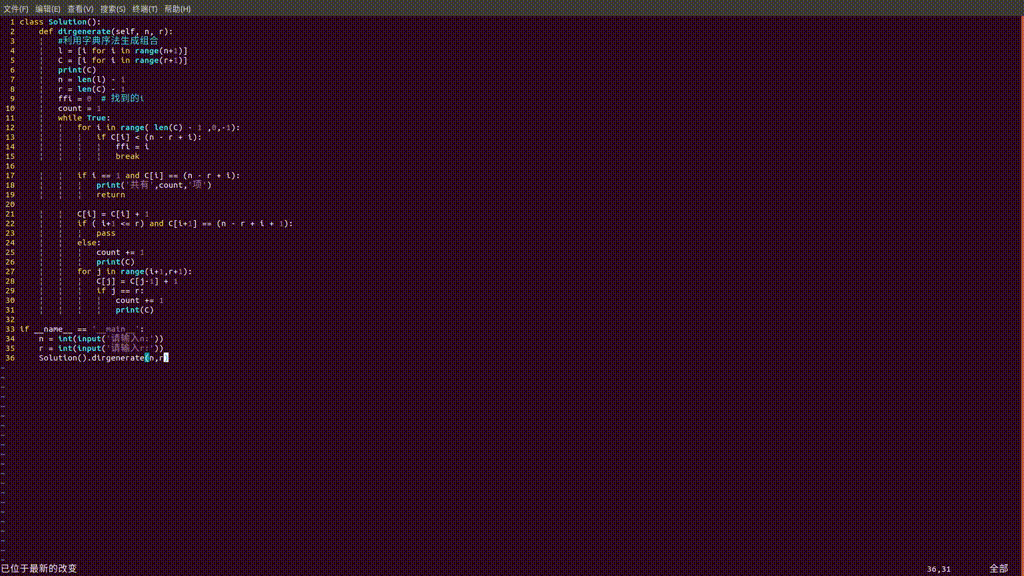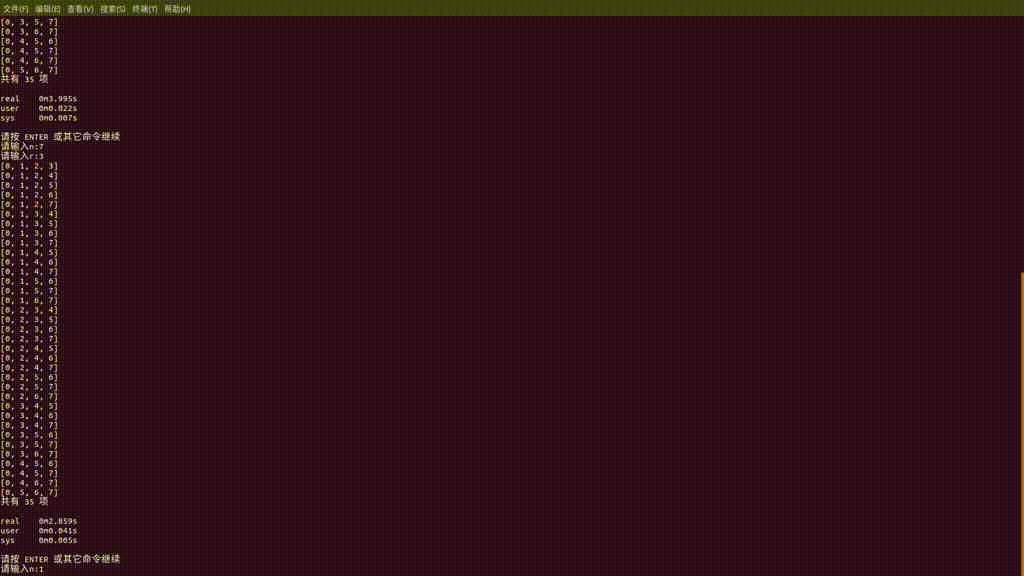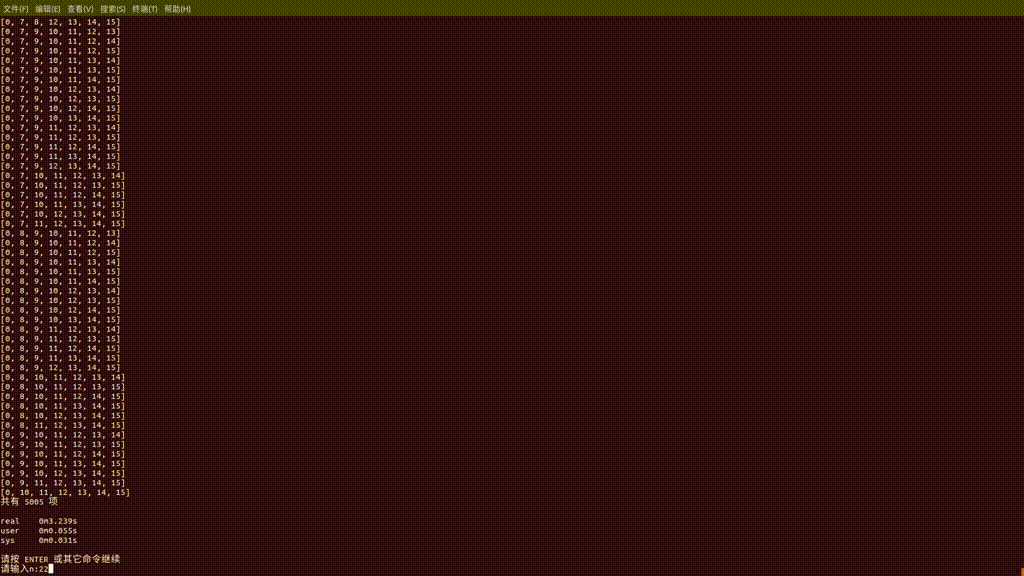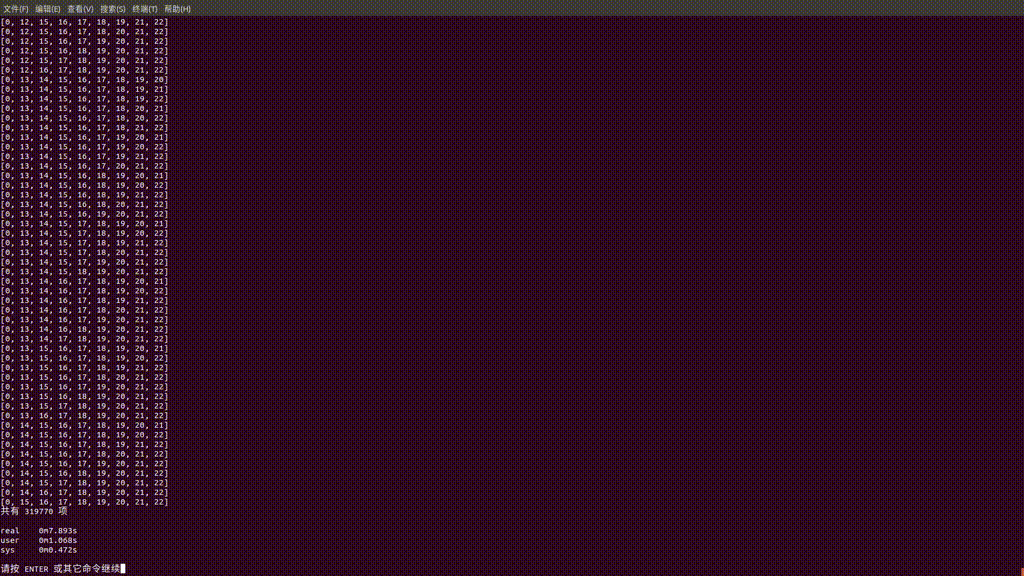
根据以上的算法描述,写出算法:

class Solution():
    def dirgenerate(self, n, r):
        #利用字典序法生成组合
        l = [i for i in range(n+1)]
        C = [i for i in range(r+1)]
        print(C)
        n = len(l) - 1
        r = len(C) - 1
        ffi = 0  # 找到的i
        count = 1
        while True:
            for i in range( len(C) - 1 ,0,-1): 
                if C[i] < (n - r + i):
                    ffi = i
                    break

            if i == 1 and C[i] == (n - r + i):  
                print('共有',count,'项')
                return

            C[i] = C[i] + 1
            if ( i+1 <= r) and C[i+1] == (n - r + i + 1):
                pass
            else:
                count += 1
                print(C)
            for j in range(i+1,r+1):
                C[j] = C[j-1] + 1
                if j == r:
                    count += 1 
                    print(C)

if __name__ == '__main__':
    n = int(input('请输入n:'))
    r = int(input('请输入r:'))
    Solution().dirgenerate(n,r)

需要注意的是:
1.算法直到产生c1=n-r+1,c2=n-r+2,...,cr=n结束,也就是说找不到ci != n-r+i 的项时结束

if i == 1 and C[i] == (n - r + i):  
        print('共有',count,'项')
        return

2.一个位数加完了之后,向前面找,并且加1,此次不输出!对之后的每一位进行加的时候也不输出

总结一下,算法的思想:就是从右向前扫,找到一个不符合Ci＜(n-r+i)的数,对其加1,如果找到的数的i,向前面进位,那么即它后面的每一项都比前一项大1

对了，最后附上算法的效果图

请输入n:8
请输入r:4
[0, 1, 2, 3, 4]
[0, 1, 2, 3, 5]
[0, 1, 2, 3, 6]
[0, 1, 2, 3, 7]
[0, 1, 2, 3, 8]
[0, 1, 2, 4, 5]
[0, 1, 2, 4, 6]
[0, 1, 2, 4, 7]
[0, 1, 2, 4, 8]
[0, 1, 2, 5, 6]
[0, 1, 2, 5, 7]
[0, 1, 2, 5, 8]
[0, 1, 2, 6, 7]
[0, 1, 2, 6, 8]
[0, 1, 2, 7, 8]
[0, 1, 3, 4, 5]
[0, 1, 3, 4, 6]
[0, 1, 3, 4, 7]
[0, 1, 3, 4, 8]
[0, 1, 3, 5, 6]
[0, 1, 3, 5, 7]
[0, 1, 3, 5, 8]
[0, 1, 3, 6, 7]
[0, 1, 3, 6, 8]
[0, 1, 3, 7, 8]
[0, 1, 4, 5, 6]
[0, 1, 4, 5, 7]
[0, 1, 4, 5, 8]
[0, 1, 4, 6, 7]
[0, 1, 4, 6, 8]
[0, 1, 4, 7, 8]
[0, 1, 5, 6, 7]
[0, 1, 5, 6, 8]
[0, 1, 5, 7, 8]
[0, 1, 6, 7, 8]
[0, 2, 3, 4, 5]
[0, 2, 3, 4, 6]
[0, 2, 3, 4, 7]
[0, 2, 3, 4, 8]
[0, 2, 3, 5, 6]
[0, 2, 3, 5, 7]
[0, 2, 3, 5, 8]
[0, 2, 3, 6, 7]
[0, 2, 3, 6, 8]
[0, 2, 3, 7, 8]
[0, 2, 4, 5, 6]
[0, 2, 4, 5, 7]
[0, 2, 4, 5, 8]
[0, 2, 4, 6, 7]
[0, 2, 4, 6, 8]
[0, 2, 4, 7, 8]
[0, 2, 5, 6, 7]
[0, 2, 5, 6, 8]
[0, 2, 5, 7, 8]
[0, 2, 6, 7, 8]
[0, 3, 4, 5, 6]
[0, 3, 4, 5, 7]
[0, 3, 4, 5, 8]
[0, 3, 4, 6, 7]
[0, 3, 4, 6, 8]
[0, 3, 4, 7, 8]
[0, 3, 5, 6, 7]
[0, 3, 5, 6, 8]
[0, 3, 5, 7, 8]
[0, 3, 6, 7, 8]
[0, 4, 5, 6, 7]
[0, 4, 5, 6, 8]
[0, 4, 5, 7, 8]
[0, 4, 6, 7, 8]
[0, 5, 6, 7, 8]
共有 70 项