神经网络与深度学习[邱锡鹏] 第四章习题解析

4-1[求探讨]

角度1：

角度2：

即：接近 0 的输入在 sigmoid 型函数上的导数较大，梯度下降速度较快

4-2

异或问题：
异或（XOR）问题可以看做是单位正方形的四个角，响应的输入模式为（0,0），（0,1），（1,1），（1,0）。第一个和第三个模式属于类0
图示为：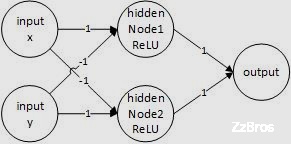
具体：

4-3

举例说明：

解决方法有[书中86-88页]：
使用带泄露的ReLU
使用带参数的ReLU
使用ELU函数
使用Softplus函数

4-4

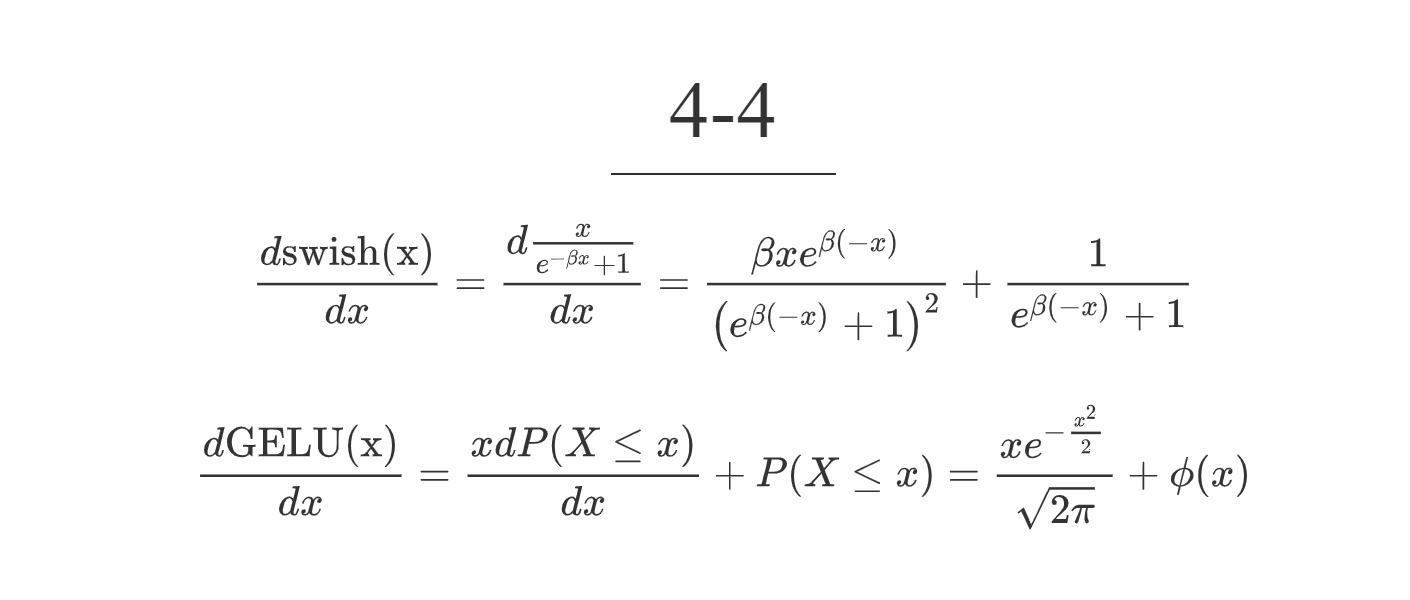
4-5

若有𝐿层隐藏层，易得用于连接输入至输出的参数矩阵共有𝐿+1层。
对于全连接网络，每一个隐藏层中的单个神经元都会与前一层的所有输出产生连接，并且每一个神经元都带有偏置,N+1个。
连接输入层与第一个隐藏层的参数量为𝑀0 × 𝑁 ÷ 𝐿
隐藏层内部连接的参数量为(𝐿-1) × 𝑁2 ÷ 𝐿2
连接𝐿层隐藏层和输出层的参数量为𝑁 ÷ 𝐿
偏置层参数量为N
参数量 M = 𝑀0 × 𝑁 ÷ 𝐿 + (𝐿-1) × 𝑁2 ÷ 𝐿2 + 𝑁 ÷ 𝐿 + N + 1

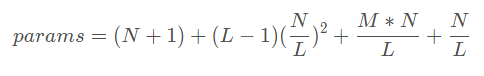
4-6[崩住了]

证明通用近似定理对于具有线性输出层和至少一个使用 ReLU 激活函数的隐藏层组成的前馈神经网络，也都是适用的．

4-7

4-8

因为如果参数都设为0，在第一遍前向计算的过程中所有的隐藏层神经元的激活值都相同。在反向传播时，所有权重更新也都相同，这样会导致隐藏层神经元没有区分性。这种现象称为对称权重现象。

4-9