Codeforces Round #633 (Div. 1)

Codeforces Round #633 (Div. 1)

A

略

B

答案最大为 \(3\)。如果用 \(2\) 种，那一定可以只用 \(1\) 种。然后看看什么情况只用 \(1\) 种（略）

C

找规律（略）

D

设选出的集合为 \(S\)，则 \(\forall u\)，以 \(u\) 为根，除了 \(u\) 的儿子外，至多在 \(u\) 的两个儿子子树中有 \(S\) 的点。证明要画个图，就粘一个吧（wucstdio）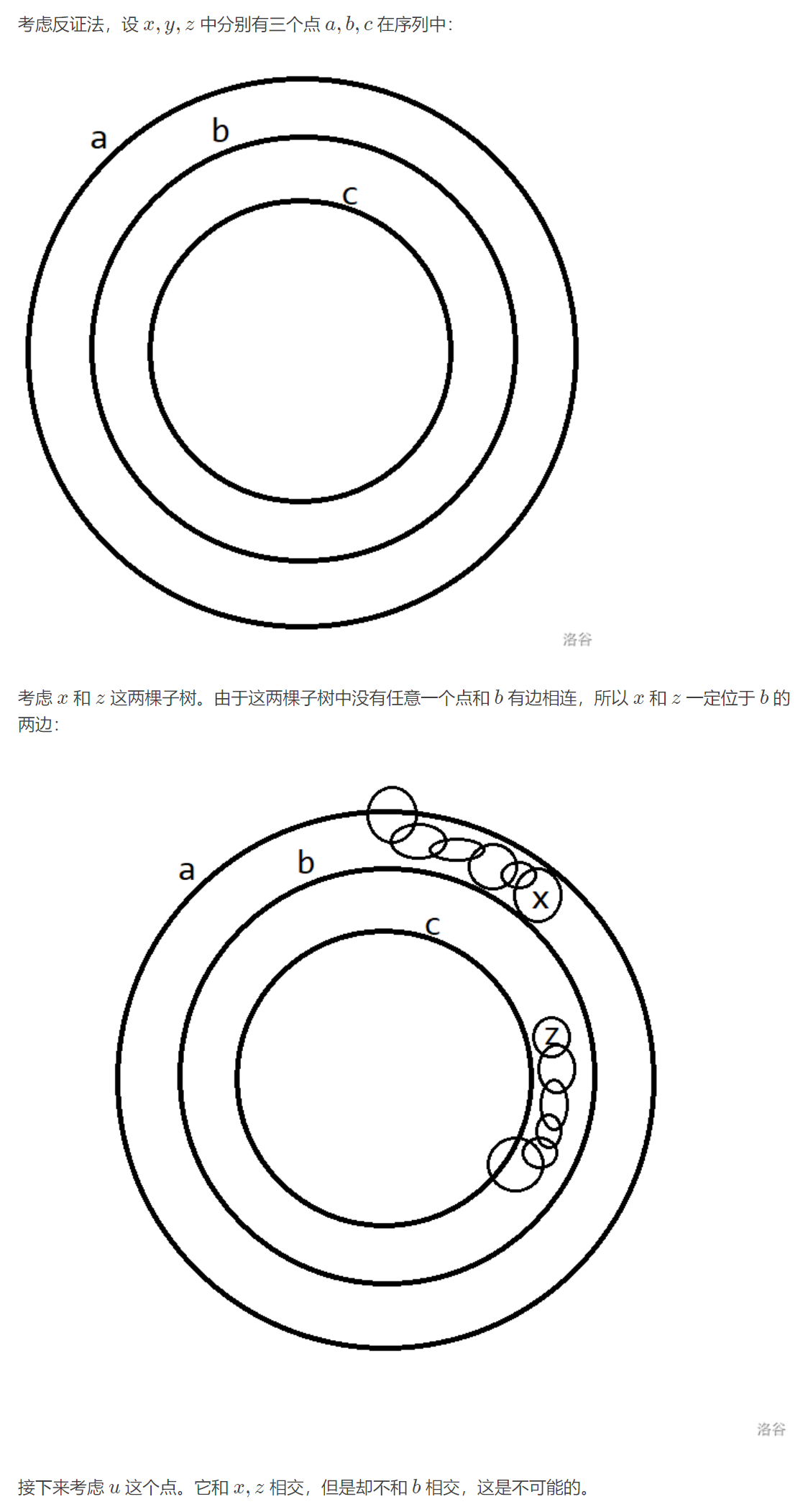

这个性质说明：可以找到一条链，\(\forall x\in S\)，\(x\) 在链上或与链相邻。然后，\(S\) 中的点显然不能相邻。根据这两个限制来搞一个树形 \(dp\) 。\(f_{i,0/1}\) 表示第 \(i\) 个点选不选的最大答案，至于转移，。。。

const int N = 1e5 + 5;
int n, res, c[N], f[N][2]; vector<int> g[N];
#define pb push_back
void add (int u, int v) {
    g[u].pb (v), g[v].pb (u), ++c[u], ++c[v];
}
void Max (int &x, const int y) { if (y > x) x = y; }
void dp (int u, int la) {
    f[u][1] = 1;
    for (int v : g[u]) if (v != la) {
        dp (v, u);
        int t = max (f[v][0], f[v][1]);
        Max (res, f[u][0] + t);
        Max (res, f[u][1] + f[v][0]);
        Max (f[u][0], t + c[u] - 2);
        Max (f[u][1], f[v][0] + 1);
    }
    Max (res, f[u][1]);
}
signed main() {
    read (n);
    for (int i = 1, u, v; i < n; ++i)
        read (u), read (v), add (u, v);
    dp (1, 0); printf ("%d\n", res);
    return 0;
}

E