SCOJ4427 / TOPOI 4404: Miss Zhao's Graph 题解

题目链接

SCOJ

TOPOI

题目描述

Problem

给定一个包含n个顶点m条边的带权有向图，找一条边数最多的路径，且路径上的边的权值严格递增。
图中可能有重边和自环。

Input Data

第一行，两个整数n和m，表示顶点数和边数。
接下来m行，每行三个整数u,v,w，表示顶点u到顶点v有一条权值为w的边。

Output Data

一行，一个整数。

Input Sample 1

3 3
1 2 1
2 3 2
3 1 3

Output Sample 1

3

 

Input Sample 2   

6 7

1 2 1

3 2 5

2 4 2

2 5 2

2 6 9

5 4 3

4 3 4

Input Sample 2

6

 

Data Limit

 

 

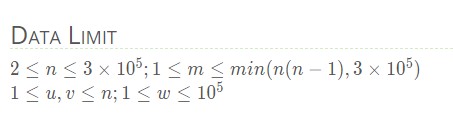
题目思路

由于我太弱了，想不出更好的做法 ，更快更强的做法请看 大佬的题解（这个可以点）

可能会有长度相同的边而又要满足严格递增是这道题中的问题所在

蒟蒻的思路很简单，用vector存以每一个节点结尾的路径信息 （数组会MLE）

信息1：这个点是由哪条边过来的  

信息2：由这条边过来的路径最大长度是多少

 

具体做法

先对每条边按长度排序，保证长度不下降

第一条边单独做，直接将信息存入vector

 

sort (a + 1, a + m + 1, cmp);  //将边按从大到小排序 
v[a[1].v].push_back((q){1, 1});  //第一条边单独处理

 

然后枚举每一条边，枚举每个u的方案，更新方案和答案

 

代码

（代码不长，但是挺慢，空间也大，大佬的强多了）

 

#include <bits/stdc++.h>
using namespace std;
const int maxn = 300008;
int n, m, ans = 1;
struct e{
	int u, v, w;
}a[maxn];  //e记录每一条边信息 
struct q{
	int num, k;   //num表示路径长度（边数），k表示由第k条边走来 
}; //q存储到每个节点方案的信息 
bool cmp (e a, e b) {
	return a.w < b.w;
}
vector <q> v[maxn];
int main(){
	scanf ("%d %d", &n, &m);
	for (int i = 1; i <= m; i++)  scanf ("%d %d %d", &a[i].u, &a[i].v, &a[i].w);
	sort (a + 1, a + m + 1, cmp);  //将边按从大到小排序 
    v[a[1].v].push_back((q){1, 1});  //第一条边单独处理 
	for (int i = 2; i <= m; i++){
		v[a[i].v].push_back((q){1, i});  //先存入vector中 
		int t = a[i].u, len = v[a[i].v].size();  //记录当前的长度（下标） 
		for (int j = 0; j < v[t].size(); j++){   //枚举u的方案 
			if (a[v[t][j].k].w < a[i].w) {      
				v[a[i].v][len-1].num = max (v[a[i].v][len-1].num, v[t][j].num + 1);
				ans = max (ans, v[a[i].v][len-1].num);
				//如果满足严格递增更新方案和答案 
			}
		}
	}
	printf ("%d", ans);
	return 0;
}