如何正确进行三/四元环计数

预处理每个点的度数 \(\deg_u\)，然后按照度数将图定向为 DAG，使得如果 \(u\to v\) 则有 \(\deg u\leq \deg v\)。

那么有性质：一个点在定向后的图中的出度不超过 \(\sqrt m\)。

证明.

假设 \(u\) 的度数 \(\deg_u\leq \sqrt m\)，于是它的出度显然不超过度数，即出度 \(\leq \sqrt m\)。

否则如果 \(u\) 的度数 \(\deg_u\geq \sqrt m\)，于是如果存在边 \(u\to v\) 则 \(v\) 的度数也 \(\geq \sqrt m\)，而总出度是 \(m\)，于是这种点的个数不超过 \(\sqrt m\)。\(\blacksquare\)

对三元环：它在定向后的图当中只有一种情况：

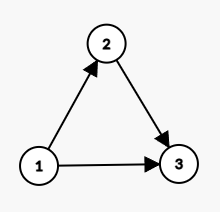
在度数最小的点上统计它的贡献：假设当前点是 \(u\)，暴力枚举 \(u\to v\) 和 \(v\to w\)，检查是否有 \(u\to w\)。

复杂度分析一下不超过 \(\sum_u \deg_u\rm{out}_u=\mathcal O(m\sqrt m)\)。

int ans = 0;
for(int i = 1; i <= n; ++i) {
    for(int v : out[i]) vis[v] = 1;
    for(int v : out[i]) for(int w : out[v]) if(vis[w]) ++ans;
    for(int v : out[i]) vis[v] = 0;
}

对四元环，在度数最大的点的对面的点上统计贡献。不难发现最后的情况是这样：

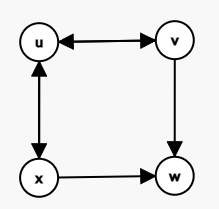
其中双向边表示不确定这条边的情况，额外要求 \(\deg_u\leq \deg_w\)。

那我们可以直接枚举所有 \(u\) 的在原图中的边 \(v\)，然后枚举 \(v\) 的出边 \(w\)，把贡献记在 \(w\) 上，最后暴力统计答案。

复杂度分析一下显然也是 \(\mathcal O(m\sqrt m)\) 的。

注意：这里不能在度数最小的点上统计答案，因为这样的话枚举顺序是先出边再原图边，而每个点的入度是没有保证的，复杂度有问题。

int ans = 0;
for(int i = 1; i <= n; ++i) {
    static int f[maxn];
    for(int v : to[i]) for(int w : out[v]) if(cmp(i, w)) ans += f[w]++;
    for(int v : to[i]) for(int w : out[v]) f[w] = 0;
}