题解 CF1338E JYPnation

题目链接

编了一个做法发现没人提出过，所以记录一下（

直接考虑图强连通的情况。发现连向一个点的所有点一定构成一条链。于是考虑求出每个点到一号点的距离。

考虑构造一棵 BFS 树。定义两个点 \(x,y\) 的小于关系，\(x<y\) 当且仅当：

• 如果 \(dis_x\neq dis_y\)，\(dis_x<dis_y\)
• 否则如果 \(fa_x\neq fa_y\)，\(fa_x<fa_y\)
• 否则存在 \(y\to x\) 的边

然后每个点的父亲为 \(dis\) 恰好等于它减一的，它连向的，所有点中的最小的点。大约是如下的一棵树：

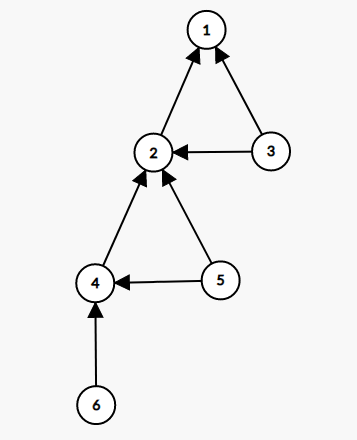
将这张图按照给出的小于关系重标号之后，有一些非常好的性质：

• 记 \(mx=fa_n\)，于是对于所有 \(i\in[2,mx-1]\)，都有 \(fa_i=1\)
• 两个点 \(j,i\)，如果 \(fa_j\leq i\) 那么存在 \(j\to i\) 的边，否则存在 \(i\to j\) 的边

一个直接的推论是这棵树的层数不会超过 \(4\)，且所有第 \(4\) 层的节点的父亲都必须是第 \(3\) 层的第一个节点。

于是不同的 \(dis\) 关系只会有 \(6\) 中，可以直接借此来讨论，复杂度 \(\mathcal O(n^2)\)。

#include<queue>
#include<cstdio>
#include<algorithm>

const int maxn = 8005;

int val[200];

int n, deg[maxn], tot, buc[maxn];
bool g[maxn][maxn], G[maxn][maxn], vis[maxn];
int dis[maxn], p[maxn], rk[maxn], fa[maxn], son[maxn];

bool chk[maxn][maxn], S[maxn][maxn];
inline bool sml(int x, int y) {
	if(x == y) return false;
	if(chk[x][y]) return S[x][y];
	
	chk[x][y] = true;
	if(dis[x] != dis[y]) return S[x][y] = dis[x] < dis[y];
	if(fa[x] != fa[y]) return S[x][y] = sml(fa[x], fa[y]);
	return S[x][y] = G[y][x];
}

std::vector<int> d[4];

int main() {
	val['0'] = 0, val['1'] = 1, val['2'] = 2, val['3'] = 3;
	val['4'] = 4, val['5'] = 5, val['6'] = 6, val['7'] = 7;
	val['8'] = 8, val['9'] = 9, val['A'] = 10, val['B'] = 11;
	val['C'] = 12, val['D'] = 13, val['E'] = 14, val['F'] = 15;
	
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) {
		getchar();
		for(int j = 1; j * 4 <= n; ++j) {
			int v = val[getchar()];
			g[i][j * 4 - 3] = v >> 3 & 1;
			g[i][j * 4 - 2] = v >> 2 & 1;
			g[i][j * 4 - 1] = v >> 1 & 1;
			g[i][j * 4 - 0] = v >> 0 & 1;
		}
	}
	
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= n; ++j)
			deg[j] += g[i][j];
	
	std::queue<int> q;
	for(int i = 1; i <= n; ++i)
		if(deg[i] == 0) q.push(i);
	
	int cnt = n; long long ans = 0;
	while(!q.empty()) {
		int u = q.front(); vis[u] = 1, q.pop();
		
		--cnt, ans += cnt * (1 + 614ll * n);
		for(int i = 1; i <= n; ++i)
			if(g[u][i] && !--deg[i]) q.push(i);
	}
	
	for(int i = 1; i <= n; ++i)
		if(!vis[i]) buc[++tot] = i;
	
	for(int i = 1; i <= tot; ++i) {
		for(int j = 1; j <= tot; ++j)
			G[i][j] = g[buc[i]][buc[j]];
		G[i][i] = 1;
	}
	n = tot;
	
	std::fill(dis, dis + n + 1, 1E+9);
	
	q.push(1), dis[1] = 0;
	while(!q.empty()) {
		int u = q.front(); q.pop();
		for(int i = 1; i <= n; ++i)
			if(G[i][u] && dis[i] > dis[u] + 1)
				dis[i] = dis[u] + 1, q.push(i);
	}
	
	for(int i = 1; i <= n; ++i) d[dis[i]].push_back(i);
	for(int i = 1; i <= 3; ++i)
		for(int x : d[i]) {
			for(int y : d[i - 1])
				if(G[x][y] && (!fa[x] || sml(y, fa[x]))) fa[x] = y;
			++son[fa[x]];
		}
	
	for(int i = 1; i <= n; ++i) p[i] = i;
	std::sort(p + 1, p + n + 1, sml);
	for(int i = 1; i <= n; ++i) rk[p[i]] = i;
	
	for(int i = 1; i <= n; ++i) son[p[i]] += son[p[i - 1]];
	
	for(int i = 2; i <= n; ++i)
		ans += dis[i] + 1 + (dis[i] == 1) + (son[i] == son[1]);
	
	for(int i = 2; i <= n; ++i) {
		for(int j = i + 1; j <= n; ++j) {
			int x = i, y = j;
			
			if(!sml(x, y)) std::swap(x, y);
			if(dis[x] == 1 && dis[y] == 1) ans += 3 + (son[y] == son[x]);
			if(dis[x] == 1 && dis[y] == 2) ans += 3;
			if(dis[x] == 2 && dis[y] == 2) ans += 3 + (fa[x] == fa[y]);
			if(dis[x] == 1 && dis[y] == 3) ans += 3 + sml(x, fa[fa[y]]);
			if(dis[x] == 2 && dis[y] == 3) ans += 3 + sml(x, fa[y]);
			if(dis[x] == 3 && dis[y] == 3) ans += 4;
		}
	}
	
	printf("%lld\n", ans);
}