平衡树
二叉搜索树是这样的一棵二叉树:每个节点的左子树中的所有节点的值都小于当前节点的值,每个节点的右子树中的所有节点的值都大于当前节点的值。平均情况下,树高是 \(O(\log n)\),所以我们可以 \(O(\log n)\) 地找出一个值对应的节点或者插入、删除一个值。但是有时候会有一些极限数据使得树退化成链,以至于所有操作都退化成 \(O(n)\)。所以我们需要保证树高,这就产生了二叉平衡树。
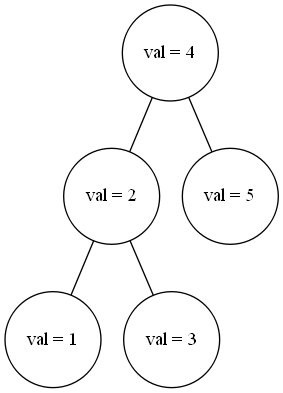
二叉平衡树有很多种,如 Treap,Splay,替罪羊树,红黑树。算法竞赛中最常用的就是 Splay 和无旋 Treap(又称FHQ Treap,由范浩强大佬发明)。
Treap(树堆)由两部分组成,即 Treap = Tree + Heap。对于每个节点,我们给其赋一个随机权值,并在原值满足二叉搜索树性质的同时要求所有附加权值满足堆(大根堆或小根堆)性质。
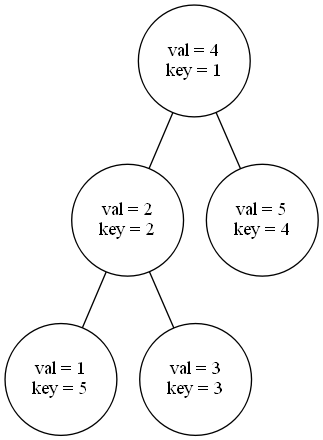
Treap 分为带旋和无旋的两种,这里仅介绍无旋的那种。对于一棵无旋 Treap,最重要的操作是分裂 split 和合并 merge。merge 操作传入两棵 Treap 的根 u 和 v,返回它们合并后的根节点。同时要求 u 中的每个节点的 val 均小于 v 中的每个节点的 val,所以只需要比较 key,这个可以通过递归来实现。
int Merge(int u, int v) {
if(!u || !v) return u ^ v;
if(t[u].key < t[v].key) {
t[u].ch[1] = Merge(t[u].ch[1], v);
return Update(u), u;
} else {
t[v].ch[0] = Merge(u, t[v].ch[0]);
return Update(v), v;
}
}
而 split 操作,传入一个根节点 u,一个值 val,和两个引用 l,r。表示将 u 为根的 Treap 分裂按照小于等于 val 和大于 val 分裂后较小者为 l,较大者为 r。这个也可以用递归实现。
void Split(int u, int val, int &l, int &r) {
if(!u) return l = r = 0, void();
if(t[u].val <= val) l = u, Split(t[u].ch[1], val, t[u].ch[1], r);
else r = u, Split(t[u].ch[0], val, l, t[u].ch[0]);
Update(u);
}
其他操作均较为简单,不再赘述。
#include<cstdio>
#include<algorithm>
#include<ctime>
const int maxn = 1E+5 + 5;
int n, op, x, root, cnt;
struct nrTreapNode {
int val, key;
int siz, cnt;
int ch[2], fa;
} t[maxn];
inline void Update(int u) {
t[u].siz = t[t[u].ch[0]].siz + t[t[u].ch[1]].siz + t[u].cnt;
t[t[u].ch[0]].fa = t[t[u].ch[1]].fa = u;
}
int Merge(int u, int v) {
if(!u || !v) return u ^ v;
if(t[u].key < t[v].key) {
t[u].ch[1] = Merge(t[u].ch[1], v);
return Update(u), u;
} else {
t[v].ch[0] = Merge(u, t[v].ch[0]);
return Update(v), v;
}
}
void Split(int u, int val, int &l, int &r) {
if(!u) return l = r = 0, void();
if(t[u].val <= val) l = u, Split(t[u].ch[1], val, t[u].ch[1], r);
else r = u, Split(t[u].ch[0], val, l, t[u].ch[0]);
Update(u);
}
int Find(int val) {
int now = root;
while(now) {
if(t[now].val == val) return now;
else if(val < t[now].val) now = t[now].ch[0];
else now = t[now].ch[1];
}
return 0;
}
void Insert(int val) {
int pos = Find(val), l, r;
if(pos) {
++t[pos].cnt;
while(pos) Update(pos), pos = t[pos].fa;
return;
}
t[++cnt] = { val, rand(), 1, 1, { 0, 0 }, 0 };
Split(root, val, l, r), l = Merge(l, cnt), root = Merge(l, r);
}
void Erase(int val) { //删除节点时,为方便起见,不删去节点,只修改 cnt 和 siz。
int pos = Find(val);
if(pos) {
if(t[pos].cnt) --t[pos].cnt;
while(pos) Update(pos), pos = t[pos].fa;
}
}
int GetRank(int val, bool op) {
int now = root, res = 0;
while(now) {
if(t[now].val == val) return res + t[t[now].ch[0]].siz + (!op ? 1 : t[now].cnt);
else if(val < t[now].val) now = t[now].ch[0];
else res += t[t[now].ch[0]].siz + t[now].cnt, now = t[now].ch[1];
}
return !op ? res + 1 : res;
}
int Rank(int k) {
int now = root;
while(now) {
if(k > t[t[now].ch[0]].siz + t[now].cnt)
k -= t[t[now].ch[0]].siz + t[now].cnt, now = t[now].ch[1];
else if(k > t[t[now].ch[0]].siz) return t[now].val;
else now = t[now].ch[0];
}
return -1;
}
inline int GetPre(int val) { return Rank(GetRank(val, 0) - 1); }
inline int GetNxt(int val) { return Rank(GetRank(val, 1) + 1); }
int main() {
srand((unsigned int)time(NULL));
scanf("%d", &n);
while(n --> 0) {
scanf("%d%d", &op, &x);
if(op == 1) Insert(x);
if(op == 2) Erase(x);
if(op == 3) printf("%d\n", GetRank(x, 0));
if(op == 4) printf("%d\n", Rank(x));
if(op == 5) printf("%d\n", GetPre(x));
if(op == 6) printf("%d\n", GetNxt(x));
}
}
而 Splay 是最能体现旋转操作作用的一种平衡树。旋转分为左旋和右旋,它们满足旋转前后树的中序遍历不变,也即不改变二叉搜索树的性质。有这样一张著名的图:

具体实现也很简单:
void Rotate(int u) {
bool Whi = Which(u), WhiFa = Which(s[u].fa);
int fa = s[u].fa, grand = s[fa].fa, son = s[u].ch[Whi ^ 1];
PushDown(fa), PushDown(u);
if(grand) s[grand].ch[WhiFa] = u;
s[u].fa = grand;
s[fa].fa = u, s[u].ch[Whi ^ 1] = fa;
s[fa].ch[Whi] = son, s[son].fa = fa;
PushUp(fa), PushUp(u);
}
然后就是最著名的 Splay(伸展)操作,它通过不断旋转,将一个节点旋转到目标节点的儿子处。而在旋转过程中,如果父亲和自己在同一条直线上,则先旋转父亲再旋转自己,否则旋转两次自己,这是为了使二叉搜索树的形态尽可能平均,而不至于退化。
void Splay(int u, int goal) {
while(s[u].fa != goal) {
int fa = s[u].fa, grand = s[fa].fa;
if(grand != goal)
Rotate(Which(u) ^ Which(fa) ? u : fa);
Rotate(u);
}
if(!goal) root = u;
}
其他操作就十分简单了。
Splay 支持一系列区间上的操作,最著名的就是区间翻转,它通过按照数组中的下标建立平衡树,每次需要翻转的时候就把左端点前一个旋转到根,再把右端点后一个旋转到它的右儿子,从而保证了整个需要翻转的区间都变成了一颗子树,从而在根处打标记来实现翻转区间。
#include<algorithm>
#include<cstdio>
const int maxn = 1E+5 + 5;
const int INF = 0x3f3f3f3f;
int n, m, cnt, root;
int a[maxn];
struct SplayNode {
int val, tag, siz, cnt;
int fa, ch[2];
} s[maxn];
inline bool Which(int u) { return s[s[u].fa].ch[1] == u; }
inline void PushUp(int u) { s[u].siz = s[s[u].ch[0]].siz + s[s[u].ch[1]].siz + s[u].cnt; }
inline void PushDown(int u) {
if(s[u].tag) {
s[s[u].ch[0]].tag ^= 1, s[s[u].ch[1]].tag ^= 1;
std::swap(s[u].ch[0], s[u].ch[1]), s[u].tag = 0;
}
}
int Build(int l, int r, int fa) {
if(l > r) return 0;
int mid = l + r >> 1, u = ++cnt;
s[u].val = a[mid], s[u].fa = fa, s[u].cnt = 1;
s[u].ch[0] = Build(l, mid - 1, u);
s[u].ch[1] = Build(mid + 1, r, u);
return PushUp(u), u;
}
void Rotate(int u) {
bool Whi = Which(u), WhiFa = Which(s[u].fa);
int fa = s[u].fa, grand = s[fa].fa, son = s[u].ch[Whi ^ 1];
PushDown(fa), PushDown(u);
if(grand) s[grand].ch[WhiFa] = u;
s[u].fa = grand;
s[fa].fa = u, s[u].ch[Whi ^ 1] = fa;
s[fa].ch[Whi] = son, s[son].fa = fa;
PushUp(fa), PushUp(u);
}
void Splay(int u, int goal) {
while(s[u].fa != goal) {
int fa = s[u].fa, grand = s[fa].fa;
if(grand != goal)
Rotate(Which(u) ^ Which(fa) ? u : fa);
Rotate(u);
}
if(!goal) root = u;
}
int RankPos(int k) {
int pos = root;
while(pos) {
PushDown(pos);
if(k > s[s[pos].ch[0]].siz + s[pos].cnt)
k -= s[s[pos].ch[0]].siz + s[pos].cnt, pos = s[pos].ch[1];
else if(k > s[s[pos].ch[0]].siz) return pos;
else pos = s[pos].ch[0];
}
return -1;
}
void Reverse(int l, int r) {
l = RankPos(l), r = RankPos(r);
Splay(l, 0), Splay(r, l);
s[s[r].ch[0]].tag ^= 1;
}
void DFS(int u) {
PushDown(u);
if(s[u].ch[0]) DFS(s[u].ch[0]);
if(s[u].val != INF && s[u].val != -INF) printf("%d ", s[u].val);
if(s[u].ch[1]) DFS(s[u].ch[1]);
}
int main() {
scanf("%d%d", &n, &m);
a[1] = -INF, a[n + 2] = INF;
for(int i = 2; i <= n + 1; ++i) a[i] = i - 1;
root = Build(1, n + 2, 0);
while(m --> 0) {
int l, r;
scanf("%d%d", &l, &r);
Reverse(l, r + 2);
}
DFS(root);
}


