题解 LA2756

题目大意 \(n\) 组数据，每组数据给定一个整数 \(m\)。求出最少的交换次数，使得围成一圈的 \(m\) 个人的左右两人交换（比如 1->2->3->1 变成 3->2->1->3），且每次只交换相邻的两个人。

分析 我们先来证明一个引理。

引理 将圆圈翻转的最优过程一定可以被划分为两个部分，使得两序列中各自被翻转。

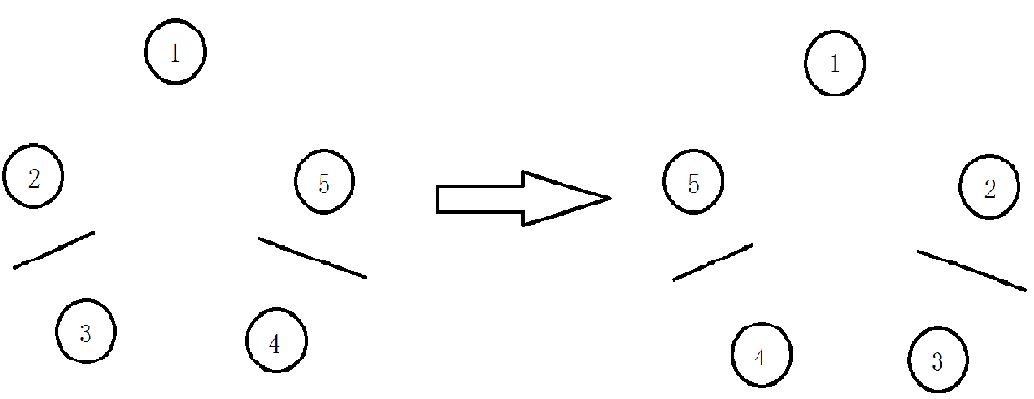
证明 \(m=1\) 时显然成立。假定对 \(m\) 成立，考虑 \(m+1\) 的情况。由于对于 \(m\) 成立，所以考虑第 \(m+1\) 个点不动。此时其它 \(m\) 个点已排好，而 \(m+1\) 需要绕到对面去，这就说明它要么与左边的在一起构成一个翻转序列，要么和右面的一起。假如第 \(m+1\) 个点动了，这不会影响其余点的顺序。由于最优，则该点要么一直往左走到对面，要么一直往右走到对面，等价于与左边或右边构成一个翻转序列。由数学归纳法，原命题成立。

而对于一个长度为 \(L\) 的翻转序列，其交换次数为 \(\frac{L(L-1)}{2}\)，所以简单计算可得，将圆圈尽量划分为长度相等的两部分是最优的。

#include<bits/stdc++.h>
using namespace std;

int n, x;

int f(int x)
{
	return x * (x - 1) / 2;
}

int main()
{
	scanf("%d", &n);
	while(n--) {
		scanf("%d", &x);
		printf("%d\n", f(x / 2) + f((x + 1) / 2));
	}
}