NE555构成多谐振荡器及三角波、正弦波的生成
NE555通过外接\(R1、R2、C\)可输出占空比、频率可调的方波，再通过积分电路对NE555输出的方波进行积分来实现三角波的输出，再通过低通滤波器对三角波进行滤波便可得到正弦波。
使用multism生成占空比为50%,频率为1kHZ,低电位为\(0V\),高电位为\(5V\)多谐振荡发生器。
积分产生三角波
积分电路的 公式为：\(V_{out}=-\frac{1}{RC}\int{V_{in}*dt}\)
通过调节\(RC\)的值可以调节三角波的幅值。
对矩形波高电位积分：
\(V_{out_H}=-\frac{1}{1000*0.0000001}*{5*0.0005}=-2.5V\)
对矩形波高电位积分：
\(V_{out_L}=-\frac{1}{1000*0.0000001}*{0*0.0005}=0V\)
我们会发现对低电位(0V)的积分抵消不了高电位(5V)的积分
会造成我们无法正常输出三角波，所以我们要抬高积分电路的参考电位点(同相端的电位)。
当输入积分电路的矩形波为\(\pm5V\)时，参考电位点为\(0V\)时，便可通过积分得到三角波，因为
对矩形波高电位积分：
\(V_{out_H}=-\frac{1}{1000*0.0000001}*{5*0.0005}=-2.5V\)
对矩形波高电位积分：
\(V_{out_L}=-\frac{1}{1000*0.0000001}*{-5*0.0005}=2.5V\)
可以相互抵消，使其在一个周期后内起点为0电位点，终点也为0电位点。
所以我们对同相端的电位进行调整，使其满足
\(V_{out_H}+V_{out_L}=0\)
\(-\frac{1}{1000*0.0000001}*{(5-V_{+})*0.0005}=\frac{1}{1000*0.0000001}*{(V_{+}-0)*0.0005}\)
\(V_+\)为同相端电位
这里我们通过可变电阻调节\(V_+\)，通过调节\(V_+\)直到满足上述条件时，便可输出三角波。
低通滤波产生正弦波
一阶无源低通滤波参考：限幅与滞后滤波算法
积分输出的三角波频率为1khz,对其做傅里叶分解，
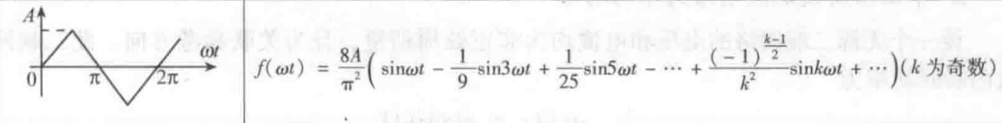
发现其基波为1khz的正弦波，通过低通滤波器来滤除(抑制)大于1khz的谐波信号，便可以得到正弦波。
低通滤波的截止频率为：\(\frac{1}{2πRC}\)
通过波特测试仪可以看出低通滤波的频率响应，截止频率大概在1khz左右。
波形输出正常。
二阶带通滤波滤出3次谐波
简单二阶带通滤波器电路如图所示，其中R1、C1 构成了低通滤波器，C2、R3 构成了高 通滤波器。
(1) 传递函数
(2) 频率特性
我们只需要给出\(A_{up}、B(带宽)、f_0(中心频率)\)，就可以计算出电路中\(R_1、R_2、R_3\)的值。
中心频率为3khz左右。
可以滤出三次谐波，滤出频率为3khz左右。
整体显示
*multism文件下载地址*
