MPU6050加速度、角速度的解算以及互补滤波使用
MPU6050加速度的解算


先根据两张图建立各个角度的关系
| \(Roll\)(横滚角) | 以\(x\)轴为旋转轴的旋转角度 |
|---|---|
| \(Yaw\)(偏航角) | 以\(z\)轴为旋转轴的旋转角度 |
| \(Pitch\)(俯仰角) | 以\(y\)轴为旋转轴的旋转角度 |
| 我们先了解加速度的单位及量程方便进行解算 | |
| 在MPU初始化函数中找到初始化加速度传感器的函数 |
//设置MPU6050加速度传感器满量程范围
//fsr:0,±2g;1,±4g;2,±8g;3,±16g
//返回值:0,设置成功
// 其他,设置失败
u8 MPU_Set_Accel_Fsr(u8 fsr)
{
return MPU_Write_Byte(MPU_ACCEL_CFG_REG,fsr<<3);//设置加速度传感器满量程范围
}
通过寄存器找到数据手册中的说明

比如我们设置量程为\(\pm2g\)
mpu是通过ADC采集电压的值来输出加速度值,
而数据寄存器是16位且最高一位为符号位,
即ADC读取的值位\(\pm32768\),对应\(\pm2g\),
\(1g\)对应的ADC值为\(+32768/2\),即16384\(LSB/g\)为数据分辨率
同样可得\(\pm4g\),数据分辨率为\(+32768/4=8192LSB/g\)
通过上面的说明我们可以把mpu读取到的原始数据解算为加速度
即:\(Gx=aacx/16384\)单位为\(m/s^2\)
我们选择\(Pitch\)解算
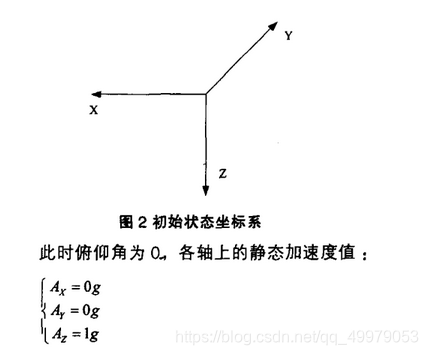
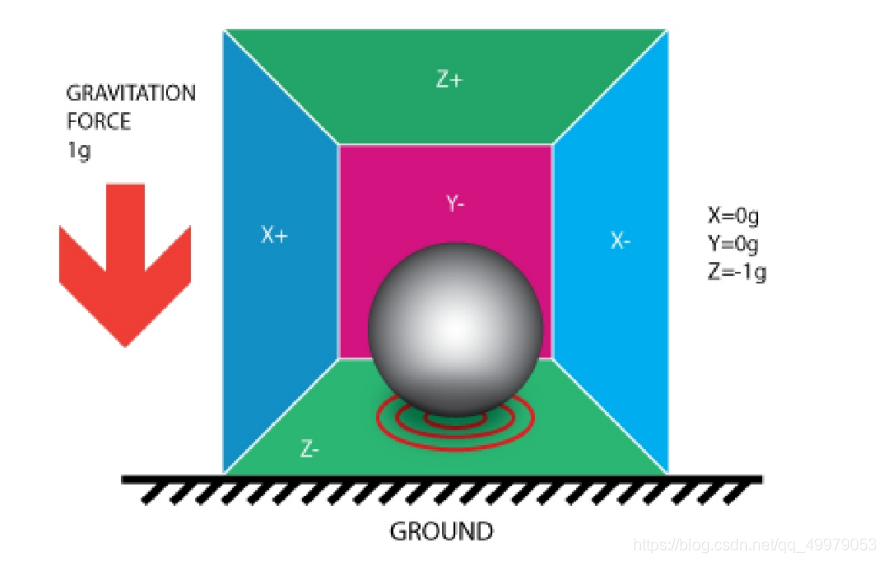
水平状态时只有\(z\)轴有加速度且加速度为\(1g\)
绕\(y\)轴旋转后:
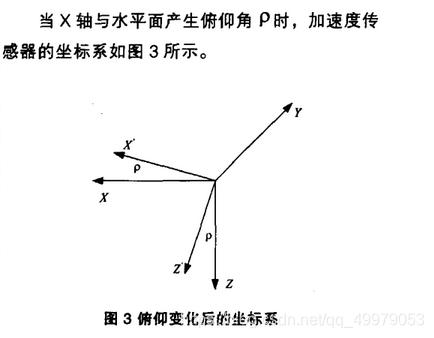
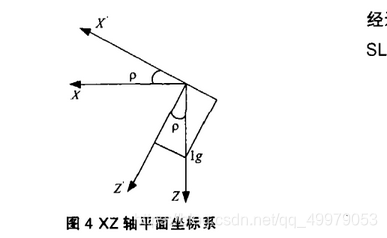
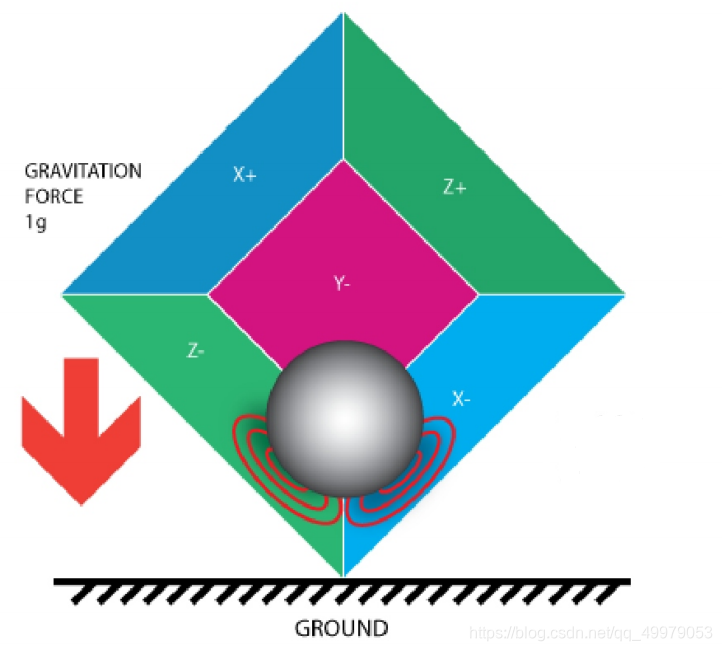
\(x^、\)为绕\(y\)轴旋转后的\(z\)轴加速度方向
\(z^、\)为绕\(y\)轴旋转后的\(z\)轴加速度方向
由图\((4)\)可得\(\rho=arctan\frac{Gx}{Gz}\),
\(\frac{Gx}{Gz}=\frac{aacx}{aacz}\)(分辨率计算后抵消)
\(\rho\)的结果为弧度制,我们将其转化为角度制
\(Pitch=\frac{\rho*2π}{360}\),
最终的公式为:
\(Pitch=arctan\frac{aacx}{aacz}*\frac{2π}{360}\),
\(\frac{2π}{360}=57.2974\)
\(Pitch=arctan\frac{aacx}{aacz}*57.2974\),
代码如下:
mpu_dmp_get_data(&pitch,&roll,&yaw); //得到姿态角即欧拉角
MPU_Get_Accelerometer(&aacx,&aacy,&aacz); //得到加速度传感器数据
MPU_Get_Gyroscope(&gyrox,&gyroy,&gyroz); //得到陀螺仪数据
Acc_Pitch=atan((float)aacx/(float)aacz)*57.2974;
printf("%f %f\r\n",pitch,Acc_Pitch);
我们与DMP处理后的\(Pitch\)进行比较
数据相差一个负号
将公式变为: \(Pitch=-arctan\frac{aacx}{aacz}*57.2974\)即可
代码也对应的进行修改:
mpu_dmp_get_data(&pitch,&roll,&yaw); //得到姿态角即欧拉角
MPU_Get_Accelerometer(&aacx,&aacy,&aacz); //得到加速度传感器数据
MPU_Get_Gyroscope(&gyrox,&gyroy,&gyroz); //得到陀螺仪数据
Acc_Pitch=-atan((float)aacx/(float)aacz)*57.2974;
printf("%f %f\r\n",pitch,Acc_Pitch);
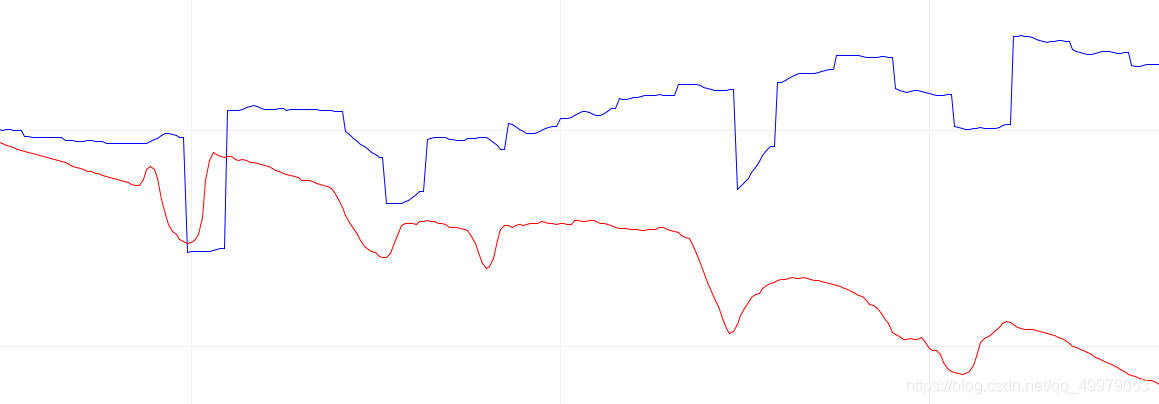
输出数据波形:
红色为加速度解算
蓝色为\(DMP\)解算
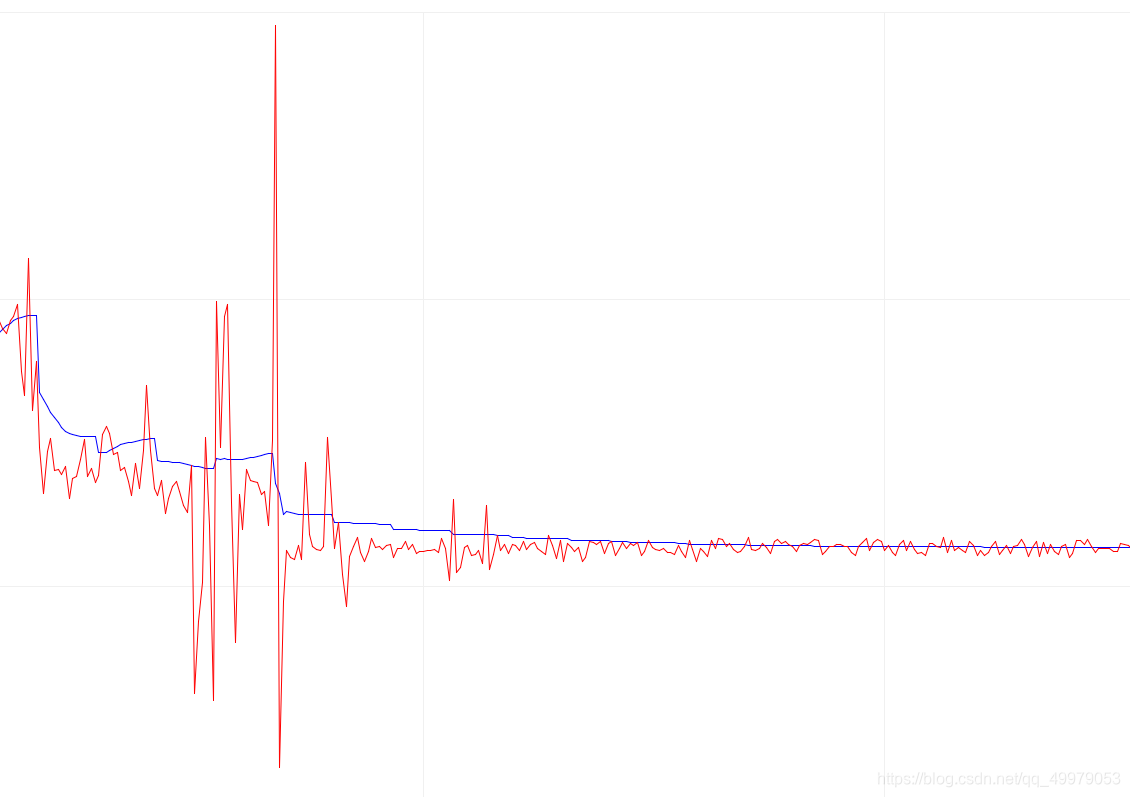
加速度解算后的 \(Pitch\)相对于\(DMP\)的输出值包含大量高频噪声,但是灵敏度大大提高,基本可以实时输出角度值。
(个人感觉还是\(DMP\)比较稳定)
同理可得
\(Roll=arctan\frac{aacy}{aacz}*57.2974\)
\(Yaw=arctan\frac{aacx}{aacy}*57.2974\)
由于\(yaw\)角为绕\(z\)轴旋转的角,陀螺仪平放时,accz近似为\(1g\)
而\(y\)和\(z\)上少有加速度分量,所以解算的\(yaw\)误差较大。
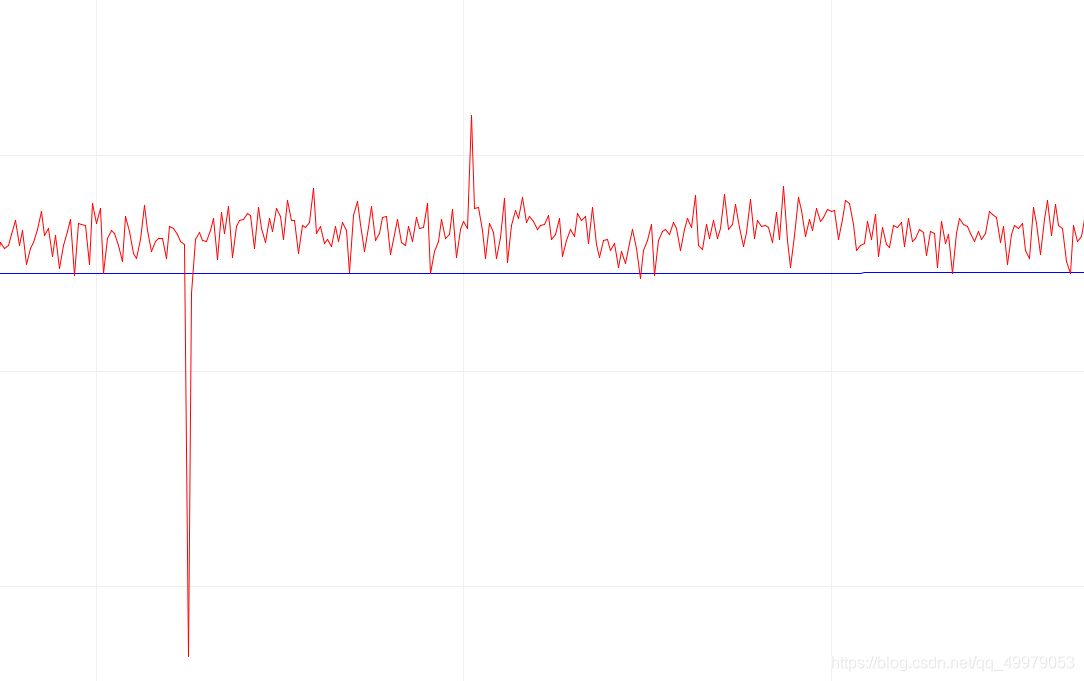
\(yaw\)的解算值与\(DMP\)输出波形的比较,通过输出曲线图可以看到解算后误差较大,且有大量高频噪声,一般不采用。
MPU6050角速度的解算
先看mpu角速度初始化的函数
//设置MPU6050陀螺仪传感器满量程范围
//fsr:0,±250dps;1,±500dps;2,±1000dps;3,±2000dps
//返回值:0,设置成功
// 其他,设置失败
u8 MPU_Set_Gyro_Fsr(u8 fsr)
{
return MPU_Write_Byte(MPU_GYRO_CFG_REG,fsr<<3);//设置陀螺仪满量程范围
}
根据寄存器在数据手册中找到相应的说明,

这里的\(LSB/(°/s)\)仍然是数据分辨率,
还是ADC读数数据
数据寄存器为16位,最高一位为符号位
即ADC输出范围为\(\pm32768\)
比如我们选中测量范围为\(\pm2000°/s\),
ADC读取的原始值为300
数据分辨率就是\(32768/2000=16.384 LSB/(°/s)\)
那么转换为角速度就是\(\frac{300}{16.384}=18.3105(°/s)\)
公式为:\(角速度=\frac{角速度原始值}{数据分辨率}\) 单位:\((°/s)\)
角速度已经推算出来了,
角度就可以通过对角速度的积分来计算(选取\(Pitch\)计算)
\(Pitch=\int \frac{gyrox}{角度分辨率}*dt\)
dt为我们读取mpu数据的间隔时间,
因为我们读取的数据是离散的,所以直接进行累加就可以计算角度
\(Pitch=\sum_1^n\frac{gyrox}{角度分辨率}*\Delta t\)
另外两个角的推算方法相同。
代码如下:
mpu_dmp_get_data(&pitch,&roll,&yaw); //得到姿态角即欧拉角
MPU_Get_Accelerometer(&aacx,&aacy,&aacz); //得到加速度传感器数据
MPU_Get_Gyroscope(&gyrox,&gyroy,&gyroz); //得到陀螺仪数据
Acc_Pitch=atan((float)aacx/(float)aacy)*57.297;
Gyro_Pitch+=-(gyrox/16.4)*0.01; //读取间隔为10ms转换为0.01s计算,读取数值与实际值相反加负号
printf("%f %f\r\n",pitch,Gyro_Pitch);
与\(DMP\)的输出波形相比,角速度积分的数据漂移比较明显,但数据的平滑性较好,可以有效抑制高频干扰。
互补滤波使用(数据融合)
| 对比项 | 加速度 | 陀螺仪(角速度) |
|---|---|---|
| 高频振动噪声 | 十分敏感 | 基本无感 |
| 高频低频姿态漂移 | 基本无感 | 飘移严重 |
| 实时性 | 实时性强,基本不会随时间飘移 | 随时间飘移严重 |
| 加速度数据,通过受力分能够显示角度变化趋势,在长期变化来看是可以利用的,实时性强。 |
角速度数据,加速度积分得到角度,但是由于传感器误差,积分作用会造成累计误差,所以角速度数据在短期是可以使用的,长期来看误差会很大是不可使用的。
数字低通滤波器
可以让长期变化通过(低频),滤波消除短期变化(高频),用于对加速度计的滤波。
数字高通滤波器
可以让短时信号通过(低频),过滤出变化缓慢的信号(高频),消除漂移。
我们截取陀螺仪解算数据的高频部分和加速度解算数据的低频部分进行融合,形成一个类似与模电的带通滤波器。
简单点就是陀螺仪低频不彳亍,我只要你的高频(短期)信号;
加速度的高频太抖了不彳亍,我就拿你的变化做个修正就\(OK\)了;
代码部分:
mpu_dmp_get_data(&pitch,&roll,&yaw); //得到姿态角即欧拉角
MPU_Get_Accelerometer(&aacx,&aacy,&aacz); //得到加速度传感器数据
MPU_Get_Gyroscope(&gyrox,&gyroy,&gyroz); //得到陀螺仪数据
Acc_Pitch=atan((float)aacx/(float)aacz)*57.297;
Gyro_Pitch=(gyrox/16.4)*0.01; //读取间隔为10ms转换为0.01s计算,读取数值与实际值相反加负号
Merge_Pitch=(Last_data+Gyro_Pitch)*(1-a)+a*Acc_Pitch;
Last_data=Merge_Pitch;
printf("%f %f\r\n",pitch,-Merge_Pitch);
\(MergePitch=(Lastdata+GyroPitch)*(1-a)+a*AccPitch\)
\(融合结果=(上次融合值+角速度一个采样周期的积分值)*(1-a)+a*加速度解算值\)
从代码中看出,角速度长时间容易飘移,我们就去一个周期的变化(高频)
加速度太抖,我们就拿你当成数据的修正(抑制高频),对数据进行更新。
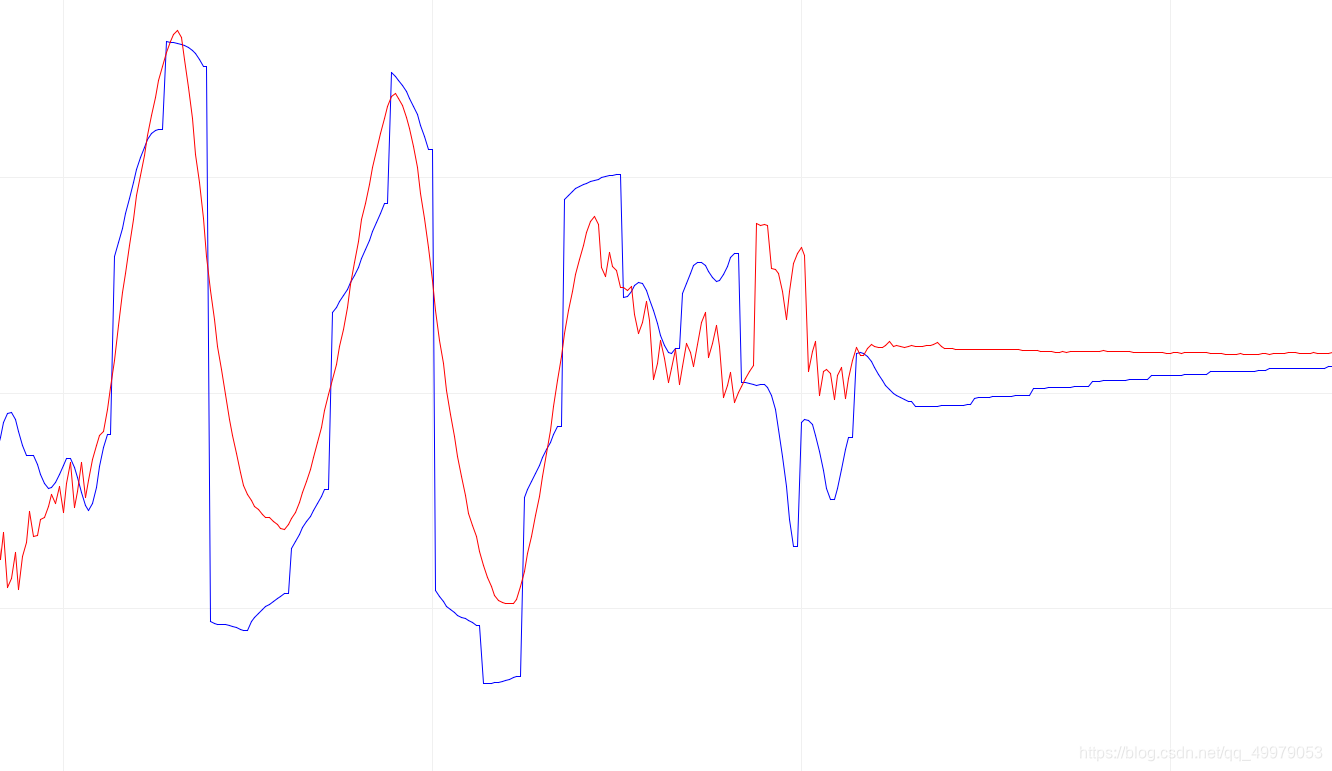
蓝色为\(DMP\)处理数据
红色为互补滤波融合后的数据
对比\(DMP\),互补滤波的平滑性更好,同时也具备灵敏度与实时性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号