【5分钟+】计算机系统结构-数据表示
计算机系统结构-数据表示
数据表示:数据表示是指能由计算机硬件直接识别和引用的数据类型。(例如定点数浮点数)
表现在什么地方:表现在它有对这种数据类型进行操作的指令和功能部件。
数据结构种类:串,队,列,栈,阵列,链表,树,图
什么是数据结构:它反映了应用中要用到的各种数据元素和或信息单元之间的结构关系。
数据表示
自定义数据表示
自定义数据表示,包括标志符的数据表示、数据描述符的数据表示。
标志符的数据表示
标识符的数据表示:指用于标识数据类型,例如负数、几机制、浮点型等;
原理:让计算机中每个数据都带有类型标志符。
优点:可简化指令系统和编译程序,便于不同数据类型的自动校验和检验。
缺点:一个标志位只能对一个数据进行描述。描述效率不高。
我们可以想象成 C# 中的值类型。
数据描述符的数据表示
跟标识符的数据表示类似,主要区别在于标识符的数据表示的标志符是跟数据在一起的;数据描述符的数据表示中,数据描述符是跟数据分开的。
数据描述符中包含数据的各种标志位、长度、数据地址。
我们可以想象成 C# 中的引用类型。
浮点数
对于一个浮点数,10进制情况下,我们可以使用以下公式表示小数部分
N = ±m * 10^e
N表示浮点数,m表示小数尾数,e表示位数。
例如 1100.1 = 0.1 * 10^3。
上面的是 10 进制情况下,而在计算机系统中,一般使用 2、8、16进制表示。
因此,计算机表示浮点数的公式如下
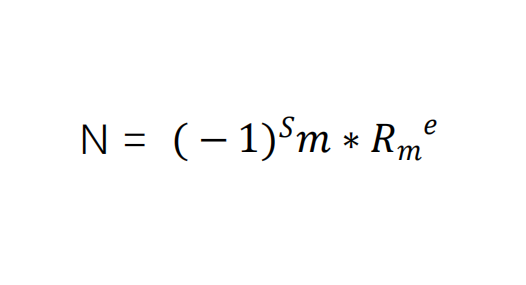
S 表示正负,S = 0时,N为正数,S = 1 时, N为负数。
m 为小数尾数。
Rm 表示阶码的基。
e 表示阶码的值。
浮点数在数据存储单元中的存储方式如图
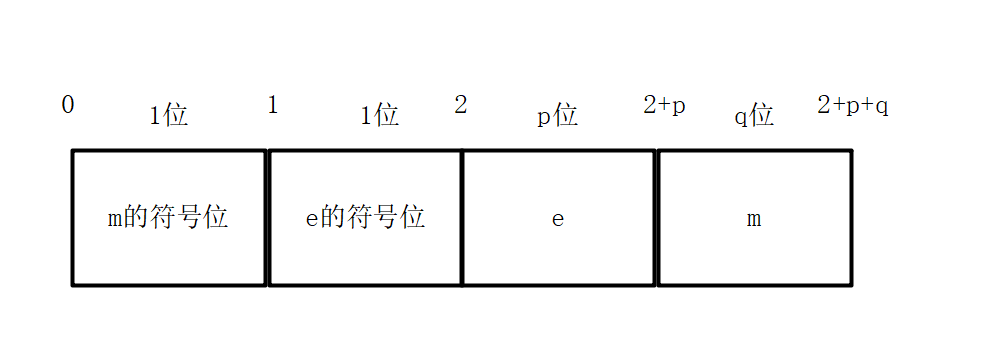
有些书籍和教程中, 将 er 和 e 位放到一起

浮点数的阶码需要移码。
出现上面的原理,只是将属于尾数的符号位(正负)放到了开头的位置。
原码:二进制数的最高一位代表正负符号,0代表正号,1代表负号,以下各位给出数值绝对值的表示法。
原理:(-1)S ,当 s = 0 时,值为正数;当 s = 1 时,值为负数。
零有正零和负零两种表示形式。
补码:将一个数转为原码后。
若为正数,数的补码和原码相同,不需要变换。
若为负数,除首位外,其余位取反,最后一位加 1。
零只有一种表示形式,即原码中的正零。
移码:移码(又叫增码)是符号位取反的补码,一般用指数的移码减去1来做浮点数,引入的目的是为了保证浮点数的机器码为全0。
移码与补码的符号位互为相反数。
例如将一个数 666666 转为 8 进制浮点数格式
666666(int) = 2426052 = 2.426052 * 8^6
以上可知,m = 0.2426052;rm = 8;e = 6;
八进制 2426052 的二进制为 00001010 00101100 00101010
6 的二进制 00000110;移码为 10000110。
合并起来就是 10000110 + 00001010 00101100 00101010
所以 666666 存储形式为 0100001100001010 00101100 00101010
要注意的是,实际计算是二进制的,上面的计算方法只是为了更加清晰理解表示方法。
可以看到,当位数一定时,阶码的位数越大,可以表示的范围越大,但是精度变低;
阶码的位数越小,可以表示的范围越小,但是精度更高。
浮点数标准
IEEE754 中,规定了单精确度(float)、双精确度(double) 两种基本浮点型
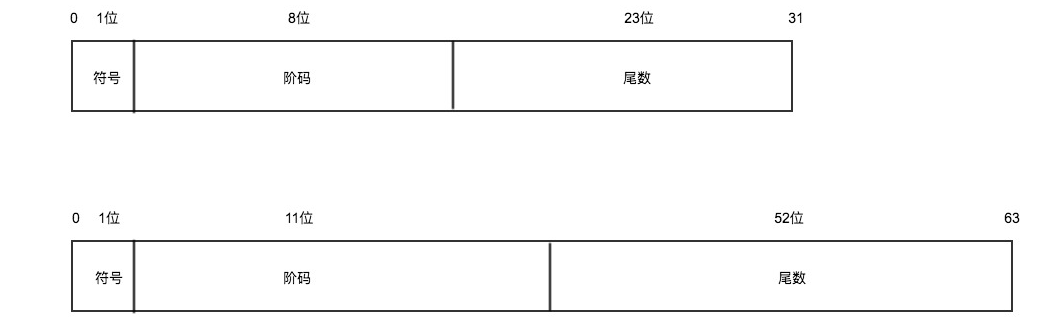
Float
那么阶码的值e 最大为 28-1 ,-127~128 (因为负数需要补码+1)。
rme = 2-127 ~ 2128
2128 是 rme 的最大绝对值。
所以上下限范围是 -3.4028236692094e+38 ~ 3.4028236692094e+38。
去除多余的小数,为 -3.40E+38 ~ +3.40E+38。
尾数范围 223 = 8388608,一共7位。
所以 Float 精确度只有 7 位。因为往往最后一位是四舍五入后的数,所以能完全保证准确度的只有 6 位。
例题
1,求 -666666 在 float 中存储的形式
解题过程:
将 -666666 转为 二进制 为 10001010 00101100 00101010 。因为负数需要补码,
所以 反码11110101 11010011 11010101,补码 11110101 11010011 11010110 。
回归正题,
-666666 = -11110101 11010011 11010110,
移动5位 = -1.1110101 11010011 11010110 * 223
e = 23,转为 二进制为存储数 0001 0111,移码 1001 0111。
最后 1 1001 0111 1110101 11010011 11010110 。
2,求 -6.66666 在 float 中存储的形式
将 6 转为二进制为 0000 0110
0.66666 转为二进制为 0.10101010101010100011101011010001100011010010010111111... ...
因为留给存储尾数的空间只有 24 位,6已经使用了一位,所以
0.66666 取16 位为 0.1010101010101010,其余精度丢失。
6.66666 转为二进制为 0000 0110 . 10101010 10101010
倒过来 110.1010101010101010 转为 10 进制为 6.666656494140625,精度发生变化。
-6.66666 原码 1000 0110 . 10101010 10101010
补码 1111 1001 . 01010101 01010111
小数点左移 7 位 1.111 1001 01010101 01010111
所以 6.66666 = 1.111 1001 01010101 01010111 * 27
7 转为二进制为 0000 0111,移码为 1000 0111
最后 1 1000 0111 111 1001 01010101 01010111
可以看到,上面已经发生精度丢失了。


