数据结构基础—树与二叉树(1)
数据结构基础—树和二叉树
一、树、二叉树类型定义
1.树的定义
a.定义
树是一种非线性结构,是具有相同特征的数据元素的集合(同质/类)
| 数据对象D:D是具有相同特征的数据元素的集合(同质/类) |
|---|
| 数据关系R: 若D为空树,则就角空树 否则 1. n = 1(一个元素),有且仅有一个根节点 2. n > 1,其余节点可分为m颗不相交的有限子集(小树)(递归定义),每一个子 集也叫一颗子树符合... |
| 基本操作:查找类,插入类(初始化,节点插入子树...),删除类(销毁.删除结点...) |
根是树的第一层,子树依次类推++
深度:最大的层数 = max(子树深度)+1(递归啦)
b.分类
- 有向树:有确定的根,自顶向下(一般)
- 有序树:子树之间存在有次序关系
- 无序树:子树之间不存在次序关系
c.对比树型结构和线性
- 线性:第一元素无前驱,最后一个元素无后继;其他元素一个前驱,一个后继
- 树型:根结点无前驱,多个叶子结点无后继;其他元素,一个前驱,多个后继
d.属性
结点:数据元素+若干指向子树的分支(结点关系)
结点的度:分支个数(子树棵树..)
树的度:树中所有结点的度的最大值
叶子结点:度为零的结点
分支结点:度>0的结点
路径:从根到某个结点的路线
同一层的都是堂兄弟,若父结点相同:兄弟结点
祖先结点:> 父结点的结点的统称
e.森林
m > 0棵不相交的树的集合(可以看成去了头结点...)
2.二叉树类型定义:
a.定义
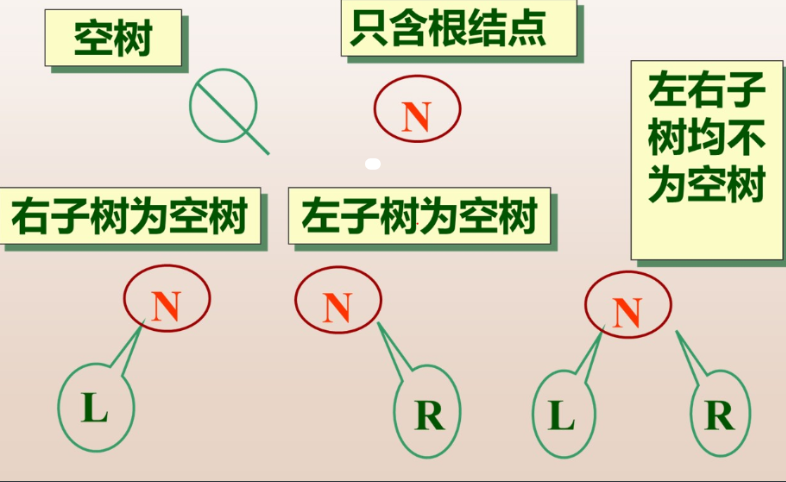
空树 / 一个根结点+两颗子树(还是二叉树)
是有序树,分左右子树
b.二叉树的5中形态
b.特殊的二叉树
-
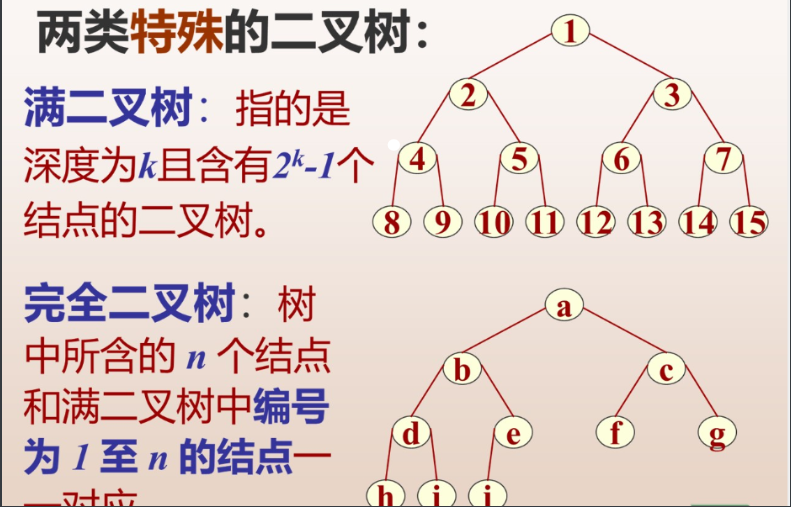
满二叉树,深度为k的树有2的k-1次方个结点
-
完全二叉树,满二叉树去掉右边的叶子不能跳的去。树中所含n个结点和满二叉树中编号1-n的结点一一一对应
c.完全二叉树性质
1.二叉树第i层最多2的n-1次方的结点(i >= 1)
2.若深度为i,则最多有多少个结点(等比求和),2的i次方 - 1
3.若深度为i,则,第i层最少1个结点。整个树最少有i个结点
4.结点和边(分支)的关系。n个结点,n-1个分支(n = e + 1)
5.叶子结点和度为2的关系:n0 = n2 +1(n=n0 + n1 + n2 = e(n1+n2) + 1)
6.完全二叉树有n个结点,则,深度为log2n取整数(向下取)+1
7.结点编号:结点为i,若i = 1是根结点,i/2是双亲。i >1且 2i <= n,左子2i;i >1且 2i+1 <= n,右2i+1
二、二叉树的存储结构
1.顺序
#define MaxSize 100
typefef TElemType SqbItREE[maxSzie];//零号单元存储根节点
SqBiTree bt;
只适用于完全二叉树好
2.链式
a.二叉链表
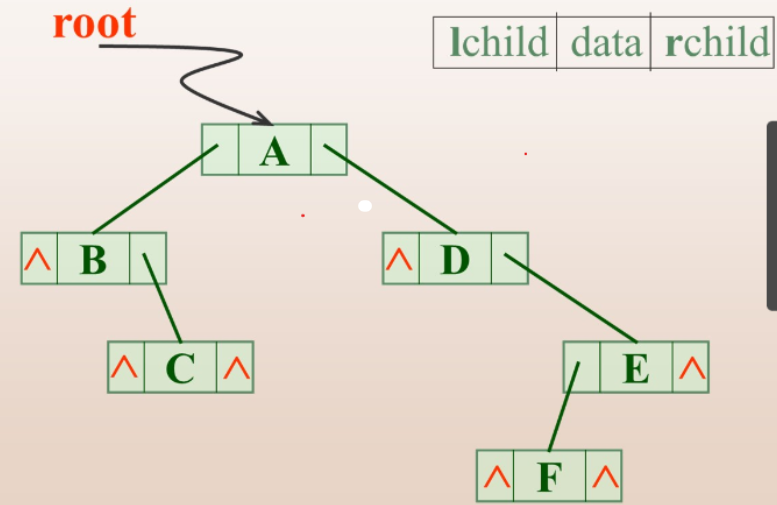
typedef struct BiTNode{
TElemType data;//数据
struct BiTNode *lchild,*rchild;//左右指针
}BiTNode,*BiTree;
n个结点的二叉链表中,有 n+1个空指针域(2n个指针域,除了根结点,每个结点对应一个,n-1个,2n- (n-1))
b.三叉链表
浪费一些空间
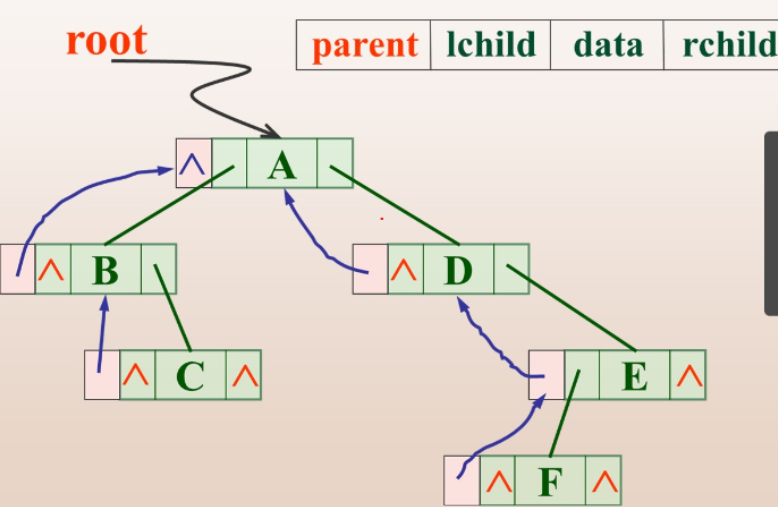
typedef struct TrTNode{
TElemType data;//数据
struct TrTNode *lchild,*rchild;//左右指针
struct TrTNode *parent;//双亲指针
}TrTNode,*TrTree;
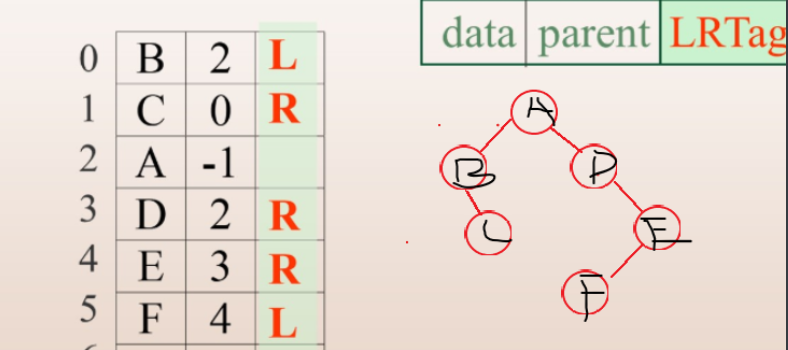
typedef struct BPTNode{//结点结构
TElemType data;//数据
int *parent;//指向双亲的指针
char *LRTag;//左右孩子的标志
}BPTNode;
typedef structBPTree{
BPTNode nodes[MaxSize];
int mum;结点数目
int root;跟结点的位置
}BPTree;
d.静态链表
三、二叉树的遍历
1.算法递归的描述
满足条件:
- 每一次调用更接近解
- 必须有一个终止处理或计算
递归一定可以改成栈
分治法,后置递归法,回溯法(与分治本本质相同)
尾递归(提倡简单,设计,效率高)
2.二叉树的遍历
a.遍历路径
对于二叉树,有三种遍历路径
先上后下的层次遍历,先左后右(正序),先右后左(逆序)
b.先左后右的遍历(正序)
分为三种:根左右(先),左根右(中),左右根(后)
先序描述
//递归
void Preorder(BiTree T,void(*visit)(TElemType& e)){//先序遍历
//对该结点的操作
if(T){
visit(T->data);//访问
Preorder(T->lchild,vist);//遍历左子树
// visit(T->data);中序
Preorder(T->lchild,vist);//遍历右子树
// visit(T->data);后序
}
}
其实,三种访问算法的实质是一样的,是指访问时机不同(沿着树画出线画出空结点)
- 先:第一次经过就访问
- 中:第二次经过就访问
- 后:第三次经过就访问
c.第一个结点和最后一个结点
第一个结点:
- 先序:根结点
- 中序:从根结点出发,沿左链走,第一个没有左孩子的结点
- 后序:在左链,沿着左链一直走,找到没有左孩子的结点;若该结点没有右孩子该结点就是最后一个结点;如果有右孩子则重复上述操作
最后一个结点:
- 先序:在右链,沿着右链一直走,找到没有右孩子的结点;若该结点没有左孩子该结点就是最后一个结点;如果有左孩子则重复上述操作
- 中序:从根结点出发,沿右链走,第一个没有右孩子的结点
- 后序:根结点
d.非递归遍历
代码放在下一篇啦(要不有点多)
总是先将树的左子入栈
用栈或者模拟栈均可
第一种
先获取第一个左链结点,并将其所有的根结点入栈(左结点全部入栈,除了获取的结点)
访问该结点,查询是否有右结点,如果有,重复上述;
如果没有,则判断栈(该结点的根结点是栈顶)是否空,不空:则退栈,获取该栈顶为新的"第一个结点",重复上述;空(遍历结束)
第二种
若栈或树不空时
- 树不空:树进栈,沿左链下移
- 栈不空:退一个栈到T,并获取T。T沿右链下移
四、二叉树的一些基本操作
和遍历一样放在下一篇了



