树状数组模板

单修区查

【模板】树状数组 1

题目描述

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $ x $

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 \(n,m\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 $ n$ 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。

接下来 \(m\) 行每行包含 \(3\) 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 \(x\) 个数加上 \(k\)

• 2 x y 含义：输出区间 \([x,y]\) 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 \(30\%\) 的数据，\(1 \le n \le 8\)，\(1\le m \le 10\)；
对于 \(70\%\) 的数据，\(1\le n,m \le 10^4\)；
对于 \(100\%\) 的数据，\(1\le n,m \le 5\times 10^5\)。

数据保证对于任意时刻，\(a\) 的任意子区间（包括长度为 \(1\) 和 \(n\) 的子区间）和均在 \([-2^{31}, 2^{31})\) 范围内。

样例说明：

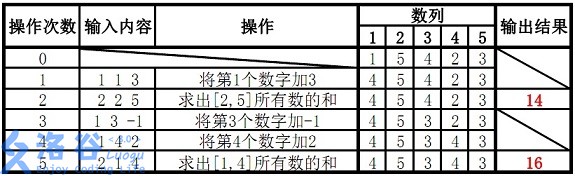
故输出结果14、16

Code

#include<bits/stdc++.h>
#define put(n) scanf("%lld",&n) 
#define out(n) printf("%lld\n",n)
#define ll long long
#define fd(a,b,c) for(ll a=b;a<=c;++a)
using namespace std;
int c[500100],n,m,num[500100],l,r;
char a;
int ask(int x)
{
	int ans=0;
	for(;x;x-=(x&-x)) ans+=c[x];
	return ans; 
}
void add(int x,int y)
{
	for(;x<=n;x+=(x&-x)) c[x]+=y;
}
int main()
{
//	freopen("sum.in","r",stdin);
//	freopen("sum.out","w",stdout);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>num[i];
		add(i,num[i]);
	}
	for(int i=1;i<=m;i++)
	{
		cin>>a>>l>>r;
		if(a=='1')
		{
			add(l,r);
			num[l]+=r;
		}
		else
		{
			cout<<(ask(r)-ask(l-1))<<endl; 
		}	
	}
	return 0;
}

区修单查

【模板】树状数组 2

题目描述

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 \(x\)；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 \(N\)、\(M\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(N\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。

接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)；

操作 \(2\)： 格式：2 x 含义：输出第 \(x\) 个数的值。

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

6
10

提示

样例 1 解释：

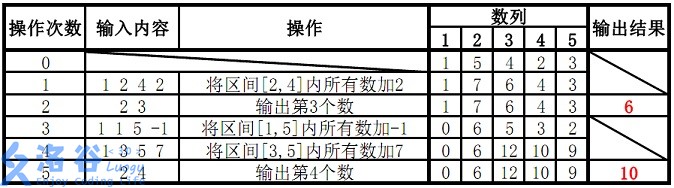
故输出结果为 6、10。

---

数据规模与约定

对于 \(30\%\) 的数据：\(N\le8\)，\(M\le10\)；

对于 \(70\%\) 的数据：\(N\le 10000\)，\(M\le10000\)；

对于 \(100\%\) 的数据：\(1 \leq N, M\le 500000\)，\(1 \leq x, y \leq n\)，保证任意时刻序列中任意元素的绝对值都不大于 \(2^{30}\)。

Code

#include<bits/stdc++.h>
#define put(n) scanf("%lld",&n) 
#define out(n) printf("%lld\n",n)
#define ll long long
#define fd(a,b,c) for(ll a=b;a<=c;++a)
using namespace std;
int c[500100],n,m,num[500100],l,r,k;
char a;
int ask(int x)
{
	int ans=0;
	for(;x;x-=(x&-x)) ans+=c[x];
	return ans; 
}
void add(int x,int y)
{
	for(;x<=n;x+=(x&-x)) c[x]+=y;
}
int main()
{
//	freopen("sum.in","r",stdin);
//	freopen("sum.out","w",stdout);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>num[i];
//		add(i,num[i]);
	}
	for(int i=1;i<=m;i++)
	{
		cin>>a;
		if(a=='1')
		{
			cin>>l>>r>>k;
			add(l,k);
			add(r+1,-k);
		}
		else
		{
			cin>>k;
			cout<<(ask(k)+num[k])<<endl; 
		}	
	}
	return 0;
}

树状数组找区间最大值（但是只能 \(1-n\)）

Code

struct ST
{
	int c[N<<1];
	
	inline void add(int x,int y)
	{
		for(;x<=lim;x+=(x&-x)) c[x]=max(c[x],y);
	}
	
	inline int ask(int x)
	{
		int res=-1e9;
		for(;x;x-=(x&-x)) res=max(c[x],res);
		return res;
	}
	
}st;

struct版本

Code

struct ST
{
	int c[N<<1];
	
	inline void add(int x,int y)
	{
		for(;x<=N;x+=(x&-x)) c[x]+=y;
	}
	
	inline int ask(int x)
	{
		int res=0;
		for(;x;x-=(x&-x)) res+=c[x];
		return res;
	}
	
}st;