【杂文】重新审视 ViT 中的 Token 表示
🚩前言
- 🐳博客主页:😚睡晚不猿序程😚
- ⌚首发时间:2023.6.2
- ⏰最近更新时间:2023.6.2
- 🙆本文由 睡晚不猿序程 原创
- 🤡作者是蒻蒟本蒟,如果文章里有任何错误或者表述不清,请 tt 我,万分感谢!orz
相关文章目录 :
1. 内容简介
ViT 的操作单位是 Token,也就是图像经过 Patch Embedding 之后生成的序列信息,序列信息和原本的图像表示有些联系。
本文分析了在 ViT 中引入 DWConv(depthwise convolution)的作用,以及 Token 表示与图像表示互相转化时的关系。
2. 在 ViT 中引入 DWConv
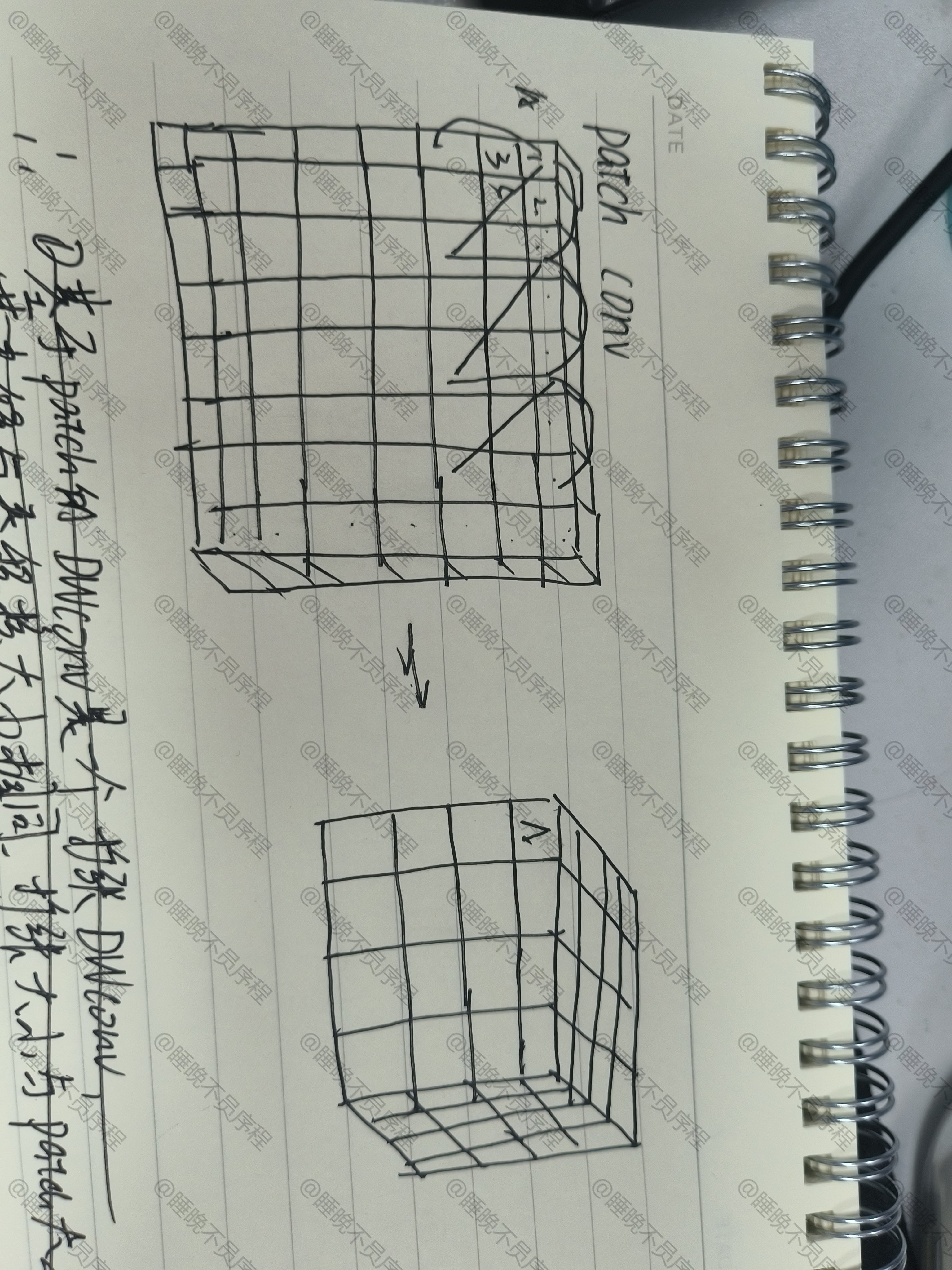
假设输入大小为 (8,8,1),也就是单通道的 8x8 图像,patch 大小为 2,经过了划分变为 (4,4,4),每一个像素被展平并级联
此时在上面做 2x2 步长为 1 的卷积 DWConv,实际上就是在原图像上做 2x2 ,步长为 1,间隔为 1 的扩张 DWConv
因为像素是按通道以此级联的,所以 DWConv 实际上也是在不同的通道上进行操作的
结论:
基于 Patch 的 DWConv 实际上可以看成是一个扩张卷积,他可以以一种高效的方式增大卷积核感受野,但是仍然会存在扩张卷积的问题
3. 对 Token 使用线性变换
如果要进行 Patch embedding,实际上可以划分为先划分 patch,展平,然后使用全连接层来进行 embedding
实际上这样就是一个大小等于 patch 大小,步长也等于 patch 大小的卷积——可以看作是一个下采样操作
此时如果我们希望将他还原成图像的表示,也就是重做 patch 划分的逆过程,这样实际上是一个 上采样操作,约等于是亚像素卷积
结论:
对 Token 做的线性变换可以看作是一次下采样,如果想要把 Token 重新变换回图像,可以看作是做了一次亚像素卷积,可能损失部分的空间信息
总结
- 每一次 patch embedding 都可以看成是一个下采样操作,如果将将其还原为图像,那么这次 embedding 操作实际上是在重新做了一次亚像素卷积来进行还原
- 在 ViT 中引入 DWConv,实际上就是使用了扩张卷积,基于 patch 的 DWConv 同理


