【手搓模型】亲手实现 Vision Transformer
🚩前言
- 🐳博客主页:😚睡晚不猿序程😚
- ⌚首发时间:2023.3.17,首发于博客园
- ⏰最近更新时间:2023.3.17
- 🙆本文由 睡晚不猿序程 原创
- 🤡作者是蒻蒟本蒟,如果文章里有任何错误或者表述不清,请 tt 我,万分感谢!orz
相关文章目录 :无
目录
1. 内容简介
最近在准备使用 Transformer 系列作为 backbone 完成自己的任务,感觉自己打代码的次数也比较少,正好直接用别人写的代码进行训练的同时,自己看着 ViT 的论文以及别人实现的代码自己实现一下 ViT
感觉 ViT 相对来说实现还是比较简单的,也算是对自己代码能力的一次练习吧,好的,我们接下来开始手撕 ViT
2. Vision Transformer 总览

我这里默认大家都理解了 Transformer 的构造了!如果有需要我可以再发一下 Transformer 相关的内容
ViT 的总体架构和 Transformer 一致,因为它的目标就是希望保证 Transformer 的总体架构不变,并将其应用到 CV 任务中,它可以分为以下几个部分:
-
预处理
包括以下几个步骤:
- 划分 patch
- 线性嵌入
- 添加 CLS Token
- 添加位置编码
-
使用 Transformer Block 进行处理
-
MLP 分类头基于 CLS Token 进行分类
上面讲述的是大框架,接下来我们深入 ViT 的Transformer Block 去看一下和原本的 Transformer 有什么区别
Transformer Block

和 Transformer 基本一致,但是使用的是 Pre-Norm,也就是先进行 LayerNorm 然后再做自注意力/MLP,而 Transformer 选择的是 Pose-Norm,也就是先做自注意力/MLP 然后再做 LayerNorm
Pre-Norm 和 Pose-Norm 各有优劣:
- Pre-Norm 可以不使用 warmup,训练更简单
- Pose-Norm 必须使用 warmup 以及其他技术,训练较难,但是完成预训练后泛化能力更好
ViT 选择了 Pre-Norm,所以训练更为简单
3. 手撕 Transformer
接下来我们一部分一部分的来构建 ViT,由一个个组件最后拼合成 ViT
3.1 预处理部分
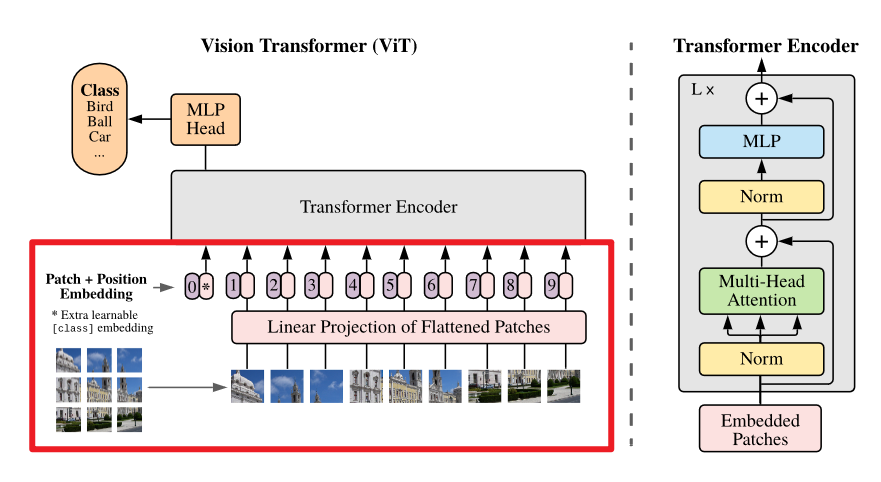
这一部分我们将会构建:
- 划分 patch
- 线性嵌入
- 插入 CLS Token
- 嵌入位置编码信息
我们先把整个部分的代码放在这里,之后我们再详细讲解
import torch
import torch.nn as nn
import torch.nn.functional as F
from einops import rearrange, repeat
from einops.layers.torch import Rearrange
class pre_proces(nn.Module):
def __init__(self, image_size, patch_size, patch_dim, dim):
super().__init__()
self.patch_size = patch_size
self.dim = dim
self.patch_num = (image_size//patch_size)**2
self.linear_embedding = nn.Linear(patch_dim, dim)
self.position_embedding = nn.Parameter(torch.randn(1, self.patch_num+1, self.dim)) # 使用广播
self.CLS_token = nn.Parameter(torch.randn(1, 1, self.dim)) # 别忘了维度要和 (B,L,C) 对齐
def forward(self, x):
x = rearrange(x, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=self.patch_size, p2=self.patch_size) # (B,L,C)
x = self.linear_embedding(x)
b, l, c = x.shape # 获取 token 的形状 (B,L,c)
CLS_token = repeat(self.CLS_token, '1 1 d -> b 1 d', b=b) # 位置编码复制 B 份
x = torch.concat((CLS_token, x), dim=1)
x = x+self.position_embedding
return x
可以先大概浏览一下,也不是很难看懂啦!
3.1.1 patch 划分
x = rearrange(x, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=self.patch_size, p2=self.patch_size) # (B,L,C)
我们直接使用 einops 库中的 rearrange 函数来划分 patch,我们输入的 x 的数组表示为 (B,C,H,W),我们要把它划分成 (B,L,C),其中 \(L=\frac W{W_p}\times \frac H{H_p}\),也就是 patch 的个数,最后 \(C=W_p\times H_p\times channels\)
这个函数就把原先的 (B,C,H,W) 表示方式拆开了,很轻易的就能够做到我们想要的 patch 划分,注意 h 和 p1 和 p2 的顺序不能乱
3.1.2 线性嵌入
首先我们要先定义一个全连接层
self.linear_embedding = nn.Linear(patch_dim, dim)
使用这个函数将 patch 映射到 Transformer 处理的维度
x = self.linear_embedding(x)
接着使用这个函数来执行线性嵌入,将其映射到维度 dim
3.1.3 插入 CLS Token
CLS Token 是最后分类头处理的依据,这个思想好像是来源于 BERT,可以看作是一种 池化 方式,CLS Token 在 Transformer 中会和其他元素进行交互,最后的输出时可以认为它拥有了所有 patch 信息,如果不使用 CLS Token 也可以选择平均池化等方式来进行分类
首先我们要定义 CLS Token,他是一个可学习的向量,所以需要注册为 nn.Parameter ,其维度和 Transformer 处理维度一致,以便于后面进行级联
self.CLS_token = nn.Parameter(torch.randn(1, 1, self.dim)) # 别忘了维度要和 (B,L,C) 对齐
我们得到了一个大小为 (1,1,dim) 的向量,但是我们的输入的是一个 batch,所以我们要对他进行复制,我们可以使用 einops 库中的 repeat 函数来进行复制,然后再进行级联
CLS_token = repeat(self.CLS_token, '1 1 d -> b 1 d', b=b) # 位置编码复制 B 份
x = torch.concat((CLS_token, x), dim=1)
其中 b 是 batch 大小
可以发现 einops 库可以很方便的进行矩阵的重排
3.1.4 嵌入位置信息
ViT 使用可学习的位置编码,而 Transformer 使用的是 sin/cos 函数进行编码,使用可学习位置编码显然更为方便
self.position_embedding = nn.Parameter(torch.randn(1, self.patch_num+1, self.dim)) # 使用广播
可学习的参数一定要注册为
nn.Parameter
向量的个数为 patch 的个数+1,因为因为在头部还加上了一个 CLS Token 呢,最后使用加法进行位置嵌入
x = x+self.position_embedding
好了每个模块都讲解完成,我们将他拼合
class pre_proces(nn.Module):
def __init__(self, image_size, patch_size, patch_dim, dim):
super().__init__()
self.patch_size = patch_size # patch 的大小
self.dim = dim # Transformer 使用的维度,Transformer 的特性是输入输出大小不变
self.patch_num = (image_size//patch_size)**2 # patch 的个数
self.linear_embedding = nn.Linear(patch_dim, dim) # 线性嵌入层
self.position_embedding = nn.Parameter(torch.randn(1, self.patch_num+1, self.dim)) # 使用广播
self.CLS_token = nn.Parameter(torch.randn(1, 1, self.dim)) # 别忘了维度要和 (B,L,C) 对齐
def forward(self, x):
x = rearrange(x, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=self.patch_size, p2=self.patch_size) # (B,L,C)
x = self.linear_embedding(x) # 线性嵌入
b, l, c = x.shape # 获取 token 的形状 (B,L,c)
CLS_token = repeat(self.CLS_token, '1 1 d -> b 1 d', b=b) # 位置编码复制 B 份
x = torch.concat((CLS_token, x), dim=1) # 级联 CLS Token
x = x+self.position_embedding # 位置嵌入
return x
3.2 Transformer
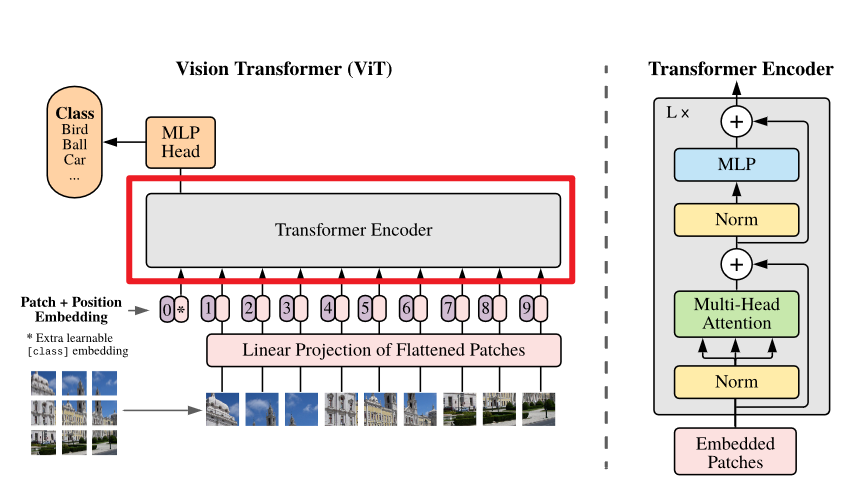
这一部分将会是我们的重点,建议大家手推一下自注意力计算,不然可能会有点难理解
3.2.1 多头自注意力
首先来回忆一下自注意力公式:
输入通过 \(W_q,W_k,W_v\) 映射为 QKV,然后经过上述计算得到输出,多头注意力就是使用多个映射权重进行映射,然后最后拼接成为一个大的矩阵,再使用一个映射矩阵映射为输出函数
还是一样,我们先把整个代码放上来,我们接着在逐行讲解
class Multihead_self_attention(nn.Module):
def __init__(self, heads, head_dim, dim):
super().__init__()
self.head_dim = head_dim # 每一个注意力头的维度
self.heads = heads # 注意力头个数
self.inner_dim = self.heads*self.head_dim # 多头自注意力最后的输出维度
self.scale = self.head_dim**-0.5 # 正则化系数
self.to_qkv = nn.Linear(dim, self.inner_dim*3) # 生成 qkv,每一个矩阵的维度和由自注意力头的维度以及头的个数决定
self.to_output = nn.Linear(self.inner_dim, dim)
self.norm = nn.LayerNorm(dim)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
x = self.norm(x) # PreNorm
qkv = self.to_qkv(x).chunk(3, dim=-1) # 划分 QKV,返回一个列表,其中就包含了 QKV
Q, K, V = map(lambda t: rearrange(t, 'b l (h dim) -> b h l dim', dim=self.head_dim), qkv)
K_T = K.transpose(-1, -2)
att_score = Q@K_T*self.scale
att = self.softmax(att_score)
out = att@V # (B,H,L,dim)
out = rearrange(out, 'b h l dim -> b l (h dim)') # 拼接
output = self.to_output(out)
return output
我们先用图来表示一下多头自注意力,也就是用多个不同的权重来映射,然后再计算自注意力,这样就得到了多组的输出,最后再进行拼接,使用一个大的矩阵来把多头自注意力输出映射回输入大小
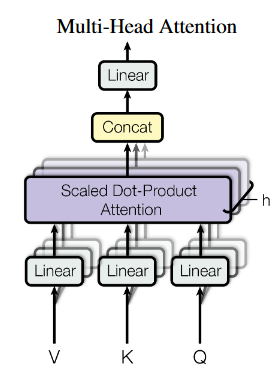
我们如何构造这多个权重矩阵来进行矩阵运算更快呢?答案是——写成一个线性映射,然后再通过矩阵重排来得到多组 QKV,然后计算自注意力,我们来看图:
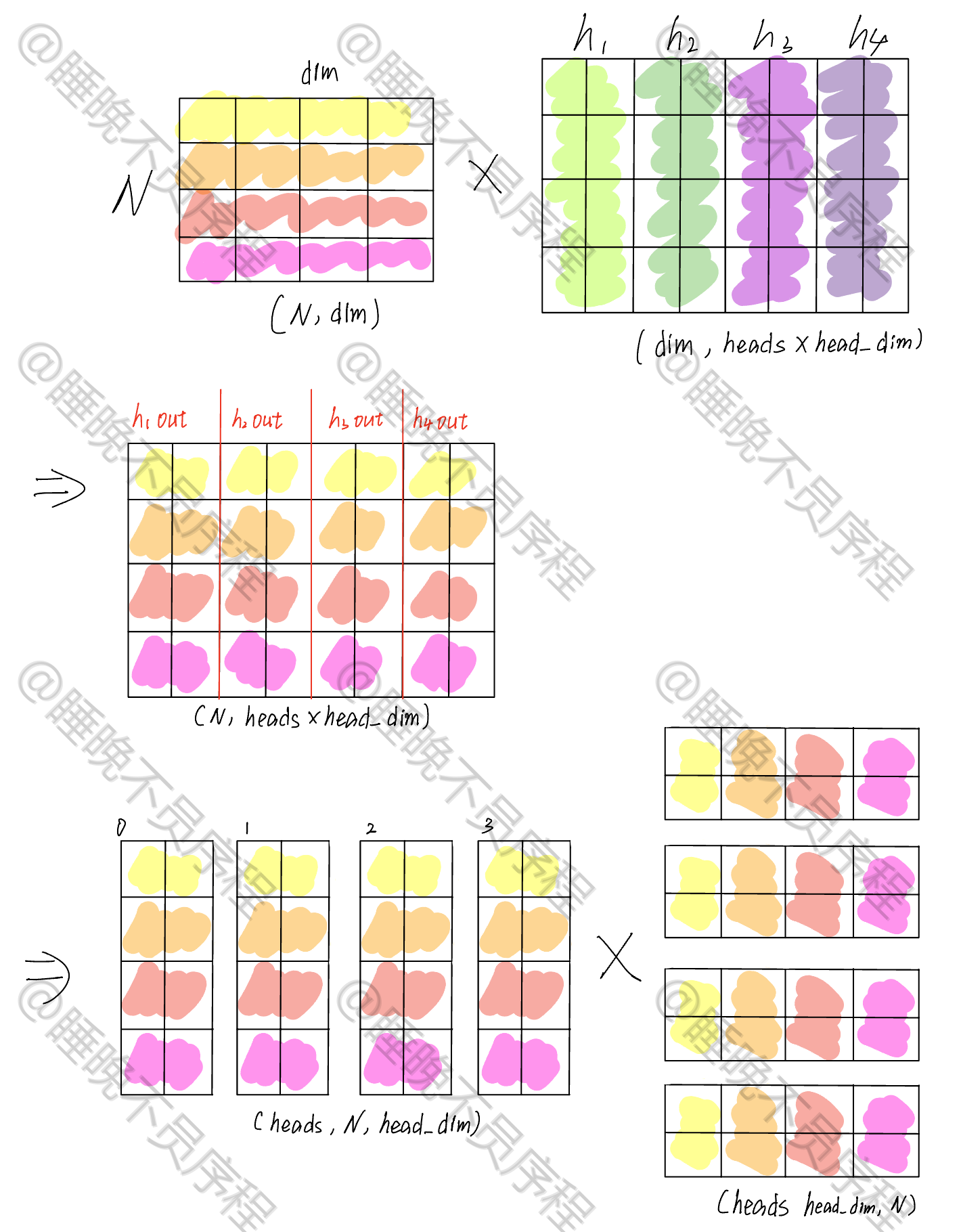
首先输入是一个 (N,dim) 的张量,我们可以把多头的映射横着排列变成一个大矩阵,这样使用一次矩阵运算就可以得到多个输出
我这里假设了四个头,并且每一个头的维度是 2
经过映射,我们得到了一个 \((N,heads\times head\_dim)\) 大小的张量,这时候我们对其重新排列,形成 \((heads,N,head\_dim)\) 大小的张量,这样就把每一个头给分离出来了
接着就是做自注意力,我们现在的张量当作 Q,K 就需要进行转置,其张量大小是 \((heads,head\_dim,N)\) ,二者进行相乘,得到的输出为 \((heads,N,N)\),这就是我们的注意力得分,经过 softmax 就可以和 V 相乘了
这里省略了 softmax,重点看矩阵的维度变化
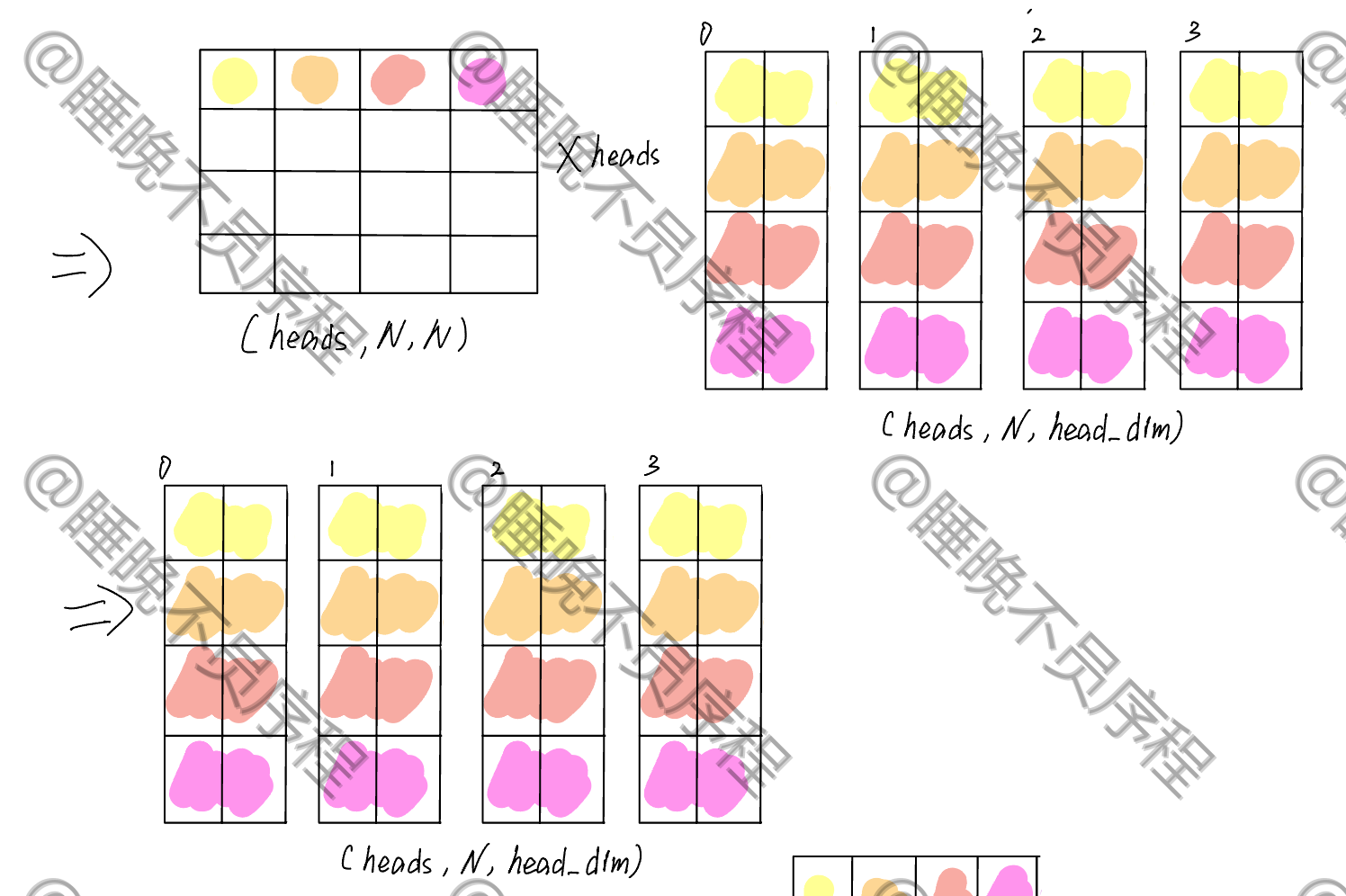
计算自注意力输出,就是和 V 相乘,V 的张量大小为 \((heads,N,head\_dim)\) ,最后得到输出大小为 \((heads,N,head\_dim)\)
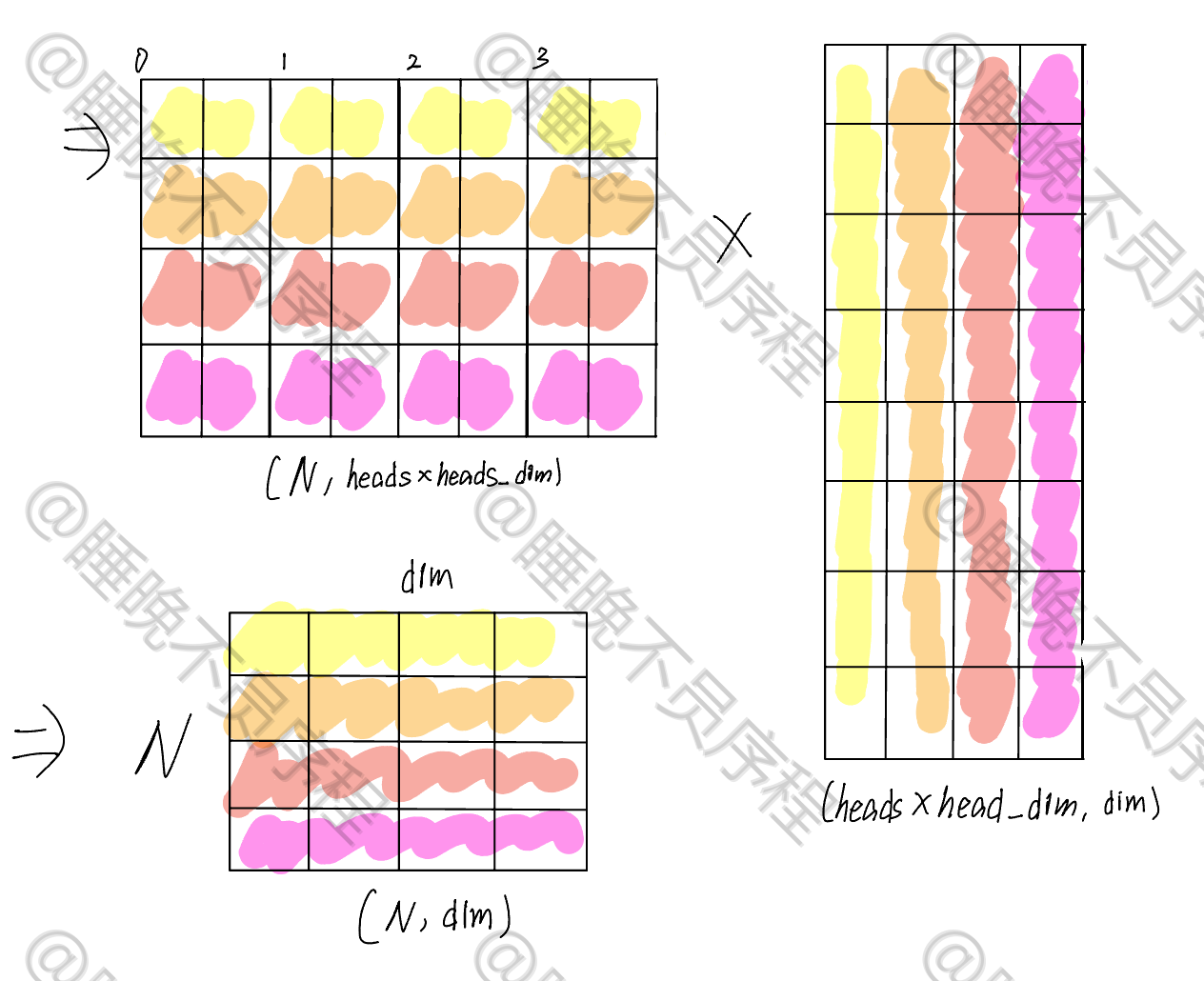
我们把上一步的张量 \((heads,N,head\_dim)\) 重排为 \((N,heads\times head\_dim)\),然后使用一个大小为 \((heads\times\_dim,dim)\) 的矩阵映射回和输入相同的大小,这样多头自注意力就计算完成了
大家可以像我一样把过程给写出来,可以清晰非常多,接下来我们再看一下代码实现:
首先定义我们需要的映射矩阵以及 softmax 函数以及 layernorm 函数
self.head_dim = head_dim # 每一个注意力头的维度
self.heads = heads # 注意力头个数
self.inner_dim = self.heads*self.head_dim # 多头自注意力输出级联后的输出维度
self.scale = self.head_dim**-0.5 # 正则化系数
self.to_qkv = nn.Linear(dim, self.inner_dim*3) # 生成 qkv,每一个矩阵的维度由自注意力头的维度以及头的个数决定
self.to_output = nn.Linear(self.inner_dim, dim) # 输出映射矩阵
self.norm = nn.LayerNorm(dim) # layerNorm
self.softmax = nn.Softmax(dim=-1) # softmax
有了这些,我们可以开始 MHSA 的计算
def forward(self, x):
x = self.norm(x) # PreNorm
qkv = self.to_qkv(x).chunk(3, dim=-1) # 按照最后一个维度均分为三分,也就是划分 QKV,返回一个列表,其中就包含了 QKV
Q, K, V = map(lambda t: rearrange(t, 'b l (h dim) -> b h l dim', dim=self.head_dim), qkv) # 对 QKV 的多头映射进行拆分,得到(B,head,L,head_dim)
K_T = K.transpose(-1, -2) # K 进行转置,用于计算自注意力
att_score = Q@K_T*self.scale # 计算自注意力得分
att = self.softmax(att_score) # softmax
out = att@V # (B,H,L,dim); 自注意力输出
out = rearrange(out, 'b h l dim -> b l (h dim)') # 拼接
output = self.to_output(out) #输出映射
return output
上面的部分进行组合
class Multihead_self_attention(nn.Module):
def __init__(self, heads, head_dim, dim):
super().__init__()
self.head_dim = head_dim # 每一个注意力头的维度
self.heads = heads # 注意力头个数
self.inner_dim = self.heads*self.head_dim # 多头自注意力最后的输出维度
self.scale = self.head_dim**-0.5 # 正则化系数
self.to_qkv = nn.Linear(dim, self.inner_dim*3) # 生成 qkv,每一个矩阵的维度和由自注意力头的维度以及头的个数决定
self.to_output = nn.Linear(self.inner_dim, dim)
self.norm = nn.LayerNorm(dim)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
x = self.norm(x) # PreNorm
qkv = self.to_qkv(x).chunk(3, dim=-1) # 划分 QKV,返回一个列表,其中就包含了 QKV
Q, K, V = map(lambda t: rearrange(t, 'b l (h dim) -> b h l dim', dim=self.head_dim), qkv)
K_T = K.transpose(-1, -2)
att_score = Q@K_T*self.scale
att = self.softmax(att_score)
out = att@V # (B,H,L,dim)
out = rearrange(out, 'b h l dim -> b l (h dim)') # 拼接
output = self.to_output(out)
return output
3.2.2 FeedForward
构建后面的 FeedForward 模块,这个模块就是一个 MLP,中间夹着非线性激活,所以我们直接看代码吧
class FeedForward(nn.Module):
def __init__(self, dim, mlp_dim):
super().__init__()
self.fc1 = nn.Linear(dim, mlp_dim)
self.fc2 = nn.Linear(mlp_dim, dim)
self.norm = nn.LayerNorm(dim)
def forward(self, x):
x = self.norm(x)
x = F.gelu(self.fc1(x))
x = self.fc2(x)
return x
3.2.3 Transformer Block
有了 MHSA 以及 FeedForward,我们可以来构建 Transformer Block,这是 Transformer 的基本单元,只需要把我们构建的模块进行组装,然后添加残差连接即可,不会很难
class Transformer_block(nn.Module):
def __init__(self, dim, heads, head_dim, mlp_dim):
super().__init__()
self.MHA = Multihead_self_attention(heads=heads, head_dim=head_dim, dim=dim)
self.FeedForward = FeedForward(dim=dim, mlp_dim=mlp_dim)
def forward(self, x):
x = self.MHA(x)+x
x = self.FeedForward(x)+x
return x
添加了一个参数
depth,用来定义 Transformer 的层数
ViT
祝贺大家,走到最后一步啦!我们把上面的东西组装起来,构建 ViT 吧
class ViT(nn.Module):
def __init__(self, image_size, channels, patch_size, dim, heads, head_dim, mlp_dim, depth, num_class):
super().__init__()
self.to_patch_embedding = pre_proces(image_size=image_size, patch_size=patch_size, patch_dim=channels*patch_size**2, dim=dim)
self.transformer = Transformer(dim=dim, heads=heads, head_dim=head_dim, mlp_dim=mlp_dim, depth=depth)
self.MLP_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, num_class)
)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
token = self.to_patch_embedding(x)
output = self.transformer(token)
CLS_token = output[:, 0, :] # 提取出 CLS Token
out = self.softmax(self.MLP_head(CLS_token))
return out
总结
这里我们手动实现了 ViT 的构建,不知道大家有没有对 Transformer 的架构有更深入的理解呢?我也是动手实现了才理解其各种细节,刚开始觉得自己不可能实现,但是最后还是成功的,感觉好开心:D
参考
[2] 全网最强ViT (Vision Transformer)原理及代码解析
[3] Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16x16 words: Transformers for image recognition at scale[J]. arXiv preprint arXiv:2010.11929, 2020.


