【CS231n assignment 2022】Assignment2 - Part 1，全连接网络的初始化以及正反向传播

文章目录

• 前言
• • FullyConnectedNets
  • • 网络初始化
    • • 代码注意事项
      • • 1. W 的尺寸怎么知道？
        • 2. np.random.norml()
        • 3. batchnorm
    • loss(self, X, y=None)：
    • • 前向传播
      • • 代码注意事项
        • • 1. caches
          • 2. affine_relu_forward(x,W,b)
          • 3. for i in range(self.num_layers-1)
      • 反向传播
      • • 代码注意事项
        • • 1. 正则惩罚项
          • 2. 梯度计算
    • Initial Loss and Gradient Check
    • • 1. 用初始值来进行检查
      • 2. 利用小数据集进行检查
      • Inline Question 1：

---

前言

上周忘记更新了，作业也已经做了大半，作业二即将结束，现将整理的题解上传至博客，供大家参考🙂，有问题尽可滴滴博主哦~
本次更新内容为作业2中全连接网络的初始化以及正反向传播，作业二打算分为3~4次更新完成，避免一篇文章中内容过多（这是好处还是坏处呢？）
所有代码我均上传到 github 上了，欢迎交流~
好了，让我们开始吧！

作者：睡晚不猿序程
时间：2022.7.21

---

FullyConnectedNets

首先我们先完成全连接网络，这项作业在作业1中我们有实现过部分
按照题目指示，我们需要在 cs231n/layers.py中复用我们上一次作业所写的代码，所以我们打开 layers.py，将我们作业一的代码复制进来即可：

affine_forward

x_vector = x.reshape(x.shape[0], -1)
out = x_vector.dot(w)
out += b

affine_backward

dx = dout.dot(w.T).reshape(x.shape)
x_vector = x.reshape(x.shape[0], -1)
# print(dx.shape)
dw = x_vector.T.dot(dout).reshape(w.shape)
db = np.sum(dout, axis=0)  # 注意画图

relu_forward

out = np.reshape(x, (x.shape[0], -1))  # 先把他拆分成单个向量
out = np.maximum(0, x)
out.reshape(x.shape)

relu_backward

mask = np.int64(x > 0)
dx = dout * mask

softmax_loss

num_train = x.shape[0]
scores = x - np.max(x, axis=1, keepdims=True)  # 进行平移
f = np.exp(scores)  # 用e进行归一化
normalized_f = f / np.sum(f, axis=1, keepdims=True)
loss = np.sum(-np.log(f[range(num_train), y] /
                      np.sum(f, axis=1))) / num_train

normalized_f[range(num_train), y] -= 1
dx = normalized_f / num_train

分别在对应的位置粘帖上之前的代码即可，如上👆

---

网络初始化

接下来按照题目要求，我们打开 cs231n/classifiers/fc_net.py，查看我们需要完成的内容
其中给出了网络结构：
每一层网络由这几部分组成：全连接层- BN 层 - ReLU - dropout
但是最后一层的网络将会是一个全连接层+softmax

了解了这些，我们来看一下输入部分
hidden_dims一个列表，包含了每个隐藏层的大小
input_dim：输入的维度
num_classes：分类数
dropout_keep_ratio：位于(0,1)的范围之间，表示了 dropout 的强度
normalization：是否进行归一化，且有三种方式：批归一化，层归一化，不归一化
reg：正则化强度
weight_scale：初始化权重时的标准差
dtype：一个numpy的数据类型对象
seed：如果非空，就把这个随机种子用在dropout层

接着查看一下初始化的要求：

• 全部的参数保存于 self.params 字典
  • 命名为W1，b1
• 权重从均值为0，方差为 weight_scale 的标准正态分布中取出
• 偏移量初始化为0
• 当使用 BN 时候，把放缩因子保存下来
  • scale parameter设置为1
  • shift parameter设置为0

# 维度数组进行拼接
layer_dims = np.hstack((input_dim, hidden_dims, num_classes))

# 初始化W和b
for i in range(self.num_layers):
    W = np.random.normal(loc=0.0, scale=weight_scale, size=(layer_dims[i], hidden_dims[i+1]))
    b = np.zeros(hidden_dims[i+1])
    self.params['W' + str(i+1)] = W
    self.params['b'+str(i+1)] = b

if normalization == 'batchnorm':
    for i in range(self.num_layers-1):
        gamma = np.ones(layer_dims[i+1])
        beta = np.zeros(layer_dims[i+1])
        self.params['gamma'+str(i+1)] = gamma
        self.params['beta'+str(i+1)] = beta

代码注意事项

首先，已知网络的层数，我们可以优先初始化 W 和 b

1. W 的尺寸怎么知道？

在 layer_dims[] 数组中存放着隐藏层的大小，$W_i$的尺寸为（当前隐藏层大小，下一隐藏层大小）【原因：全连接】

2. np.random.norml()

从一个自己定义的正态分布中取值来进行赋值，主要参数有以下几个：
loc：该分布的均值，按照要求应该取0
scale：该分布的方差，按照要求应该取 weight_scale
size：赋值生成的 numpy 数组大小

3. batchnorm

如果使用 bath_nomalization，每一层的 BN 层将会增加两个可训练参数，分别为 gamma 和 beta，
他们均为向量，和当前的隐藏层维度相同，一个赋值为全1一个赋值为全0

在这里我们暂时不考虑给网络添加 BN 层以及 dropout 层，在之后的学习中我们会添加这一块，所以接下来有关 BN 层的和 dropout 层的内容我们都可以先不用看，我们先看单纯使用全连接网络的前向传播，位于函数 loss() 中

---

loss(self, X, y=None)：

在这个函数中，我们要完成网络的前向传播，然后计算得分并得到损失，然后使用反向传播得到对应的梯度
首先我们先来看函数的输入以及返回
输入：

• X，图像矩阵
• y，标签数组

返回值：

• y如果是空，执行一次前向传播并返回分数
  • scores：是一个（N，C）矩阵，代表着 N 张图片分别对应 C 个类别的得分
• y非空，执行训练时候的前向传播与反向传播，并返回
  • loss：损失值（一个数）
  • grads：梯度（是一个字典，保存了所有可学习参数的梯度）
    

前向传播

我们一步一步来，要得到分数首先要进行前向传播，代码如下

x=X
caches=[]   # 保存有网络的中间信息
for i in range(self.num_layers-1):
    W=self.params['W'+str(i+1)]
    b=self.params['b'+str(i+1)]

    # 无 BN，无 dropout
    if self.normalization == None:
        out,cache=affine_relu_forward(x,W,b)

    # 保存
    caches.append(cache)# 保存了当前层的输入信息
    x=out

scores,cache=affine_forward(x,self.params['W'+str(self.num_layers)],self.params['b'+str(self.num_layers)])
caches.append(cache)    # 保存了最后一层的输入信息，为(x,w,b)

代码注意事项

1. caches

首先判断一下我们需要什么信息，我们有了一个输入 X，我们自身 self 中的 params 中保存有网络的权重信息，我们还需要一个 caches 元组来保存网络前向传播中的中间信息以便于之后进行反向传播。所以我们选择新建一个caches

2. affine_relu_forward(x,W,b)

该函数已经在 layers_utils.py 中提供给我们，该文件中还有许多我们接下来会用到的函数，记得去认真查看一下它的 API

3. for i in range(self.num_layers-1)

为什么这里有个 -1 ，因为最后一层是没有 BN 或者是 dropout 的，所以需要拉出来单独计算

反向传播

实现了前向传播代码，我们接下来要实现反向传播代码，刚开始的时候我一直觉得反向传播是很有难度的，还是需要自己理顺

loss,dscores=softmax_loss(scores,y)	# 计算损失（不完整）以及反向传播过来的梯度
for i in range(self.num_layers):	# 一定要记得加上L2正则惩罚项，这样就计算得到完整的损失了
    W=self.params['W'+str(i+1)]
    loss+=0.5*self.reg*np.sum(W**2)

# 计算最后一层传播过来的梯度
dout,dW,db=affine_backward(dscores,caches[self.num_layers-1])
dW+=self.reg*self.params['W'+str(self.num_layers)]

grads['W'+str(self.num_layers)]=dW
grads['b'+str(self.num_layers)]=db

# 计算前n-1层的梯度
for i in range(self.num_layers-2,-1,-1):
    if self.normalization == None:
        dout,dW,db=affine_relu_backward(dout,caches[i])
        dW+=self.reg*self.params['W'+str(i+1)]
        grads['W'+str(i+1)]=dW
        grads['b'+str(i+1)]=db

代码注意事项

1. 正则惩罚项

直接调用函数计算 loss 很开心，但是之后忘记加上正则项结果答案不对就不开心了

2. 梯度计算

因为我们需要调用函数进行计算，最后一层就是一个全连接加上softmax了，所以我们把他拉出来单独计算，接下来在用一个for循环一次从后往前计算梯度。

经过了上面的步骤，我们可以执行第一个 cell 了
我们运行开始运行 Initial Loss and Gradient Check 部分

---

Initial Loss and Gradient Check

1. 用初始值来进行检查

我们初始化网络，然后看损失值是否在我们的预测范围内，即可知道我们的损失函数以及初始化参数是否正确



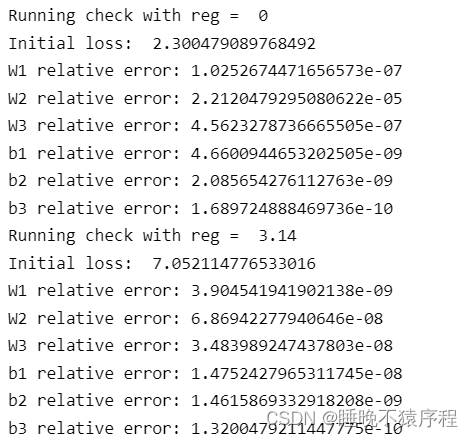
我们分别使用 reg = 0 以及 reg = 3.14 的情况来进行判断，结果分别于 2.3 以及 7 附近，没毛病，其他的值也在误差范围内。

2. 利用小数据集进行检查

我们使用一个含有 50 张图片的小数据集，使用三层网络，且隐层单元均为100，接着调整 learning_rate 和 weight_initialization_scale 使其在 20 epochs 之内完成过拟合。如果可以完成，说明我们的模型可以训练
我们让 weight_scale = 2e-2，learning_rate = 1e-2，成功让让模型过拟合。



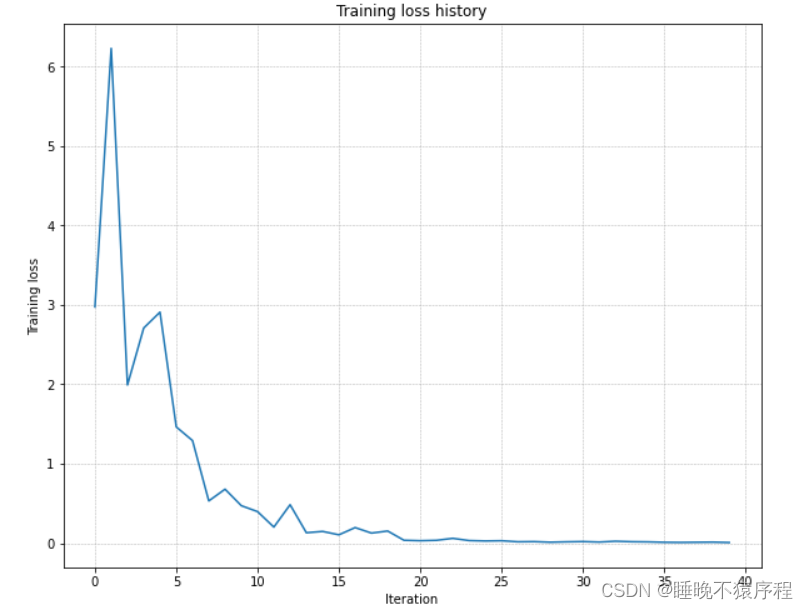
接下来我们要使用隐层维度为 100 的五层神经网络，在 50 张图片上在 20 个 epochs 之内完成过拟合。
我们调整让 weight_scale = 1e-3，learning_rate = 1e-1，成功完成过拟合，训练损失图如下：

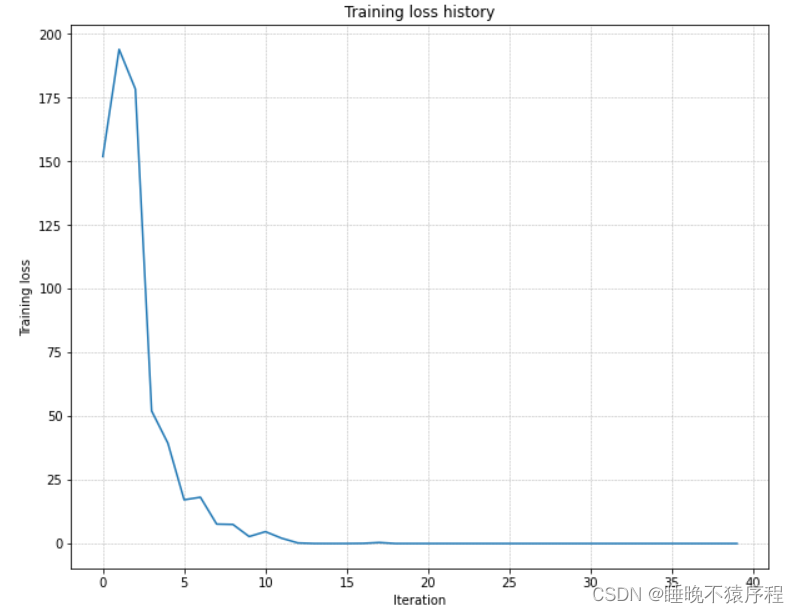
Inline Question 1：

【问】您是否注意到训练三层网络与训练五层网络的相对难度？特别是，根据您的经验，哪个网络似乎对初始化规模更敏感？你认为为什么会这样？

【答】发现了五层神经网络的训练难度更大，且对初始化规模更为敏感，我认为应该是因为网络的加深，使得参数增多，对扰动更加敏感