1、回归 一元线性回归 代价函数 梯度下降法

 

1、回归是达尔文表弟发现的，就是说人类总体有一个平均身高。那个高个子生的孩子都个高，矮的孩子生的矮。但是他们的下一代大部分都往平均身高长，也就是说特别高的人，他们的孩子会很高，但是往往比他们自己矮。特别矮的人他们生的孩子会矮一些，但是会比自己的父母高，他们都有这种趋势。表弟管这个叫做回归。

2、一元线性回归 指的是一个自变量对应一个因变量的 一元函数。当平面坐标系中 有些散列的点的时候，我们往往想找到一条直线去拟合他们的回归线。我们管这条直线叫做一元线性回归

 

 

假定这个函数为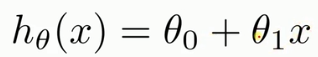我们要求的就是这个函数的和的值 确定了这个值 我们就确定了一元线性回归函数 

 

3、代价函数等于

 

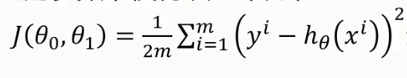
很显然 如果的值能使得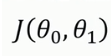最小 那就是我们要的一元线性回归函数。

 

4、梯度下降法

就是针对代价函数 的两个变量求偏微分，然后这个偏微分的值乘以一个变量 让当前导数的值-变量*学习量。值最小时就是梯度下降法所要的。此时的参数

 

 就是我们一元线性回归方程需要的两个值。关于学习变量 不要把它想得很神秘 拿到坐标系去研究  它只是为了配合求导的斜率 改变当前变量在坐标系上移动的方向和大小的 仅此而已

 

 

发散一下  如果不是 - 而是+ 的话就是求峰值 此时代价函数最大 拟合的最不好

另外有一点 为什么不用微积分中两次求导数 的方法求极值