DS博客作业02--栈和队列
| 这个作业属于哪个班级 |
| ---- | ---- | ---- |
| 这个作业的地址 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 吴慧敏 |
🔅0.PTA得分截图
🔅1.本周学习总结（0-5分）
1.1 栈
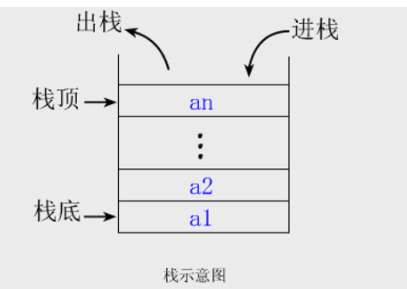
栈的定义：栈是一种只能在一端进行插入或删除操作的线性表。表中允许进行插入，删除操作的一端称为栈顶。
栈的进栈（插入操作）出栈（删除操作）规则：
出栈顺序：栈顶出栈（删除操作），栈底最后出栈，先进后出（Last In First Out）。
时进时出：元素未完全进栈时，即可出栈。
1.1.1顺序栈
顺序栈的结构
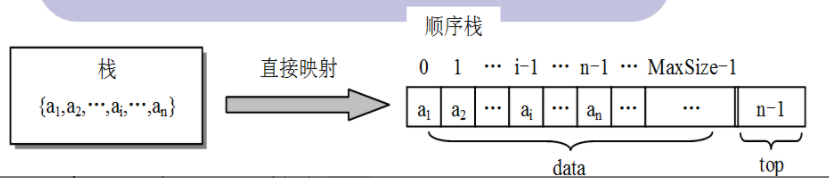
假设栈的元素个数最大不超过正整数MaxSize，所有的元素都具有同一数据类型ElemType，则栈类型SqStack：
typedef struct
{ ElemType data[MaxSize];
int top; //栈顶指针
} Stack;
tupedef Stack *SqStack;
- 顺序栈的4要素：
1.栈空条件：top=-1
2.栈满条件：top=MaxSize-1；
3.进栈e操作：top++；st->data[top]=e
4.退栈操作：e=st->data[top];top++;注意：栈内元素没删除
顺序栈的操作函数
1）初始化栈initStack（&s）
void InitStack(S)
{ s=new Stack;
s->top=-1;
}
2）销毁栈ClearStack（&s）
void DestroyStack(Stack &s)
{
delete s;
}
3）判断栈是否为空StackEmpty（s）
bool StackEmpty(SqStack s)
{
return (s->top==-1);
}
4)进栈Push（&s，e）
在栈不满的条件下，先将栈指针增1，然后在该位置上插入元素e。对应算法如下：
bool Push(SqStack &s,ElemType e)
{
if(s->top==MaxSize-1)//顺序栈务必考虑栈满
return false;
s->top++; //栈顶指针增1
s->data[s->top]=e;
return true;
}
5）出栈Pop（&s，&e）
在栈不为空的条件下，先将栈顶元素赋给e，然后将栈指针减1.对应算法如下：
bool Pop(SqStack &s,ElemType &e)
{
if(s->top==-1)//栈为空的情况，栈下溢出
return false；
e=s->data[s->top];//取栈顶指针元素
s->top--；//栈顶指针减1
return true；
}
6）取栈顶元素GetTop（s）
在栈不为空的情况下，将栈顶元素赋给e。
bool GetTop(SqStack *s,ElemType &e)
{
if(s->top==-1)//栈为空的情况
return false；
e=s->data[s->top];
return true;
}
1.1.2链栈
链栈的结构
链栈：采用链表存储的栈称为链栈（这里采用带头结点的单链表实现）
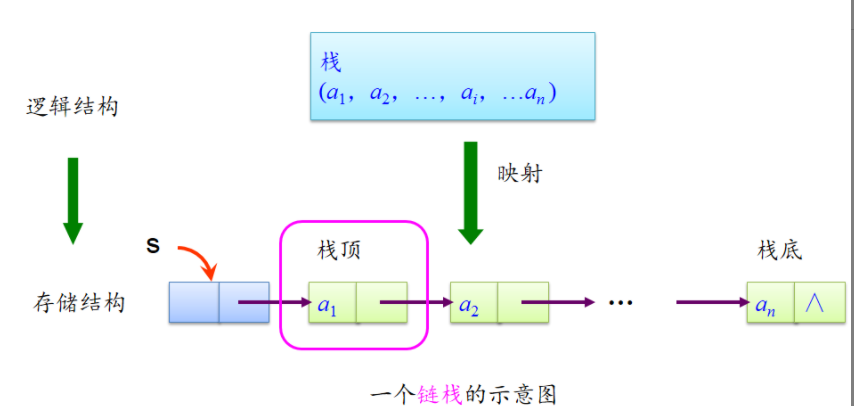
链栈中数据节点的类型LiStack定义如下：
typedef int ElemType;
typedef struct linknode
{ ElemType data;//数据域
struct linknode *next；//指针域
}LiNode，*LiStack；
- 链栈的四要素：
1.栈空条件：s->next=NULL
2.栈满条件：不考虑
3.进栈e操作：结点插入到头结点后，链表头插法
4.退栈操作：取出头结点之后结点的元素并删除之。
链栈的操作函数
1）初始化栈initStack（&s）
void initStack（LiStack &s）
{ s=new LiNode;
s->next=NULL;
}
2)销毁栈ClearStack（&s）
释放栈s占用的全部存储空间。同链表删除：
void DestroyStack（LiStack &s）
{ LiStack node；
while（s！=NULL）
{ node=s；
s=s->next；
delete node；
}
}
3）判断栈是否为空StackEmpty（s）
栈S为空的条件是s->next==NULL，同空链表
bool StackEmpty（LiStack s）
{
return（s->next==NULL）；
}
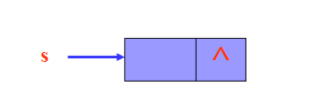
4）进栈Push（&s，e）
将新数据节点插入到头结点后
void Push(LiStack &S)
{ LiStack p;
p=new LiNode;
p->data=e;
p->next=s->next;//插入*p节点作为开始节点
s->next=p；
}//链栈不要考虑栈满情况！！！
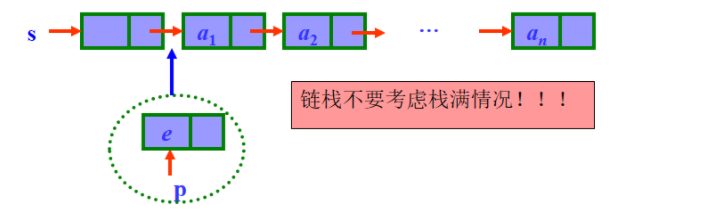
5）出栈Pop（&s，&e）
在栈不为空的条件下，将头结点后继数节点的数据域赋给e？？？？？
bool Pop(LiStack &s,ElemType &e)
{ LiStack p;
if (s->next==NULL)//栈空的情况
return false；
p=s->next；//p指向开始节点
e=p->data;
s->next=p->next;//删除*p节点
delete p； //释放*p节点
return true;
}//链栈，数据物理删除
6）取栈顶元素GetTop（s，e）
在栈不为空的条件下，将头结点后继数据节点的数据域赋给e。
bool GetTop(LiStack s,ElemType &e)
{ if(s->next==NULL)
return false；
e=s->next->data;
return true;
}
1.2 栈的应用
- C++模板类：stack
#include<stack>
1.stack<int> s:初始化栈，参数表示元素类型
2.s.push(t):入栈元素t
3.s.top():返回栈顶元素
4.s.pop():出栈操作只是删除栈顶元素，并不返回该元素。(物理删除，数据在栈内不存在。)
5.s1.empty():当栈空时，返回true。
6.s1.size():返问栈中的元素个数。
表达式求值
中缀表达式：运算符号位于两个运算数之间。如，a+bc-d/e*
后缀表达式(也叫逆波兰表达式)：运算符号位于两个运算数之后。如，abc+de/-*
1.中缀转后缀表达式：
- 要点：
1.优先级比栈顶运算符高入栈；
2.低或相等，一直出栈到栈顶为空或者更高，写入后缀表达式。 - 规则：
中缀表达式a + bc + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f + g * +。
转换过程需要用到栈，具体转换过程如下：
1）如果遇到操作数，就直接将其输出。
2）如果遇到操作符，则将其放入到栈中，遇到左括号时也将其放入栈中。
3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。
4）如果遇到任何其他的操作符，如（“+”， “”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下才弹出" ( "，其他情况都不会弹出" ( "。
5）如果读到了输入的末尾，则将栈中所有元素依次弹出。 - 实例：
输入为：a + b * c + (d * e + f)*g
处理过程：
1）首先读到a，直接输出。
2）读到“+”，将其放入到栈中。
3）读到b，直接输出。
此时栈和输出的情况如下：
4）读到“”，因为栈顶元素"+"优先级比" * " 低，所以将" * "直接压入栈中。*
5）读到c，直接输出。
此时栈和输出情况如下：
6）读到" + "，因为栈顶元素" * "的优先级比它高，所以弹出" * "并输出， 同理，栈中下一个元素" + "优先级与读到的操作符" + "一样，所以也要弹出并输出。然后再将读到的" + "压入栈中。
此时栈和输出情况如下：
7）下一个读到的为"("，它优先级最高，所以直接放入到栈中。
8）读到d，将其直接输出。
此时栈和输出情况如下：
9）读到" * "，由于只有遇到" ) "的时候左括号"("才会弹出，所以" * "直接压入栈中。
10）读到e，直接输出。
此时栈和输出情况如下：
11）读到" + "，弹出" * "并输出，然后将"+"压入栈中。
12）读到f，直接输出。
此时栈和输出情况：
13）接下来读到“）”，则直接将栈中元素弹出并输出直到遇到"("为止。这里右括号前只有一个操作符"+"被弹出并输出。
此时栈和输出情况：
14）读到" * "，压入栈中。读到g，直接输出。
15）此时输入数据已经读到末尾，栈中还有两个操作符“”和" + "，直接弹出并输出。*
2.后缀表达式求值：
注意点：借助栈存放操作数，进行操作的数为离运算符最近的2个数。
其求值过程可以用到栈来辅助存储。假定待求值的后缀表达式为6 5 2 3 + 8 * + 3 + ，其求值过程如下：
1）遍历表达式，遇到的数字首先放入栈中，此时栈如下所示：
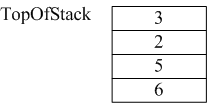
2）接着读到“+”，则弹出3和2，执行3+2，计算结果等于5，并将5压入到栈中。
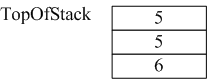
3）读到8，将其直接放入栈中。
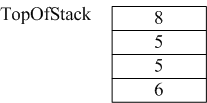
4）读到“”，弹出8和5，执行8*5，并将结果40压入栈中。而后过程类似，读到“+”，将40和5弹出，将40+5的结果45压入栈...以此类推。最后求的值288。
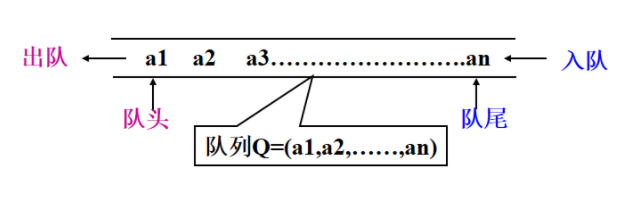
1.3 队列
- 队列的基本运算
①InitQueue（&q）：初始化队列。构造一个空队列q。
②DestroyQueue（&q）：销毁队列。释放队列q占用额存储空间。
③QueueEmpty（q）：判断队列是否为空。若队列q为空，则返回真；否则返回假。
④enQueue（&q，e）：进队列。将元素e进队作为队尾元素。
⑤deQueue（&q，&e）：出队列。从队列q中出队一个元素，并将其赋给e。
1.3.1顺序队列的结构
- 顺序队类型SqQueue定义：
typedef struct
{
Elem Type data[MaxSize];
int front,rear;//队首和队尾指针
}Queue;
typedef Queue*SqQueue;
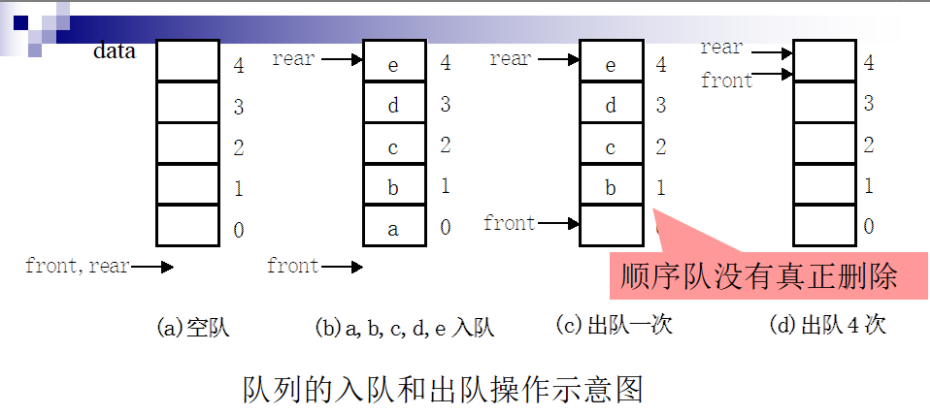
- 顺序队的四要素（初始时front=rear=-1）：
rear指向队尾元素；front指向队头元素的前一个位置
①队空条件：front=rear
②队满条件：rear=MaxSize-1
③元素e进队：rear++；data[rear]=e;
④元素e出队：front++；e=data[front];
1.3.2顺序队列的操作函数
（1）初始化队列InitQueue（q）
构造一个空队列q。将front和rear指针均设置成初始状态即-1值。
void InitQueue（SqQueue &q）
{
q=new Queue;
q->front=q->rear=-1;
}
(2)销毁队列DestroyQueue（q）
释放队列q占用的存储空间。
void DestroyQueue（SqQueue &q）
{
delete q;
}
(3)判断队列是否为空QueueEmpty（q）
若队列q满足q->front==q->rear条件，则返回true；否则返回false。
bool QueueEmpty(SqQueue q)
{
return (q->front==q->rear);
}
(4)进队列enQueue（q，e）
在队列不满的条件下，先将队尾指针rear循环增1，然后将元素添加到该位置。
bool enQueue(SqQueue &q,ElemType e)
{
if(q->rear+1==MaxSize) return false;//队满上溢出
q->rear=q->rear+1;
q->data[q->rear]=e;
return true;
}
(5)出队列deQueue（q,e）
在队列q不为空的条件下，将队首指针front循环增1，并将该位置的元素值赋给e。
bool de1Queue(SqQueue &q,ElemType &e)
{
if(q->front==q->rear) return false;//队空下溢出
q->front=q->front+1;
e=q->data[q->front];
return true;
}
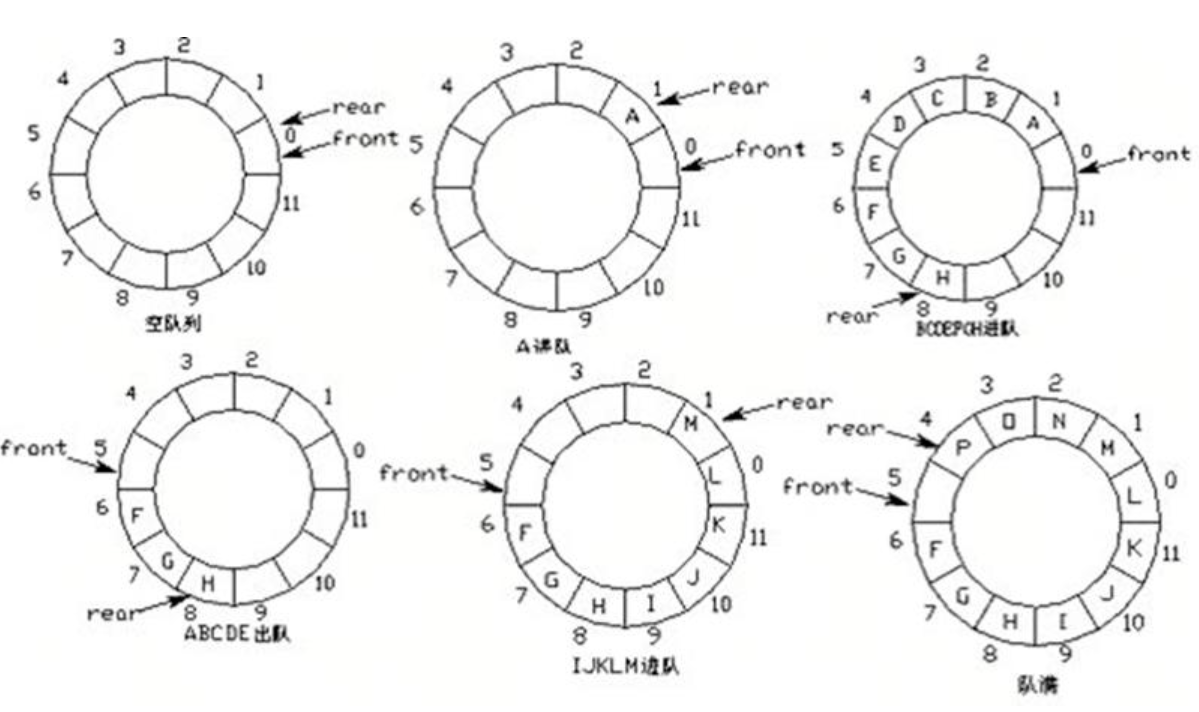
1.3.3环形队列（循环队列）的结构
结构体：
typedef struct
{
ElemType data[MaxSize];
int front,rear;
}Queue;
typedef Queue *SqQueue;
1.3.4环形队列的操作函数
①初始化队列：front=rear=0
②入队操作：rear=(rear+1)%MaxSize,data[rear]=e
③队满条件：（rear+1）%MaxSize=front
④出队操作：front=(front+1)%MaxSize,data[front]=e
⑤队空条件：front=rear
1)初始化队列
void InitQueue(SqQueue &q)
{ q=new Queue;
q->front=q->rear=0;
}
2)销毁队列：
void DestroyQueue(SqQueue &q)
{
delete q;
}
3）判断队列是否为空：
bool QueueEmpty(SqQueue q)
{
return (q->front==q->rear);
}
4)进环形队列
bool enQueue(SqQueue &q,ElemType e)
{ if((q->rear+1)%MaxSize==q->front)//队满上溢出
return false；
q->rear=(q->rear+1)%MaxSize;
q->data[q->rear]=e;
return true;
}
5)出环形队列：
bool deQueue(SqQueue &q,ElemType &e)
{ if(q->front==q->rear)//队空下溢出
return false;
e=q->data[q->front];
q->front=(q->front+1)%MaxSize;
return true;
}
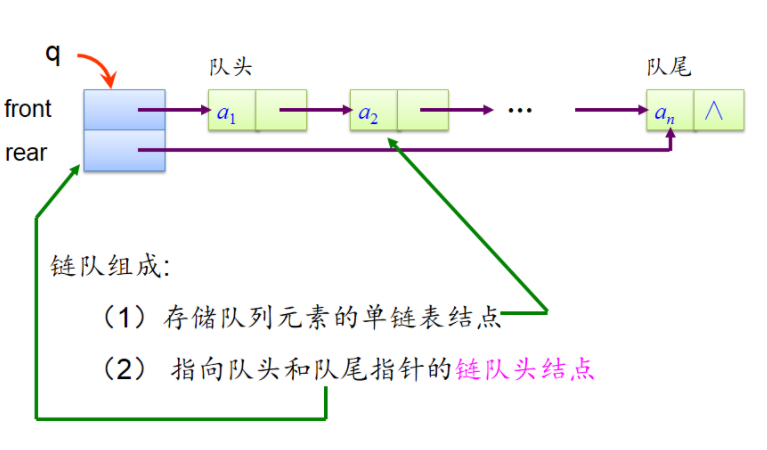
1.3.5链队列的结构
- 链队列结构体
单链表中数据节点类型QNode定义如下：
typedef struct qnode
{ ElenType data;//数据元素
struct qnode *next;
}QNode;
队列中头尾指针类型LinkQueue定义如下：
typedef struct
{ QNode *front;
QNode *rear;
}LinkQueue;//链队类型定义
- 链队的4要素：
1）队空条件：front=rear=NULL;
2)队满条件：不考虑
3）进队e操作：将包含e的节点插入到单链表表尾
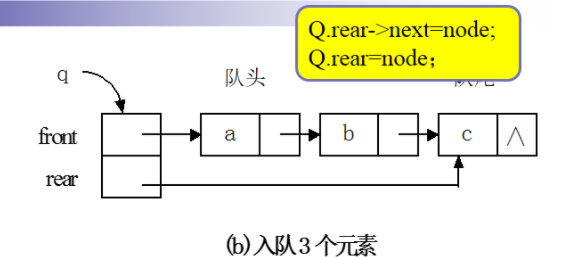
4）出队操作：删除单链表首数据节点
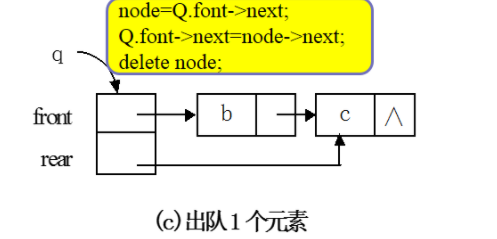
1.3.6链队列的操作函数
①链队列初始化
Status InitQueue(LinkQueue &Q)
{
Q.front=Q.rear=new QNode;
if(!Q.front)
exit(OVERFLOW);
Q.front->next=NULL;
return OK;
}
②判断队列是否为空
Status QueueEmpty(LinkQueue Q)
{
return (Q.front==Q.rear);
}
③求链队列的队头元素
Status GetHead(LinkQueue Q,QElemTypeType &e)
{
if(Q.front==Q.rear)
return ERROR;
e=Q.front->next->data;
return OK;
}
④链队列入队
Status EnQueue(LinkQueue &Q,QElemType e)
{
p=new QNode;
if(!p)
exit(OVERFLOW);
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
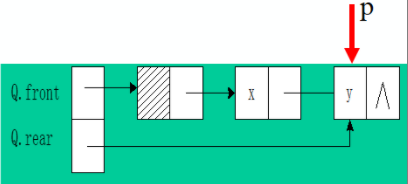
⑤链队列出队
Status DeQueue(LinkQueue &Q,QElemType &e)
{
if(Q.front==Q.rear)return ERROR;//队空，不操作
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.rear==p)Q.rear=Q.front;//最后一个元素被删，改队尾
delete p;
return OK;
}
1.3.7队列应用，要有具体代码操作。
C++语法，模板类：queue
#include<queue>
①q1.push(x):将元素x输入队列的末端
②q1.pop（）：弹出队列的第一个元素，注意：并不会返回被弹出元素的值。数据物理删除。（先取队头再pop）
③q1.front（）：取队头元素。
④q1.back（）：取队尾元素。
⑤q1.empty（）：当队列空时，返回true。
⑥q1.size（）：访问队列中的元素个数
eg.报数问题
- 解题思路：
1.调用头文件#include <queue>
2.需要判断当n<=m的情况，若n<=m则输出error！
3.双层循环。当报的数还没到m时，先保存，然后再弹出队列，接着再重新存入；当报的数等于m时，先保存此数，再弹出（即物理删除），最后输出。 - 伪代码：
int main()
{
int n,m,i,t;
if(n<=m) 输出error！
else
{
for(i=1;i<=n;i++)q.push(i);//输入元素
for(i=1;i<n;i++)
{
for(j=1;j<m;j++)
{
保存；
弹出；
重新进入队列；
}
用t保存当前数据；
弹出；
输出t；
}
输出队列最后一个头元素
}
}
- 具体代码：
#include <iostream>;
#include<queue>;
using namespace std;
queue<int>q;
int main()
{
int n, m, i;
int t;
cin >> n;
cin >> m;
if (n <= m)
{
cout << "error!" << endl;
}
else
{
for (i = 1; i <= n; i++)
{
q.push(i);//将元素i输入队列的末端
}
for (i = 1; i < n; i++)
{
for (int j = 1; j < m; j++)
{
t = q.front();
q.pop();
q.push(t);
}
t = q.front();
q.pop();
cout << t << " ";
}
cout << q.front();
}
}
🔅2.PTA实验作业（4分）
2.1 符号配对
- 具体代码
#include<stdio.h>
#include<string.h>
#include<stack>
#include<iostream>
using namespace std;
stack<char>q;
int main()
{
char s[100];
cin >> s;
int i=0;
int len = strlen(s);
for(i=0;i<len;i++)
{
if (s[i] != '{' && s[i] != '[' && s[i] != '(' && s[i] != '}' && s[i] != ']' && s[i] != ')')
{
continue;
}
if (s[i] == '{' || s[i] == '[' || s[i] == '(')
{
q.push(s[i]);//入栈
}
else if (s[i] == '}' || s[i] == ']' || s[i] == ')')
{
if (q.empty())
{
break;
}
else
{
//if (s[i] == '}' && q.top() == '{' || s[i] == ']' && q.top() == '[' || s[i] == '）' && q.top() == '（')
q.pop();//删除栈顶元素
}
}
}
if(q.empty()&&i==len)
{
cout << "yes";
}
else if (q.empty())
{
cout << "no";
}
else
{
cout << q.top() << endl;
cout << "no";
}
}
2.1.1 解题思路及伪代码
- 解题思路
1.先将字符串存入定义的字符数组里，算出字符串的长度
2.判断输入的符号，若不为‘{’，‘}’，‘[’,']','(',')'其中一个,则继续往下读字符；若为左半边符号则入栈；若为右半边符号则还需判断（若此时栈为空，则结束循环；若不为空，则弹出栈顶元素）
3.最后，如果栈为空且长度达到字符串的长度则说明匹配，输出yes；若此时只是栈为空，则输出no；若不匹配则输出当前栈顶元素再换行输出no。 - 伪代码
#include<stack>
int main()
{
char s[100];
int i=0;
int len=strlen(s);
for(i=0;i<len;i++)
{
if(不为左右符号的任何一个)
continue;//继续遍历
if(为左符号)
入栈；
else if(为右符号)
if(栈此时为空)
break；
else
弹出栈顶元素；
}
if(栈为空切且i=len)//即匹配成功
输出yes;
else if(栈为空)
输出no;
else(不匹配)
{
输出栈顶元素；
输出no；
}
}
2.1.2 总结解题所用的知识点
①栈的模板#include<stack>的应用
②运用栈进行存储符号并进行符号配对的判断
③扫描遍历字符串
2.2 银行业务队列简单模拟
2.2.1 解题思路及伪代码
- 解题思路
新建两个队列，定义flag=1，判断x的奇偶性，若为奇数则存入队列a，若为偶数则存入队列b。
当队列a和队列b均不为空时，先利用flag=1输出首个数据（空格问题），然后flag=0；如果a不为空，继续输出队列a中的一个数据，接着输出队列b的一个数据。
若队列a不为空队列b为空，则直接输出队列a的元素；
若队列b不为空队列a为空，则直接输出队列b的元素。 - 伪代码
定义两个队列a，b；
int main()
{
int n,x,t,flag=1;
输入n；
for(i=0;i<n;i++)
{
if(x为奇数)
存入队列a；
else(存入队列b)
}
while（队列a队列b均不为空）
{
if（flag为1）
{
输出队列a的头数据；
将flag置为1；
}
else
输出空格+队列a的头数据；
if（队列a不为空）
继续输出一个空格+队列a的头元素；
继续输出一个空格+队列b的头元素；
}
while（队列a不为空）
{
if（flag等于1）
{
输出队列a的队头元素
将flag置为0；
}
else
{
输出队列a的队头元素
}
弹出队列a的队头元素
}
while（队列b不为空）
{
if（flag等于1）
{
输出队列b的队头元素
将flag置为0；
}
else
{
输出队列b的队头元素
}
弹出队列b的队头元素
}
return 0；
}
2.2.2 总结解题所用的知识点
①运用队列模板queue#include<queue>
②数的奇偶性的判断
③进队列，出对列的操作
④运用flag进行空格的区别
🔅3.阅读代码（0--1分）
3.1 题目及解题代码
-
题目
-
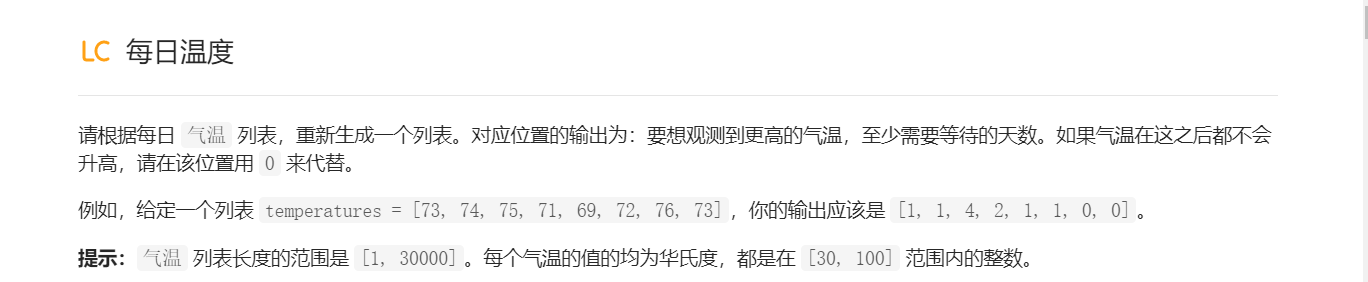
解题代码
public int[] dailyTemperatures(int[] T) {
Stack<Integer> stack = new Stack<>();
int[] ret = new int[T.length];
for (int i = 0; i < T.length; i++) {
while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
int idx = stack.pop();
ret[idx] = i - idx;
}
stack.push(i);
}
return ret;
}
作者：数据结构和算法
链接：https://leetcode-cn.com/leetbook/read/queue-stack/genw3/?discussion=OGBxRQ
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
3.2 该题的设计思路及伪代码
- 设计思路
1.在栈中存放数组元素的下标
2.将第一个数的下标0入栈
3.将后面的数和栈顶元素进行比较，若大于栈顶元素则弹出栈顶元素，接着继续比较该元素和新栈顶元素直到该元素比栈顶元素小或等于栈顶元素，就将该元素的下标入栈；若小于栈顶元素，则直接将该元素的下标入栈。
4.对应的天数即为遇到的第一个更大的数的下标减去自己的下标。 - 伪代码
public int[] dailyTemperatures(int[] T)
{
新建一个数组存放对应天数
for(int i=0;i<T.length;i++)
{
while(栈不为空且下一个数大于栈顶元素)
{
用idx记录此时栈顶元素的下标且弹出栈顶元素
求出栈顶元素需要等待的对应天数i-idx再将对应天数存入数组ret[idx]
}
将此时温度的对应下标入栈；
}
return ret;//返回所有数据对应的天数
}
时间复杂度：O（n2）：有两个循环，i<T.length,T[i] > T[stack.peek()]
空间复杂度：O（n）:需要将对应温度的数组下标存入栈int[] ret = new int[T.length]
3.3 分析该题目解题优势及难点。
- 解题优势
①代码符号简单明了，降低阅读难度；
②使用栈解题减少遍历次数，解题效率提高。
③利用栈只在一端进出与先进后出的特性，可以保存各个气温对应的下标，只需将当前元素下标减去栈顶元素下标即可计算出最近一次可观察到更高气温的天数。 - 难点
①不易想到应用栈来存放各数组元素的下标
②每个温度均需计算等待天数
③不易想到应用当前遇到的更高温度的下标减去栈顶元素的下标来计算的等待天数。
