通俗易懂的信息熵与信息增益（IE, Information Entropy; IG, Information Gain）

信息熵与信息增益（IE, Information Entropy; IG, Information Gain）

信息增益是机器学习中特征选择的关键指标，而学习信息增益前，需要先了解信息熵和条件熵这两个重要概念。

信息熵（信息量）

 

信息熵的意思就是一个变量i（就是这里的类别）可能的变化越多（只和值的种类多少以及发生概率有关，反而跟变量具体的取值没有任何关系），它携带的信息量就越大（因为是相加累计），这里就是类别变量i的信息熵越大。

系统越是有序，信息熵就越低；反之，一个系统越乱，信息熵就越高。所以，信息熵也可以说是系统有序化程度的一个衡量。

二分类问题中，当X的概率P(X)为0.5时，也就是表示变量的不确定性最大，此时的熵也达到最大值1。

条件熵

条件熵的直观理解：单独计算明天下雨的信息熵H(Y)是2，而条件熵H（Y|X）是0.01（即今天阴天这个条件下，明天下雨的概率很大，确定性很大，信息量就很少），这样相减后为1.99，在获得阴天这个信息后，下雨信息不确定性减少了1.99！是很多的！所以信息增益大！所以是否阴天这个特征信息X对明天下雨这个随机变量Y的来说是很重要的！

因为条件熵中X也是一个变量，意思是在一个变量X的条件下（变量X的每个值都会取），另一个变量Y熵对X的期望，这里的期望就是指所有情况各自概率的∑总和。

在文本分类中，特征词t的取值只有t（代表t出现）和（代表t不出现）。那么系统熵等于两种条件熵按比例求和：

 

示例说明条件熵

设样品房数据集样本12份，变量Y为房屋价格，根据价格计算该数据集的香农熵（即信息熵），其中价格高的4个占1/3，价格中等的6个占1/2，价格低的2个占1/6，其香农熵为：

 

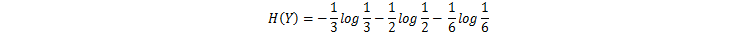
如图，在房屋的面积X这个条件下计算价格Y的条件熵，根据面积X，面积大的4个（价格3高1中）设为a，面积中的3个（价格3中）设为b，面积小的5个（价格1高2中2低）设为c，先分别计算a,b,c条件下的信息熵为：

再计算a,b,c信息熵的按比例求和，便得到在条件X条件下，Y的条件熵为：

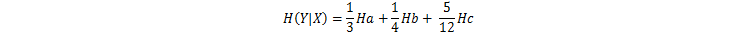
信息增益

评价一个系统的特征t对系统的影响程度就要用到条件熵，即是特征t存在和不存在的条件下，系统的类别变量i的信息熵。特征t条件下的信息熵与原始信息熵的差值就是这个特征给系统带来的信息增益。

信息增益最大的问题还在于它只能考察特征对整个系统的贡献，而不能具体到某个类别上，这就使得它只适合用来做所谓“全局”的特征选择（指所有的类都使用相同的特征集合），而无法做“本地”的特征选择（每个类别有自己的特征集合，因为有的词，对这个类别很有区分度，对另一个类别则无足轻重）。

 

附：特征提取步骤

1. 卡方检验

1.1  统计样本集中文档总数（N）。

1.2  统计每个词的正文档出现频率（A）、负文档出现频率（B）、正文档不出现频率（C）、负文档不出现频率（D）。

1.3 计算每个词的卡方值，公式如下：

1.4  将每个词按卡方值从大到小排序，选取前k个词作为特征，k即特征维数。

2. 信息增益

2.1  统计正负分类的文档数:N1、N2。

2.2  统计每个词的正文档出现频率（A）、负文档出现频率（B）、正文档不出现频率）、负文档不出现频率。

2.3  计算信息熵

2.4  计算每个词的信息增益

 

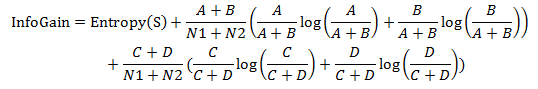
2.5  将每个词按信息增益值从大到小排序，选取前k个词作为特征，k即特征维数。