2020牛客多校第三场 E题Two Matchings（规律，dp）

2020牛客多校第三场 E题Two Matchings（规律，dp）

Two Matchings

题意：构造一个p数组，q数组，满足p[p[i]]=i，数组是1到n的排列，p，q数组每位都不同，答案为a数组每位与a[p[i]]的差的绝对值和a[q[i]]的差的绝对值的和。

题解：p数组很明显为a数组排序后将每相邻的两个相互连接；

问题是去找q数组，以下为几种找法；

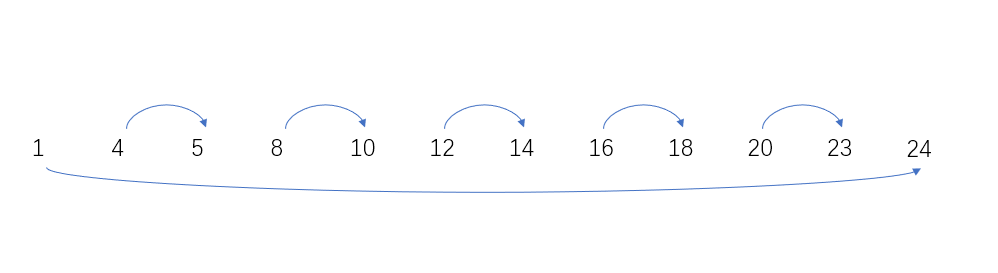
与前一个p合并：ans=(24-1) * 2;

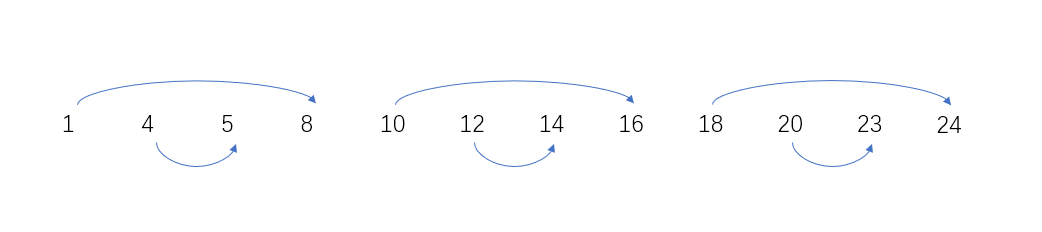
与前一个p合并：ans=(8-1) * 2+(16-10) * 2+(24-18) * 2;

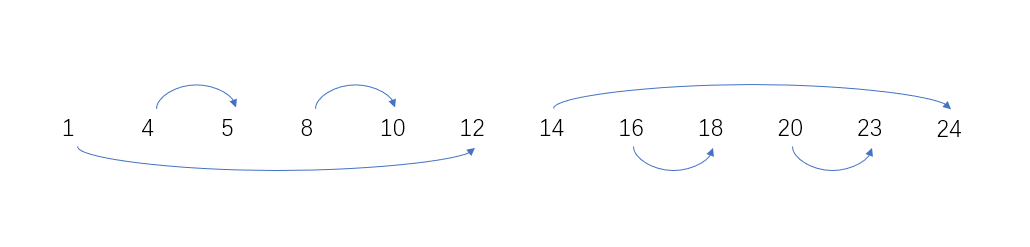
与前一个p合并：ans=(12-1) * 2+(24-14) * 2;

发现规律，ans的值会取决于q数组跨越的段数有关，且至少长度为4或6，段与段的间隔的值可以不记录答案，即答案为q跨越的区间的两倍，搜索其最短的跨越区间既可。

#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
const ll maxn=1e16+7;
ll t,n,a[200007],dp[200007];

ll dfs(ll p){
	if(p>=n){
		if(p==n){
			return 0;
		}
		else{
			return maxn;
		}
	}
	if(dp[p]!=-1){
		return dp[p];
	}
	return dp[p]=min(dfs(p+4)+a[p+3]-a[p],dfs(p+6)+a[p+5]-a[p]);
}

int main(){
	scanf("%lld",&t);
	while(t--){
		scanf("%lld",&n);
		for(int i=0;i<n;i++){
			scanf("%lld",&a[i]);
			dp[i]=-1;
		}
		dp[n]=-1;
		sort(a,a+n);
		printf("%lld\n",dfs(0)*2);
	}
}