AC自动机

AC自动机

模板题

AC自动机其实和kmp挺像的，主要是在优化时间方面，所以很多kmp题目也可以用ac自动机去写。

但这个题目用kmp写不了，因为kmp在一次比较中最多要花N+M的时间，而这个题目的特点是N很小但是多，kmp每次都要N+M的时间的话必然超时。

AC自动机的好处就在将所有要与m比较的字符串，合并成一棵树，跑一次M+sum（N），一次记录所有答案，而不是一次一次加。

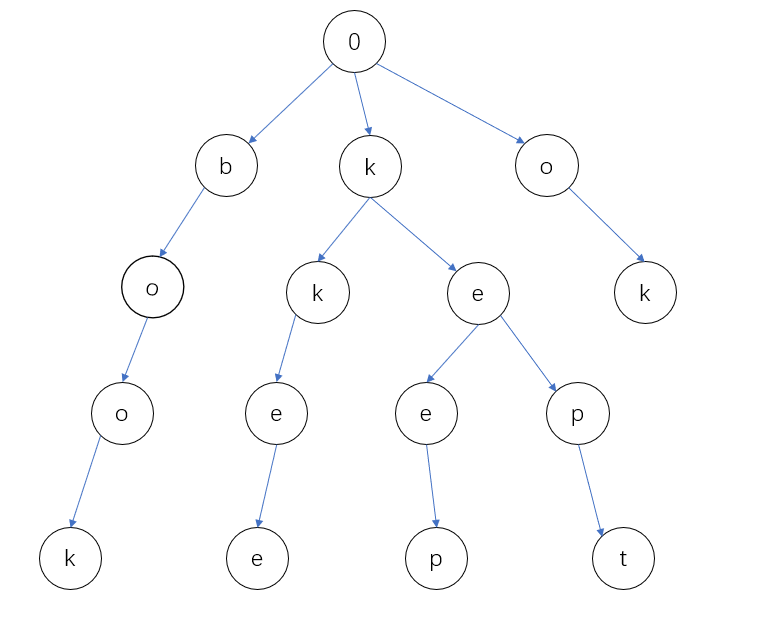
首先我举个栗子,来演示一下如何建树：book，kkee，ok，kept，keep；

红色表示子串的末尾，意思是当走到这个地方就说明包含这个子串

这里就给大家看个大概，具体请搜索字典树；

现在我们还需要一个fail数组这个是ac自动机的关键，我们搜bookkeeper，比如我们现在走完了book，但不只是包含了book，还包含了ok，所以我们下一步要走到ok的k字符处，然后我们走完k后，k也是kkee与kept的前缀，所以下一步我们要走到前缀k的位置，fail数组的作用就在这，这样跟着bookkeeper在树上跑一遍我们就能得到答案4。

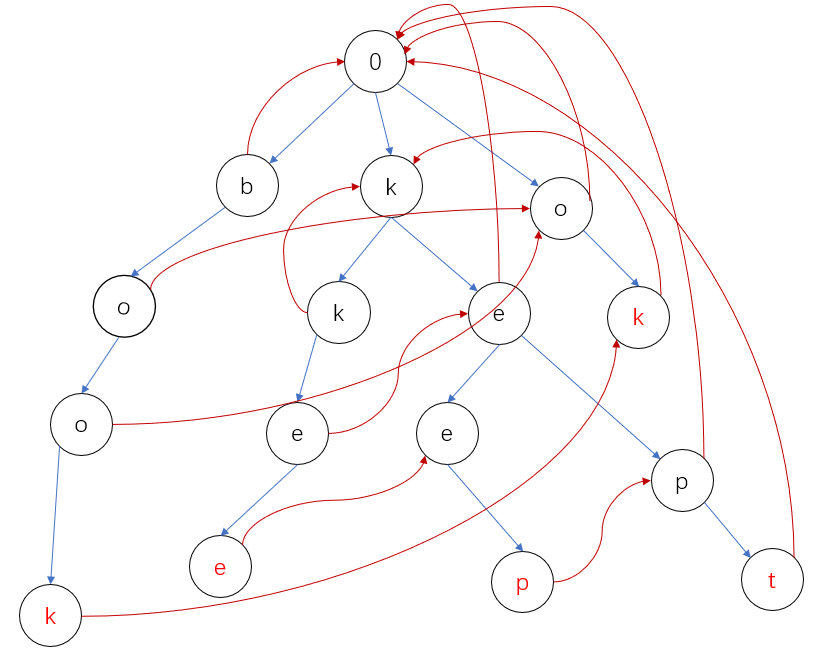
然后fail数组的构建方法就是该点父节点的fail到与该点字符相同的位置，若无则指向根节点，具体操作可看我模板，答案计算就是用m串遍历一遍既可。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int maxn=1e6+7;
int ma[maxn][26];
int fail[maxn];
int vis[maxn];
int t,n,cnt;
char s[maxn];
void init(){
	for(int i=0;i<=cnt;i++){
		for(int j=0;j<26;j++){
			ma[i][j]=0;
		}
		vis[i]=0;
		fail[i]=0;
	}
	cnt=0;
}
void build(string s){
	int now=0,len=s.length();
	for(int i=0;i<len;i++){
		if(ma[now][s[i]-'a']==0){
			ma[now][s[i]-'a']=++cnt;
		}
		now=ma[now][s[i]-'a'];
	}
	vis[now]++;
}
void fgo(){
	queue<int>sa;
	int lin,lin2;
	fail[0]=0;
	for(int i=0;i<=25;i++){
		if(ma[0][i]!=0){
			lin=ma[0][i];
			fail[lin]=0;
			sa.push(lin);
		}
	}
	while(!sa.empty()){
		lin=sa.front();
		sa.pop();
		for(int i=0;i<=25;i++){
			if(ma[lin][i]!=0){
				lin2=ma[lin][i];
				fail[lin2]=ma[fail[lin]][i];
				sa.push(lin2);
			}
			else{
				ma[lin][i] = ma[fail[lin]][i];
			}
		}
	}
}
int dfs(string s){
	int now=0,len=s.length(),sum=0;
	for(int i=0;i<len;i++){
		now=ma[now][s[i]-'a'];
		printf("now=%d\n",now);
		for(int j=now;j&&vis[j]!=-1;j=fail[j]){
            //printf("j=%d ",j);
			sum+=vis[j];
			vis[j]=-1;
		}
		puts("");
	}
	return sum;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=0;i<n;i++){
			scanf("%s",s);
			build(s);
		}
		fgo();
		scanf("%s",s);
		for(int i=1;i<=cnt;i++){
            printf("i=%d fail=%d\n",i,fail[i]);
		}
		printf("%d\n",dfs(s));
		init();
	}
}