2020牛客多校第二场 J题Just Shuffle(置换群与逆元)
2020牛客多校第二场 J题Just Shuffle(置换群与逆元)
题意:给一个排列(1,2,3,4,5...n),将它进行置换,x次置换后变成数组a,置换的意思是将第i位的元素替换到第j位,被替换的位置j必须与其他位替换,想当与要你定一个交换关系,之后每次置换都要按着交换关系来,x次时变成a数组。如果还有困惑可以学习一下我看到的一个大佬解释的置换群的基本定理:传送门
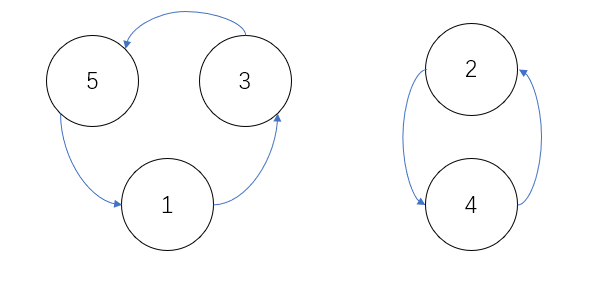
这个题想了一段时间的都估计能想到去找环,例如:5 4 1 2 3,你应该会发现,5和1换了,1和3换了,3和5换了,2和4换了,4和2换了,画出图应该是:
然后就是说,成环的肯定是要放一起考虑,因为很明显数字1必然可以经过1,3,5这3个位置,而且但它置换次数为其环大小时会变回原来的序列,我们不妨设某个环的大小为len,那么k必然是环原本的序列进行k%len次置换后的样子,然后就是你已知这个环k%len次置换的结果要你求一次置换的结果,枚举所有环,这是我比赛时的思路,但没学过置换群,我都不知道我用这些条件找不到置换一次的结果是什么,想假思路想了一下午,如图。
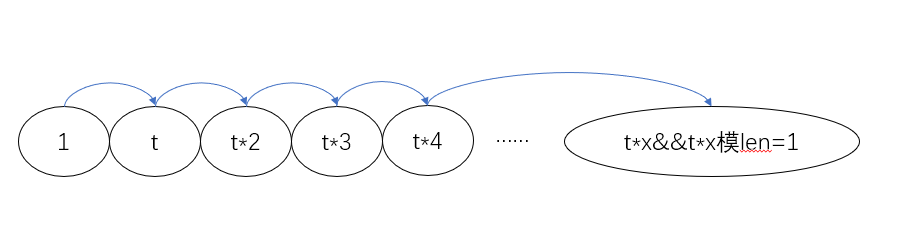
为什么找不到?因为我不知道转换关系,如果要枚举转换关系,那枚举量特别大到还要判断k次置换后是否等于a数组。看了一晚上题解弄懂后,发现还是自己太笨了。讲之前再强调一下,环再置换len次以后会变回原来的样子,转换k次等同于转化k%len次,我们让t=k%len,并且转换一次的答案等同于转换(?*len+1)次。现在我不一次一次的置换了,我一次就置换t次,那么a数组想当与我一次操作即置换t次后的结果,那么我进行x次操作,如果刚好,使其(x)乘(t)刚好等于某个(?)乘(len)+1不就是答案了吗(由于k的数据原因好像是不会出现找不到的情况,即不存在输出-1的可能)。列出公式即x * k % len=1,求出x既可,x * k % len = 1这个公式有没有很熟悉传送门。思路如图:
现在我们求出了逆元x(扩展gcd或者直接for暴力x(x<len)判断是否复合公式),要怎么构造答案,或者说怎么移动,如用b数组表示答案,c数组表示转换关系,b[c[i]]=c[(i+x)%len],把环看成有12个有数字的时针一个钟,如果动一次就是每个时针走一下,走x下就每个时针走x%len下,走12下回到原点,这个公式是置换群的整数幂运算公式,这边引用一个大佬的博客传送门
以下代码部分:
#include<iostream>
#include<vector>
#define ll long long
using namespace std;
int n,k,to[100007],vis[100007],ans[100007];
int a[100007];
vector<int>ho;
void dfs(int p){
vis[p]=1;
ho.push_back(a[p]);
if(vis[to[p]]==0){
dfs(to[p]);
}
}
void go(){
int len=ho.size(),inv;
for(int i=0;i<len;i++){
if((ll)i*k%len==1){
inv=i;
break;
}
}
for(int i=0;i<len;i++){
ans[ho[i]]=ho[(i+inv)%len];
}
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
to[i]=a[i];
}
for(int i=1;i<=n;i++){
ho.clear();
if(vis[i]==0){
dfs(i);
go();
}
}
for(int i=1;i<=n;i++){
printf("%d ",ans[i]);
}puts("");
}




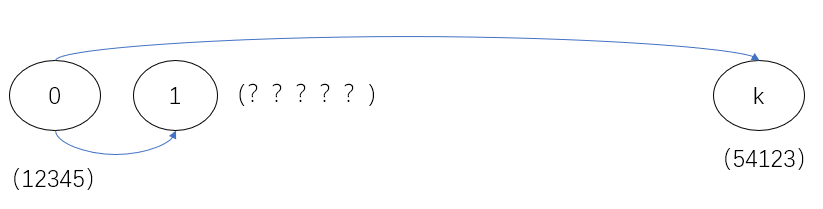


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!