【思维题】
【思维题】
找与解题有关的量
打表多造数据很关键!!!!!!!
观察一种东西的特殊性质
奇数 偶数(区域/总)
2的幂次
倍数 质数
最大值 最小值(序列)
取模
对称
一直+-*/再还原
左右最小/最大/最近/最远
头尾01
逆序对
多观察规律
多想性质
多用代码行数短的做法
注意分类讨论!!!
Scarecrow
跳格子问题
直接考虑最简单的情况:一跳到底
https://codeforces.com/contest/2055/problem/D
思路
第一个点必须在0
考虑两个点的情况
(1)若两个点距离小于k:不需要挪动可以直接跳
(2)若两个点距离大于k但小于k+当前挪动所花的时间:可以从一开始就挪到a[i-1]+k
(3)若两个点距离大于k+当前挪动所花的时间:a[i]从一开始就要挪动,并在到达a[i-1]时相向而行
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=200010;
int t;
int n,k,l;
//记得开长整型!
long double a[N];
long double ans,timenow;
void solve(){
cin>>n>>k>>l;
for(int i=1;i<=n;i++) cin>>a[i];
//初始化第一个点
ans=a[1]*2;
timenow=a[1];
a[1]=0;
for(int i=2;i<=n;i++){
if(a[i]-a[i-1]>k){
if(a[i]-a[i-1]>k+timenow){
a[i]-=timenow;//在一开始就要挪
ans+=(a[i]-a[i-1]-k);
timenow+=(a[i]-a[i-1]-k)/2;//相向而行 所以时间/2
a[i]-=(a[i]-a[i-1]-k)/2;
}
else{
a[i]=a[i-1]+k;
}
}
else{
a[i]=min(a[i-1]+k,a[i]+timenow);
}
}
//最后一个点到终点
ans+=max((l-a[n]-k)*2,(long double)0);
cout<<(ll)ans<<"\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--){
solve();
}
return 0;
}
翻之
https://ac.nowcoder.com/acm/contest/100671/C
代码
//把每一列存下来 一样的最多的就是答案(这些列能够同时变成1)
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=3010;
string a[N];
int n,m;
string s[N];
map<string,int> q;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=0;i<n;i++) cin>>s[i];
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[j]+=s[i][j];
}
}
for(int i=0;i<m;i++){
q[a[i]]++;
}
int ans=-1;
for(auto [key,value]:q){
ans=max(ans,value);
}
cout<<ans;
return 0;
}
mex和gcd的乘积
https://ac.nowcoder.com/acm/contest/66877/C
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=100010;
int n,a[N];
int t[N];
int gcd(int a,int b){
if(a==0) return b;
if(b==0) return a;
return b?gcd(b,a%b):a;
}
/*【本题需要分类讨论!!!】
当一个区间的
mex>1:一定包含1 那么最大值就是mex
mex==1:数组只有0和>1的数 那么我们就选0和0前后最大的一个数
mex==0:答案为0
->注意是一题区间问题:
答案即为mex和gcdmax的较大值(mex>=1时)
注意要特判 整个数组为0时答案就是0!!!
*/
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
t[a[i]]++;
}
int mex=0;
int ans=0;
while(t[mex]) mex++;
if(mex>=1){
int gcdmax=mex;
for(int i=1;i<=n;i++){
if(a[i]==0){
gcdmax=max(gcdmax,a[i-1]);
gcdmax=max(gcdmax,a[i+1]);
}
}
ans=gcdmax;
}
else if(mex==0) ans=0;
//要特判整个数组为0时 答案为0
if(t[0]==n) ans=0;
cout<<ans;
return 0;
}
Cost of the Array
https://codeforces.com/contest/2059/problem/B
考虑特殊情况下的特判
一般情况下的简单性
思路
当k==n时,答案唯一 -> 直接模拟
当k!=n时,答案只能从1和2中产生
->枚举每个第二个数组的首位:2~n-k+2
如果全为1->答案为2
否则答案为1
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=2e5+10;
int t;
int n,k;
int a[N];
void solve(){
cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i];
int ans=1;
if(n==k){
vector<int> q;
for(int i=2;i<=n;i+=2){
q.push_back(a[i]);
}
q.push_back(0);
for(int j=0;j<q.size();j++){
if(q[j]!=j+1){
ans=j+1;
break;
}
}
}
else{
//枚举第二个被划分数组起点:范围从2~n-k+2:如果只有1那答案为2
ans=2;
for(int i=2;i<=n-k+2;i++){
if(a[i]!=1){
ans=1;
break;
}
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--) solve();
return 0;
}
Tokitsukaze and Balance String (hard)
打表找规律->就可以发现问题没那么复杂
当没思路的时候就从最简单的情况造样例考虑
https://ac.nowcoder.com/acm/contest/95336/C
/*
打表找规律!!!
过的人多->规律题!
*/
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const ll mod=1e9+7;
int t;
int n;
string s;
/*
不要管问号 打表找规律
首尾相同的一定平衡
首位不同的一定不平衡
->平衡的就只需要变中间的就可
->分类讨论
*/
ll qmi(ll a,ll k,ll p){
ll res=1;
while(k){
if(k&1) res=res*a%p;
k>>=1;//删去k的末位
a=a*a%p;
}
return res;
}
void solve(){
cin>>n;
cin>>s;
ll ans=0;
if(n==1){
if(s[0]=='?') ans=2;
else ans=1;
}
else{
//统计?个数
int cnt=0;
for(int i=0;i<n;i++){
if(s[i]=='?') cnt++;
}
//首尾都是问号
if(s[0]=='?' && s[n-1]=='?'){
//为了平衡:都为0或者都为1
ll res=qmi(2,cnt-2,mod);
/*首尾四种情况:
1 1/0 0->只能变中间n-2
1 0/0 1->只能变两边随便一个->2
->(n-2+2)=n 有合并所以*2
*/
res=res*n%mod;
res=res*2%mod;
ans=res;
}
//首尾有1个是问号
else{
if(s[0]=='?'){
ll res=qmi(2,cnt-1,mod);
/*如果首和尾相同->变中间 +(n-2)
首和尾不同->变首或者变尾都行 +2
*/
res=res*n%mod;
ans=res;
}
else if(s[n-1]=='?'){
ll res=qmi(2,cnt-1,mod);
res=res*n%mod;
ans=res;
}
//首尾都不是问号
else{
ll res=qmi(2,cnt,mod);
if(s[0]!=s[n-1]){//首尾不同
//首尾必须变一个
res=res*2%mod;
}
else{//首尾相同:只能变中间
res=res*(n-2)%mod;
}
ans=res;
}
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--) solve();
return 0;
}
Customer Service
https://codeforces.com/contest/2059/problem/C
思路
观察样例:发现答案和后缀1的个数有关系
后缀1的个数表示最大能提供的数(而应当删连续后缀1前面的那个)
(注意是最大!!!小值也可以
数据:
1
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
->答案是4而不是5
)
->求后缀1,排序,然后不断累计答案(只要当前个数>=ans ans就能累加)
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
const int INF=0x3f3f3f3f;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=310;
int t;
int n;
int a[N][N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j];
vector<int> q;
for(int i=1;i<=n;i++){
int cnt=0;
for(int j=n;j>=1;j--){
if(a[i][j]==1) cnt++;
else break;
}
q.push_back(cnt);
}
//找最大连续后缀1的个数
sort(q.begin(),q.end());
int ans=0;
for(int i=0;i<n;i++){
if(q[i]>=ans) ans++;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--) solve();
return 0;
}
小L的位运算
https://ac.nowcoder.com/acm/contest/95337/C
【首先想到分类讨论】
【其次想到贪心】
思路
显然,已经满足条件的位置不需要再变更
->不满足条件的位置分4类:01 10 11 01
->类与类内部不能交换,类与类之间均可交换
结论
若众数<一半 排序后直接对半分
否则全部对齐众数
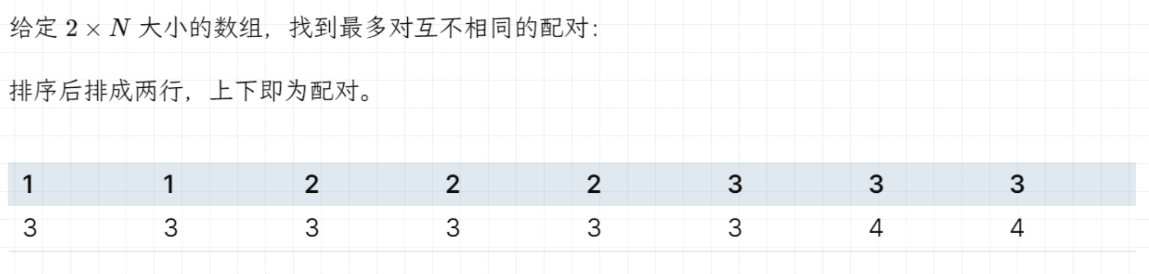
->若最大值超过一半->全部对齐交换
->否则均可交换->可能会剩一两个

代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
int n;
ll x,y;
string a,b,c;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>x>>y;
cin>>a>>b>>c;
/*
【思路】
统计答案和c对不上的 00 01 10 11个数
每个组之间都能对换->优先换大的,直到剩一个数
最后剩下的就只能反置了
*/
ll zz=0,zo=0,oz=0,oo=0;
for(int i=0;i<n;i++){
int ai=a[i]-'0';
int bi=b[i]-'0';
int ci=c[i]-'0';
if(ai^bi!=ci){
if(ai==0 && bi==0) zz++;
else if(ai==1 && bi==0) oz++;
else if(ai==0 && bi==1) zo++;
else if(ai==1 && bi==1) oo++;
}
}
ll ans=0;
/*
(1)如果最大的超过了一半 那么全部盯着最大的看(所有类型都不能内部消化 和最大的消化最好) 最大减完然后反置
(2)如果最大的没超过一半->内部会全部消化(结论) 最后剩下0或1个用来反置
*/
vector<ll> q;
ll sum=zz+oo+zo+oz;
q.push_back(zz);
q.push_back(oo);
q.push_back(zo);
q.push_back(oz);
sort(q.begin(),q.end());
ll mx=q[3];
if(mx>sum/2){
ans=(sum-mx)*y+(mx-(sum-mx))*x;
}
else{
ans=(sum/2)*y+(sum&1)*x;
}
if(x*2<y){
ans=x*sum;
}
cout<<ans;
return 0;
}
小紫的优势博弈
思路
※※※从后往前构建
在%2环境下 有4种状态
ze on
0 0->直接算结果
1 0
0 1
1 1
->发现后三种情况只会不能满足条件1次:奇数个0/奇数个1/1个0一个1
->判断情况 遇到解锁
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
int n;
string s;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
cin>>s;
s=' '+s;
vector<int> ze(n+2,0),on(n+2,0);
for(int i=n;i>=1;i--){
if(s[i]=='0'){
ze[i]=ze[i+1]+1;
on[i]=on[i+1];
}
else if(s[i]=='1'){
ze[i]=ze[i+1];
on[i]=on[i+1]+1;
}
}
int res=0;
int tag0=1,tag1=1,tag01=1;
for(int i=n;i>1;i--){
if(ze[i]%2==0 && on[i]%2==0) res++;
else if(ze[i]%2==1 && on[i]%2==0){
if(tag0) tag0=0;
else res++;
}
else if(ze[i]%2==0 && on[i]%2==1){
if(tag1) tag1=0;
else res++;
}
else if(ze[i]%2==1 && on[i]%2==1){
if(tag01) tag01=0;
else res++;
}
}
if(n<=2) res=0;
double ans=(double)res/(double)n;
cout<<fixed<<setprecision(7)<<ans<<endl;
return 0;
}
mex
https://ac.nowcoder.com/acm/contest/105825/D
思路
首先考虑无解/不用操作的情况:
(1)如果整个数组没有0->mex为0->怎么减都没办法减到相同->无解
(2)如果整个数组本来就是全相同->不需要操作->解为0
然后考虑扣mex的情况:
首先给数组排序
因为每个大的数都会依托于小的数扣
比如 0 1 2 5->5会被0 1 2产生的mex扣:扣去3
所以产生差分公式:a[i]-a[i-1]-1 记得mex比该数多1->再多减1->即为对答案的贡献

代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a<b;}
const int N=1e5+10;
int n;
ll a[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
int is_same=0;
bool is_zero=0;
for(int i=1;i<=n;i++){
cin>>a[i];
if(a[i]==0) is_zero=1;
if(a[i]==a[1]) is_same++;
}
if(is_same==n) cout<<0;
else if(!is_zero) cout<<-1;
else{
sort(a+1,a+1+n,cmpll);
ll ans=1;
for(int i=2;i<=n;i++) ans+=max_(0,a[i]-a[i-1]-1);//注意这里 如果对答案没贡献(比如两个数相同)那么贡献为0->注意区最大值
cout<<ans;
}
return 0;
}
小红开灯(三,hard)
https://ac.nowcoder.com/acm/contest/107000/D
一定要注意到本题k比n的关系大!!!
思路
(1)先考虑n和k的关系问题
①若k==n:只有全0和全1两种状态 -> 特判
②若k<n:改变k盏灯->改变任意2盏灯的状态
(2)打表 考虑结论:
①k是奇数:结合上面结论->我可以改变任何一盏灯的状态->2^n
②k是偶数:我只能改变偶数盏灯的状态
C(n,0)+C(n,2)+C(n,4)+...+C(n,2k)->2^(n-1)
代码
const ll mod=1e9+7;
ll n,k;
ll qmi(ll a,ll k,ll p){
ll res=1;
while(k){
if(k&1) res=res*a%p;
k>>=1;
a=a*a%p;
}
return res;
}
void solve(){
cin>>n>>k;
if(n==k) cout<<"2"<<endl;
else if(k<n){
if(k%2){
ll ans=qmi(2,n,mod);
cout<<ans<<endl;
}
else{
ll ans=qmi(2,n-1,mod);
cout<<ans<<endl;
}
}
}
Asuna and the Mosquitoes
https://codeforces.com/contest/2092/problem/C
别想太多!性质很简单 奇数化成1
int n;
/*
【结论题】
1.若只有奇数/偶数:最大
2.若同时拥有:答案为和-奇数个数+1
->选择一个偶数 构造偶数+(奇数-1)=偶数 奇数->1
->偶数可以完全吃掉一个奇数
->有多个偶数?最后只能留一个偶数吃掉变成奇数 其他最后都会变成奇数->化成1
*/
void solve(){
cin>>n;
vector<ll> a(n+1,0);
ll sum=0;
ll maxx=0,jicnt=0,oucnt=0;
for(int i=1;i<=n;i++){
cin>>a[i];
sum+=a[i];
maxx=max_(a[i],maxx);
if(a[i]%2) jicnt++;
else oucnt++;
}
if(jicnt==0 || oucnt==0){
cout<<maxx<<endl;
}
else{
cout<<(sum-jicnt+1LL)<<endl;
}
}
操作字符串
https://ac.nowcoder.com/acm/contest/107879/D
注意“最小公倍字符串”和最大公约数的关系
字母只有26个 考虑O(26*N)
int b[N][27];
void solve(){
cin>>n;
int len=0;
for(int i=1;i<=n;i++){
cin>>a[i];
int l=a[i].size();
if(i==1) len=l;
else len=gcd(len,l);
}
//cout<<len<<endl;
for(int i=1;i<=n;i++){
int l=a[i].size();
for(int j=0;j<l;j++){
int tt=a[i][j]-'a';
b[j%len][tt]++;
}
}
for(int i=0;i<len;i++){
sort(b[i],b[i]+26,cmp);
/*
for(int j=0;j<26;j++){
cout<<b[i][j]<<" ";
}
cout<<endl;
*/
}
int ans=0;
for(int i=0;i<len;i++){
for(int j=1;j<26;j++){
ans+=b[i][j];
}
}
cout<<ans<<endl;
}
至
https://ac.nowcoder.com/acm/contest/109904/C
先想到一些显然的结论 然后写下来造数据->能找到规律
int n;
int a1,b1,a2,b2;
/*
【结论题分类讨论】
后面必须追上 前面必须被阻挡:已知每次阻挡+1格 只有在前面的可以阻挡:只能被挡1次
(1)两点相同位置
(2)A 0 : 可以在B的路线上挡一格 使得B多加1格
0 B
(3)0 B : B本来就需要下来1格
A 0
※注意B不能是终点或者终点前1列
->总结
(1)两点相同一定YES
(2)两点不同:①在前面的点只能在后面的点1格
②在前面的点不能在n和n-1列?
0 B
A 0
这种可以:因为不需要障碍
A 0
0 B
这种不可以:因为需要障碍
*/
void solve(){
//A永远在上面 B永远在下面
cin>>n;
cin>>a1>>b1>>a2>>b2;
if(a1==a2 && b1==b2){
cout<<"YES"<<endl;
return;
}
if(b1>b2){//小的点在前面 大的点在后面
swap(a1,a2);
swap(b1,b2);
}
if(b1+1==b2){//在前面的点只能在后面的点前1格
if(a1==a2+1){
cout<<"YES"<<endl;
return;
}
if(a1+1==a2 && b2<n-1){//在前面的点不能是n和n-1 a的+1-1关系随便
cout<<"YES"<<endl;
return;
}
}
cout<<"NO"<<endl;
}
小宇
https://ac.nowcoder.com/acm/contest/112544/E
思路

代码
int n;
void solve(){
cin>>n;
vector<int> a(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
map<int,int> cnt;
for(int i=1;i<=n;i++){
cnt[a[i]]++;
}
int r=n;
while(r>0 && (r==n || a[r]<a[r+1]) && a[r]>=r && cnt[a[r]]==1){
r--;
}
set<int> q;
for(int i=1;i<=r;i++){
if(a[i]!=i) q.insert(a[i]);
}
int ans=q.size();
cout<<ans<<endl;
}
Good Start
分类讨论多造数据写情况->合成结论
https://codeforces.com/contest/2113/problem/B
题目大意

思路:分类讨论
把h和w轴分开讨论
(1)有一个轴相距的距离接近重合 (差值<=0)
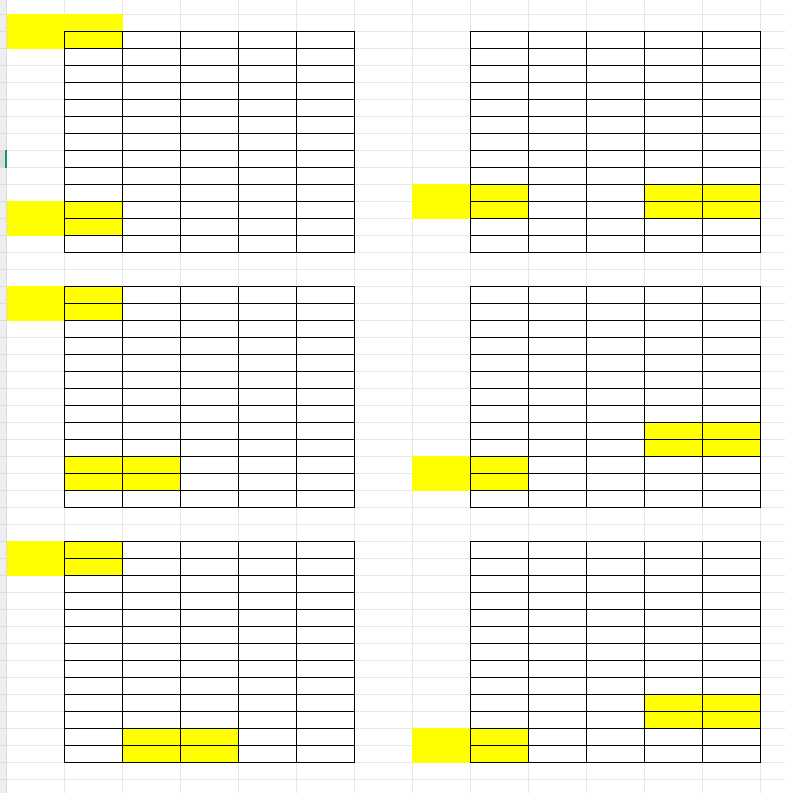
->此时没重合的轴必须要满足对应的能正好铺满:len%a(b)==0
(2)考虑大小?hd<a wd<b?
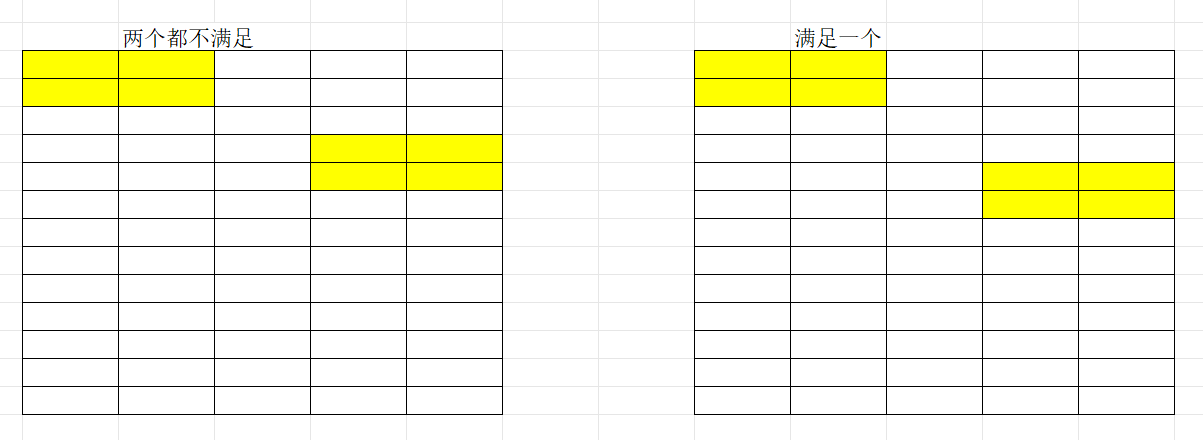
如果都小于肯定不满足
有一个大于可能能满足
->结合(1)(2)发现要讨论取模!
【结论】
->若两个都没办法整除:铺不完
->有一个可以整除:可以铺完->另一个轴可以补一个让他满足条件
代码
int w,h,a,b;
int x[2],y[2];
void solve(){
cin>>w>>h>>a>>b;
cin>>x[0]>>y[0]>>x[1]>>y[1];
int wd=0,hd=0;
if(x[0]<x[1]){
wd=x[1]-(x[0]+a);
}
else{
wd=x[0]-(x[1]+a);
}
if(wd<0) wd=-1;
if(y[0]<y[1]){
hd=y[1]-(y[0]+b);
}
else{
hd=y[0]-(y[1]+b);
}
if(hd<0) hd=-1;
if(hd==0 || wd==0){
cout<<"Yes"<<endl;
return;
}
if(hd<0){
if(wd%a) cout<<"No"<<endl;
else cout<<"Yes"<<endl;
return;
}
if(wd<0){
if(hd%b) cout<<"No"<<endl;
else cout<<"Yes"<<endl;
return;
}
if(wd%a==0 || hd%b==0) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
Leftmost Below
https://codeforces.com/contest/2128/problem/C
题目大意
构造一个数组a,问其能不能变成b
每次可以选一个位置i和一个x,要求满足a[i]<x且a[1~i-1]>=x,此时可给a[i]+=x
结论
【方法】
(1)多造一些n=3的样例
(2)想一下一个数如何*从0变成b[i]*
对于b[i],设min=(b[1],...b[i-1])
若b[i]-min<min,则说明是可构造的
->构造方式:
若b[i]
若b[i]>=min->先加b[i]-min,再加min->这里可以看出b[i]-min一定要比前面大 不然加不上
代码
int n;
void solve(){
cin>>n;
vector<int> b(n+1,0);
for(int i=1;i<=n;i++) cin>>b[i];
int minn=inf_int;
for(int i=1;i<=n;i++){
if(b[i]-minn>=minn){
cout<<"NO"<<endl;
return;
}
minn=min(minn,b[i]);
}
cout<<"YES"<<endl;
}
Make it Equal
https://codeforces.com/contest/2131/problem/C
题目大意

思路
涉及+k/-k -> 考虑模k的情况下会怎么样!!!
代码
const int N=3e5+10;
int n;
i64 k;
void solve(){
cin>>n>>k;
vector<i64> s(n+1,0),t(n+1,0);
for(int i=1;i<=n;i++) cin>>s[i];
for(int i=1;i<=n;i++) cin>>t[i];
for(int i=1;i<=n;i++){
s[i]=min64(s[i]%k,(k-s[i]%k)%k);
t[i]=min64(t[i]%k,(k-t[i]%k)%k);
}
sort(s.begin()+1,s.end(),cmp64);
sort(t.begin()+1,t.end(),cmp64);
if(s==t) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
XNOR Operation
https://atcoder.jp/contests/abc418/tasks/abc418_d
题目大意

思路
本题和总奇偶有关
【观察】
01->0 10->0 --> 1个0
11->1 00->1 --> 偶数个0
->一个子串只要有偶数个0最后就会变成1->前缀和统计即可
代码
int n;
string s;
void solve(){
cin>>n>>s;
i64 cnt[2]{1LL,0};
i64 sum=0;
i64 ans=0;
for(int i=0;i<n;i++){
int t=s[i]-'0';
sum+=(t==0);
ans+=cnt[sum&1];
cnt[sum&1]++;
}
cout<<ans<<endl;
}
Niko's Tactical Cards
https://codeforces.com/contest/2173/problem/B
题目大意
n个回合,每个回合可以选择\(a_i\)和\(b_i\)
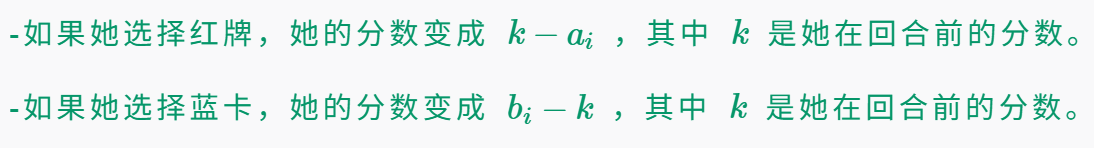
找n个回合后的最大k
思路
贪心思路失效:每个回合的最大值不一定就是最后结果的最大值
->同时考虑最大值和最小值:
最后答案就是\(max_n\)。
代码
int n;
void solve(){
cin>>n;
//int k=0;
vector<i64> a(n+1,0),b(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
i64 mx=0,mn=0;
for(int i=1;i<=n;i++){
i64 nmx=mx,nmn=mn;
mx=whink_max<i64>(nmx-a[i],b[i]-nmn);
mn=whink_min<i64>(nmn-a[i],b[i]-nmx);
}
cout<<mx<<endl;
Kanade's Perfect Multiples
https://codeforces.com/contest/2173/problem/C
题目大意
给定序列a,其中每个数不大于k
要求构造一个元素最少的序列B,使得:
(1)B序列内的数必须是\(a_i\)的某一因数
(2)\(b_i\)的每一个\(<=k\)的倍数必须在\(a_i\)出现
构造数组,若无输出-1
思路
暴力做法:把所有数的所有因数找出来然后遍历
->观察条件:\(b_i\)的每一个\(<=k\)的倍数必须在\(a_i\)出现
->那么最小的数也必然在\(a_i\)出现
->排序,从最小的数开始找即可
代码
int n;
i64 k;
void solve(){
cin>>n>>k;
vector<i64> a(n+1,0);
map<i64,bool> exi;
for(int i=1;i<=n;i++){
cin>>a[i];
exi[a[i]]=1;
}
sort(a.begin()+1,a.end(),cmp<i64>);
map<i64,bool> st;
vector<i64> ans;
for(int i=1;i<=n;i++){
if(st[a[i]]) continue;
bool is_ok=true;
for(i64 j=a[i];j<=k;j+=a[i]){
if(!exi[j]){
is_ok=false;
break;
}
}
if(is_ok){
ans.push_back(a[i]);
for(i64 j=a[i];j<=k;j+=a[i]){
st[j]=1;
}
}
}
/*
for(auto [key,val]:st){
cout<<key<<" "<<val<<endl;
}
*/
for(int i=1;i<=n;i++){
if(!st[a[i]]){
cout<<-1<<endl;
return;
}
}
cout<<ans.size()<<endl;
for(auto son:ans){
cout<<son<<" ";
}
cout<<endl;
}
Blackslex and Girls
判断
YES或NO的题目:如果有很明显的偏向一边->找条件
https://codeforces.com/contest/2179/problem/E
题目大意

代码
int n;
i64 x,y;
string s;
//模拟即可
void solve(){
cin>>n;
cin>>x>>y;
cin>>s;
s=' '+s;
vector<i64> p(n+1,0);
for(int i=1;i<=n;i++) cin>>p[i];
//条件1
i64 sump=0;
for(int i=1;i<=n;i++){
sump+=p[i];
}
if(sump>(x+y)){
cout<<"NO"<<endl;
return;
}
/*条件2
因为a[i]+b[i]>=p[i],且a[i]和b[i]有严格的大小关系
那么较大的那个最少要为p[i]/2+1 那么较小的p[i]/2是可以拿来【动态分配】的
->算较大最小值加起来看看是否超过限制
*/
i64 lima=0,limb=0;//限制
i64 rema=0,remb=0;//动态分配
for(int i=1;i<=n;i++){
if(s[i]=='0'){
lima+=(p[i]/2LL+1LL);
remb+=(p[i]/2LL);
}
else if(s[i]=='1'){
limb+=(p[i]/2LL+1LL);
rema+=(p[i]/2LL);
}
}
if(lima>x || limb>y){
cout<<"NO"<<endl;
return;
}
/*条件3:特判
若二进制串全为0或1:较大的那个数组总和-n 不能小于 较小的
eg:n=3 x=5 y=3 p=[1,1,1]
a 2 2 1
b 1 1 1
无法满足
*/
int ext0=0,ext1=0;
for(int i=1;i<=n;i++){
if(s[i]=='0') ext0++;
else if(s[i]=='1') ext1++;
}
if(ext0==n){
if((x-n)<y){
cout<<"NO"<<endl;
return;
}
}
else if(ext1==n){
if((y-n)<x){
cout<<"NO"<<endl;
return;
}
}
cout<<"YES"<<endl;
}
Production of Snowmen
https://codeforces.com/contest/2182/problem/C
找性质 优化一维+暴力循环判断答案
\(O(n^4)->O(n^2)\)
题目大意

思路
(1)三维->两维:偏移量(x,y)
a数组从p开始
b数组相对于a数组偏移x
c数组相对于b数组偏移y,即c数组相对于b数组
(2)注意到他要整个序列都满足:只要偏移量(x,y)是对的,那么对于1<=p<=n来说全部满足->也就是n个数肯定全部满足
所以答案就是(x,y)的对数*n
->O(n^2)
代码
void solve(){
cin>>n;
vector<int> a(2*n+1,0),b(2*n+1,0),c(2*n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<=n;i++) cin>>c[i];
for(int i=1;i<=n;i++) a[i+n]=a[i];
for(int i=1;i<=n;i++) b[i+n]=b[i];
for(int i=1;i<=n;i++) c[i+n]=c[i];
vector<bool> is_ok_ab(n+1,1),is_ok_bc(n+1,1);
for(int x=0;x<n;x++){//偏移量
for(int p=1;p<=n;p++){//a的每个位置
if(a[p]>=b[p+x]){
is_ok_ab[x]=0;
break;
}
}
}
for(int y=0;y<n;y++){//偏移量
for(int p=1;p<=n;p++){//b的每个位置
if(b[p]>=c[p+y]){
is_ok_bc[y]=0;
break;
}
}
}
i64 x=0,y=0;
for(int i=0;i<n;i++) if(is_ok_ab[i]) x++;
for(int i=0;i<n;i++) if(is_ok_bc[i]) y++;
i64 ans=n*x*y;
cout<<ans<<endl;
}
小红的神秘密码解锁
https://ac.nowcoder.com/acm/contest/127264/D
题目大意

思路
WA解:不可能连跨3个组 就一定是两个连续组之间的构造
hack:跨组 001100110011001100 -> 001101001100001100
翻转操作只影响区间内的字符,颜色块数量的变化仅由区间两端与外部字符的连接情况决定->只看区间左右交界处的变化

其实只有1和-1两种情况 不可能相等
将区间分为四类:
1.整个区间 [1, n]:总是满足,贡献 1
2.左端点为 1,右端点小于 n:需要 Δ右(r) = 0->不可能
3.右端点为 n,左端点大于 1:需要 Δ左(l) = 0->不可能
4.左端点大于 1 且右端点小于 n:需要 Δ左(l) + Δ右(r) = 0->前后缀统计
AC代码
const int N=3e5+10;
int n;
string s;
//和内部的都没关系,只和两个边界有关系,找△=0的
void solve(){
cin>>s;
n=s.size();
vector<i64> left(n,0),right(n,0);
//情况1:全选
i64 ans=1LL;
/*左边: 01 -> 00 -1
00 -> 01 1
*/
for(int i=1;i<n;i++){
if(s[i]==s[i-1]) left[i]=1;
else left[i]=-1;
}
//右边同理
for(int i=0;i<n-1;i++){
if(s[i]==s[i+1]) right[i]=1;
else right[i]=-1;
}
//情况2:l选1 情况3:r选n->一定选不到另一个△为0的
//情况4:l不选1 r不选n 那么只能1和-1凑
vector<i64> r1(n+1,0),rfu1(n+1,0);
for(int i=n-2;i>=0;i--){
if(right[i]==1){
r1[i]=r1[i+1]+1;
rfu1[i]=rfu1[i+1];
}
else{
rfu1[i]=rfu1[i+1]+1;
r1[i]=r1[i+1];
}
}
for(int i=1;i<n;i++){
if(left[i]==1) ans+=rfu1[i];
else ans+=r1[i];
}
cout<<ans<<endl;
}
Card Game
https://ac.nowcoder.com/acm/contest/120561/B
读题要认真
题目大意
有 \(2n\) 张牌,牌上的数字恰好构成 \(1,2,\dots,2n\) 的一个排列。
初始时,这些牌被平均分成两组(每组 \(n\) 张),分别作为小苯的手牌数组 \(a\) 和小红的手牌数组 \(b\) (小红的牌序固定)。
小苯可以在游戏开始前任意重排自己的手牌顺序。游戏规则如下:
- 若其中一人已无手牌,游戏结束。
- 两人各打出当前手牌的第一张牌,数字较大的一方得1分,并将自己打出的牌移除;另一方的牌保留在手牌中。
小苯的目标是通过重排手牌,让自己的得分尽可能高。
请你计算:有多少种重排 \(a\) 的方式,能让小苯获得这个“最高得分”?
答案需对 \(998244353\) 取模后输出。
思路
只和a的次序 和 \(min_b\)有关
小牌一直不会被杀,大牌赢一次就会被杀

代码
int n;
void solve(){
cin>>n;
vector<i64> a(n+1,0),b(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
i64 bmn=1e9;
for(int i=1;i<=n;i++) bmn=whink_min<i64>(bmn,b[i]);
int s=0;
for(int i=1;i<=n;i++){
if(a[i]>bmn) s++;
}
i64 ans=fact[s]*fact[n-s]%mod;
cout<<ans<<endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号