面试常考各类排序算法总结.(c#)

前言

面试以及考试过程中必会出现一道排序算法面试题，为了加深对排序算法的理解，在此我对各种排序算法做个总结归纳。

1、冒泡排序算法(BubbleSort)

1.1 算法描述

（1）比较相邻的元素。如果第一个比第二个大，就交换他们两个。

（2）对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

（3）针对所有的元素重复以上的步骤，除了最后一个。

（4）持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

  最好时间复杂度O（n） 最坏时间复杂度O（n2）

1.2 动图演示

1.3 C#代码实现

public Class SortDemo
{
     public void BubbleSort(int[] arr)
     {
            int temp=0;
          //需要走arr.Length-1 趟
           for(int i=0;i<arr.Length-1;i++)
           {
                 //每一趟需要比较次数
                 for(int j=0,j<arr.Length-i-1;j++)
                 {
                     //升序排序
                      if(arr[j]>arr[j+1])
                      {
                               temp=arr[j];//将较大的变量保存在临时变量
                               arr[j]=arr[j+1]；
                               arr[j+1]=temp;
                       }   
                 }
            }
         
     }
}

 

2、直接插入排序(InsertionSort)

2.1 算法描述

（1）从第一个元素开始，该元素可以认为已经被排序；

（2）取出下一个元素，在已经排序的元素序列中从后向前扫描；

（3）如果该元素（已排序）大于新元素，将该元素移到下一位置；

（4）重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；

（5） 将新元素插入到该位置后；

（6）重复步骤2~5。

2.2 动图演示

2.3 C#代码实现

public Class SortDemo
{
      public void InsertionSort(int[] arr)
      {
             int temp=0;
             //遍历待插入的数(从第二位开始)
             for(int i=1;i<arr.Length;i++)
             {

　　　　　　　　　　　　temp=arr[i];//待插入的数

　　　　　　　　　　　　int j=i-1;//（j为已排序的待插入的位置序号）
                     
                     //若已排序的数大于待插入数，则往后移一位
                     while(j>=0&&arr[j]>temp)
                     {
                            arr[j+1]=arr[j];
                            j--;
                      }
                     arr[j+1]=temp;//将待插入的数放入插入位置
              }
      }
}

3、选择排序(SelectionSort)

3.1 算法描述

 选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 

（1）初始状态：无序区为R[1..n]，有序区为空；

（2）第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；

（3）n-1趟结束，数组有序化了。

3.2 动图演示

3.3 C#代码实现

public void SelectionSort(int[] arr)
     {
         int temp;
         for(int i=0;i<arr.Length-1;i++)
         {
             int minVal=arr[i];
             int minIndex=i;
             for(int j=i+1;j<arr.Length;j++)
             {
                 if(minVal>arr[j])
                 { 
                    minVal=arr[j];
                    minIndex=j;
                 }
             }
             temp=arr[i];
             arr[i]=minVal;
             arr[minIndex]=temp;
         }
 
     }
}

 4、快速排序(QuickSort)

4.1 算法描述

（1）从数列中挑出一个元素，称为 “基准”（pivot）；

（2）重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

（3）递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

   快速排序法是采用递归的方式对待排序的数列进行若干次的操作,每次操作使得被操作的数列部分以某个元素为分界值分成两部分,一部分小于该分界值,另一部分大于该分界值.该分界值一般被称为"枢轴". 一般先以左边第一个数作为分界值，将数列按该分界值分成左右两 部分，左边部分小于该分界值，右边部分大于该分界值，然后再对左右两部分做重复的操作，直到最后完成排序。

  以数列 14,11,25,37,9,28 为例,详细描述执行一趟快速排序的算法:

      1,选择待排序数列的枢轴,一般以数列的首元素作为枢轴.此数列中,我们选择首元素14作为枢轴,nPivot = 14.

      2,设定两个指针 i 和 j ,分别指向数列的首元素和尾元素. i 指向首元素14, j 指向尾元素28.示意图如下:

               

      3,向前移动尾指针 j ,使其指向从数列尾部算起首个小于枢轴(即14)的元素,并将该元素置换到头指针 i 指向的位置._nArray[i] =_nArray[j].示意图如下:

         

      首次执行该操作时 i 指针指向处的值实际上就是枢轴的值,此处的操作可以理解为 i 指针指向处的值已在之前被置换到枢轴中,此时, i 指向处已经是一个空位,在此时用找到的小于枢轴的元素填在此处.

      4,向后移动头指针 i ,使其指向从数列头部算起首个大于枢轴(即14)的元素,并将该元素置换到尾指针 j 指向的位置._nArray[j] =_nArray[i].示意图如下:

               

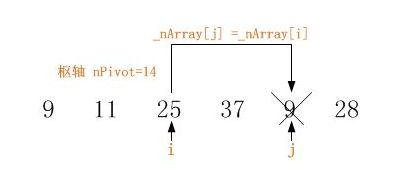
      此处同样可以理解为 j 指针指向处的值已在上一步操作中置换了出去. j 处已是一个空位.

      5,如此重复执行步骤3和步骤4,直至 i==j 时结束该循环.

      6,退出了该循环后, i 与 j 必定指向同一位置.在该位置的前部元素,其值均小于枢轴.而在该位置的后部元素,其值均大于枢轴.显而易见,此时 i 和 j 同时指向的位置就应该是枢轴的"新家"._nArray[i]=nPivot.如下图:

               

      至此,一趟排序结束.待排序数列的首元素将该数列分成了比其小和比其大的两部分.如下图:

         

      接着,我们对这一大一小两部分子数列执行相同的排序操作.

      如此"递归",直至对整个数列完成排序操作.

4.2 动图演示

4.3 c#代码实现

class Program

{

      static void Main(string[] args)

      {

        Console.WriteLine("请输入待排序数列(以\",\"分割):");

        int[] arr = new int[] { 10, 11, 44, 9, 8, 19, 45, 20, 24, 11, 3, 7 };

        Sort(arr, 0, arr.Length - 1);

        foreach (var i in arr)

        {

         Console.WriteLine(i.ToString());

        }

       }

/// <summary>
        /// 排序
        /// </summary>
        /// <param name="array">要排序的数组</param>
        /// <param name="low">下标开始位置，向右查找</param>
        /// <param name="high">下标开始位置，向左查找</param>
        public static void Sort(int[] array, int low, int high)
        {
  if (low >= high)
   return;
  //完成一次单元排序
  int index = SortUnit(array, low, high);
  //递归调用，对左边部分的数组进行单元排序
  Sort(array, low, index - 1);
  //递归调用，对右边部分的数组进行单元排序
  Sort(array, index + 1, high);
    }
 /// <summary>
/// 单元排序
        /// </summary>
        /// <param name="array">要排序的数组</param>
        /// <param name="low">下标开始位置，向右查找</param>
        /// <param name="high">下标开始位置，向右查找</param>
        /// <returns>每次单元排序的停止下标</returns>
        public static int SortUnit(int[] array, int low, int high)
        {
 int key = array[low];//基准数
  while (low < high)
  {
   //从high往前找小于或等于key的值
   while (low < high && array[high] > key)
     high--;
   //比key小开等的放左边
   array[low] = array[high];
   //从low往后找大于key的值
   while (low < high && array[low] <= key)
    low++;
   //比key大的放右边
   array[high] = array[low];
 }
            //结束循环时，此时low等于high，左边都小于或等于key，右边都大于key。将key放在游标当前位置。 
  array[low] = key;
  return high;
        }

}

文章参考摘自：https://www.cnblogs.com/yundan/p/4022056.html   https://www.cnblogs.com/geduocoding/p/7097870.html