网络剪枝 -- 理论
剪枝分类
从network pruning 的粒度来说,可以分为结构化剪枝(structured pruning) 和非结构化剪枝(Unstructured pruning) 两类
-
早期的一些方法是基于非结构化的, 它裁剪的粒度为单个神经元。
如果对kernel进行非结构化剪枝,则得到的kernel是稀疏的,即中间有元素为0的矩阵。除非下层的硬件和计算库对其有比较好的支持,pruning后版本很难得到实质的性能提升。稀疏矩阵无法利用现有的BLAS库获得额外性能收益。 -
结构化剪枝。 结构化剪枝没有改变权重矩阵本身的稀疏程度,现有的计算平台和框架都可以实现很好的支持。
structured pruning又可以细分:channel-wise、filter-wise还可以是shape-wise
非结构化剪枝
修剪连接的最大优势是它们是网络中最小、最基本的元素,因此,它们的数量足以在不影响性能的情况下大量修剪它们。如此精细的粒度允许修剪非常细微的模式,例如,最多可修剪卷积核内的参数。由于修剪权重完全不受任何约束的限制,并且是修剪网络的最佳方式,因此这种范式称为非结构化剪枝。
然而,这种方法存在一个主要的、致命的缺点:大多数框架和硬件无法加速稀疏矩阵计算,这意味着无论你用多少个零填充参数张量,它都不会影响网络的实际成本。然而,影响它的是以一种直接改变网络架构的方式进行修剪,任何框架都可以处理。
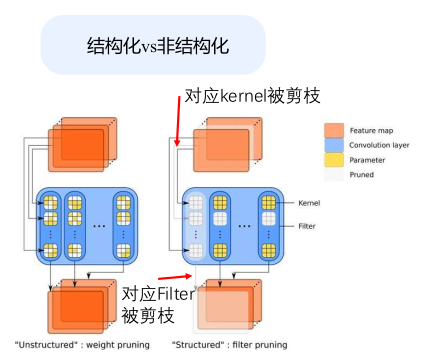
非结构化(左)和结构化(右)剪枝的区别:结构化剪枝去除卷积滤波器和内核行,而不仅仅是剪枝连接。这导致中间表示中的特征图更少。
1、权重剪枝(weights剪枝)
最原始的权重剪枝
将权重矩阵中相对不重要的权值剔除,然后再重新精修(finetune)网络进行微调。
剪掉神经元节点之间的不重要的连接。相当于把权重矩阵中的单个权重值设置为0,一般的,会对权重矩阵中所有的数值按照大小排序,把排在后面的一定比例的值设为0即可。
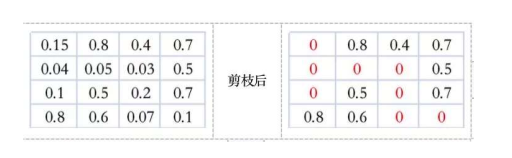
这种权重剪枝导致产生非结构化稀疏的filters,这很难被通用硬件加速。
注:虽然权重剪枝在parameters上的确没有减少,但是FLOPs减少了,所以仍然起到了压缩模型大小,降低Inference latency的效果。
Weights Pruning是一种细粒度的剪枝方法,它对网络内部的单个权值进行剪枝,在不牺牲Accuracy的情况下形成稀疏网络。
细粒度级的稀疏性使其提供了最高的灵活性,通用性导致了更高压缩率, 然而,由于非零的位置权重是不规则的,需要额外的权重记录位置信息,并且由于网络内部的随机性,WP修剪后的稀疏网络不能像FP(Filters Pruninng)那样以结构化的方式表示,使得权重剪枝无法在通用处理器上实现加速。
2、神经元(Activation)剪枝
Activation pruning中比较经典的方法有:
Network trimming: A data-driven neuron pruning approach towards efficient deep architectures,
这是2017年Hu等人发表在ICLR上的工作。这篇论文中用activations中0的比例 (Average Percentage of Zeros, APoZ)作为度量标准,
An Entropy-based Pruning Method for CNN Compression,则利用信息熵进行剪枝。文章针对VGG16和ResNet18采用了两个不同的裁剪策略。对VGG16:
- 裁剪前十层的layer
- 用最大平均池化代替全连接层
把权重矩阵中某个神经元节点去掉,则和神经元相连接的突触也要全部取出。相当于同时去除权重剪枝中的某一行和列。
如何判断神经元节点的重要程度呢?
可以通过神经元对应的行和列的权重值的平方和的根的大小进行排序,把排序在后面一定比例的神经元节点去掉。
结构化剪枝
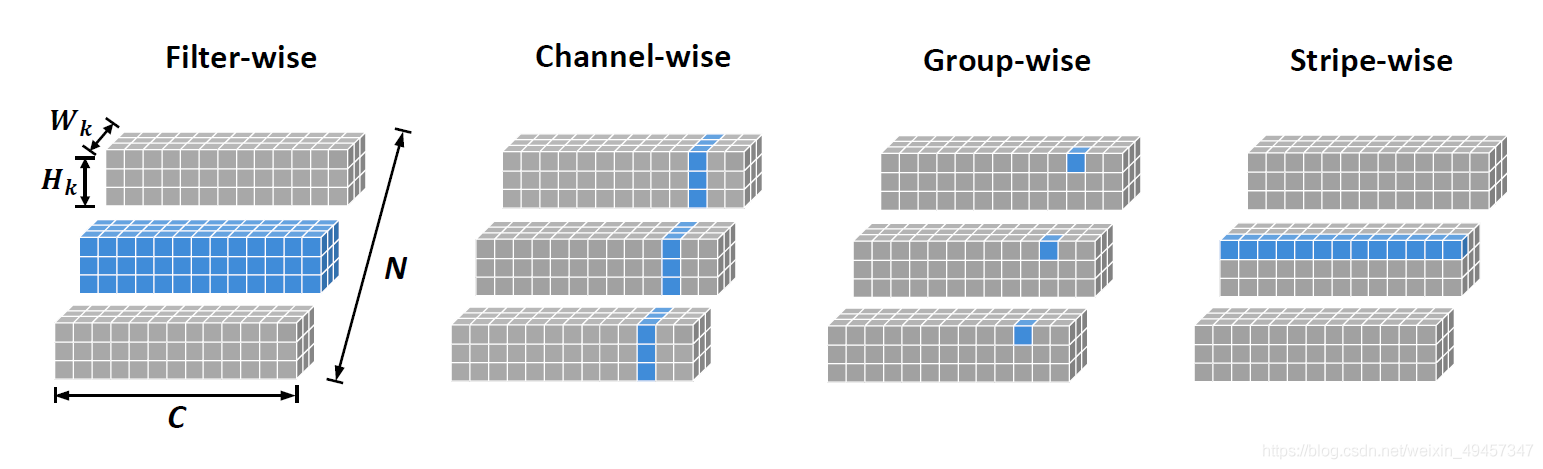
1、filter-wise
一个卷积核被剪枝,那么其前一个Feature Map 和 下一个Feature Map 都会发生相应的变化。
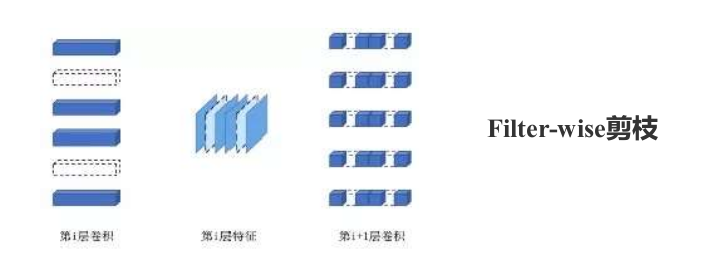
以上图为例,在第 i 层卷积中, 其中第2、5个卷积核被剪掉(卷积核数量减少,每个卷积核的shape不变); 当i - 1层的featuremap经过第i层feature map,其中的第2、5个channel也相应的被去除。
为了匹配第i层featuremap通道维度产生的变化,第i+1层的卷积中的每个卷积核的第2、5个channel 的权重被去除(卷积核数量不变,但每个卷积的shape发生变化)。
单层中卷积核剪枝
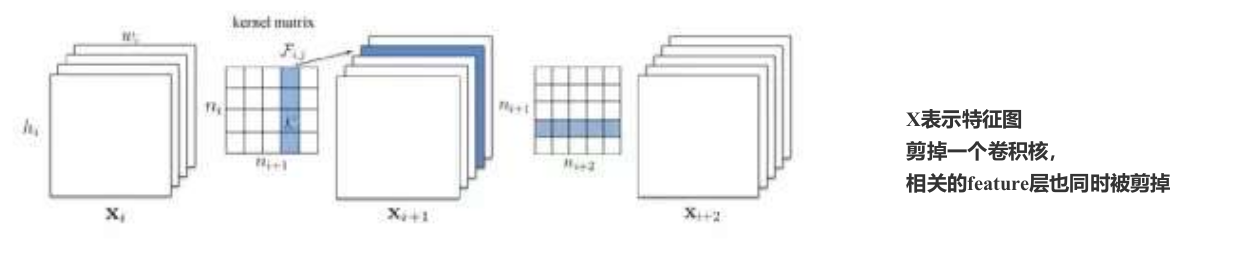
如上图,kernel matrix中的\(n_i\)表示第i层feature map的通道深度;\(n_{i+1}\)表示i + 1层feature map的通道深度。kernel matrix中每个卷积核的尺寸为k * k
从第i个卷积层剪掉n个卷积核的算法过程如下:
-
1、计算每个卷积核的权重绝对值之和
-
2、根据值大小排序
-
3、将最小的n个卷积核及对应的featrue map剪掉,下一个卷积层中相关的卷积核也要移除。
-
4、生成了第
i层和第i+1层新的权重矩阵,剩余的权重参数被复制到新模型中。
2、Channel-wise
以《Learning Efficient Convolutional Networks Through Network Slimming》为例。
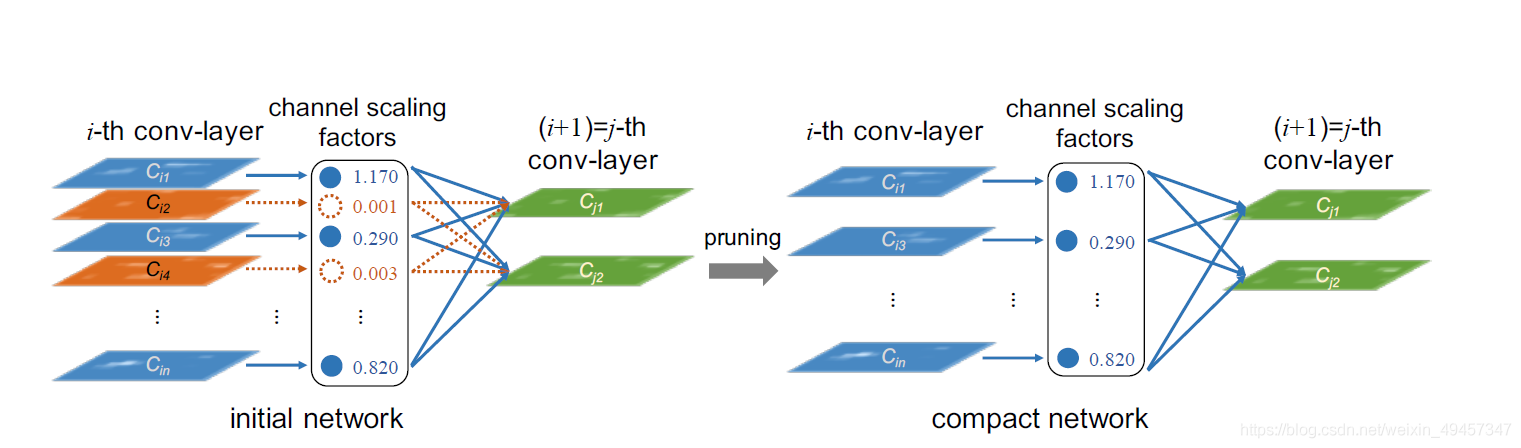
conv-layer的每个channel的重要程度可以和batchnorm层关联,如果某个channel后的batchnorm层中对应的scaling factor足够小,则说明该channel的重要程度低,可以忽略,如下图中橙色的两个通道被剪枝。
batchnorm的公式如下:
其中$ \gamma $表示channel scaling factors
为了增加稀疏程度,方便对channel进行剪枝,训练时需要对每个batchnom层的scaling factor增加L1的约束。channel-wise和filter-wise既有区别也有联系,两者使用的剪枝评判方法不同,但最终都会体现在对卷积核或卷积核中某些layer的剪枝。
3、Group-wise
Group-wise就是对通道的分组剪枝,如封图所示,对通道进行分组剪枝其实已经是一个改进的方法了。但是他也有一个明显的弊端。
就是他移除的是某一层中所有的filters相同位置上的权重。但是,每个filters中无效的权重位置可能不同,所以这个方法解决不了这一点。
CVPR 2016的《Fast convnets using group-wise brain damage》和NIPS 2016的《Learning structured sparsity in deep neural networks》介绍了对通道进行分组剪枝的概念,如上图,提出通过group lasso regularization来学习神经网络中的结构化稀疏性。可以看到,分组后每次剪枝都是对每一层中filter的同一个位置剪去,使用“im2col”实现作为过滤器式和通道式修剪,可以有效地处理分组式修剪。
4、Stripe-wise
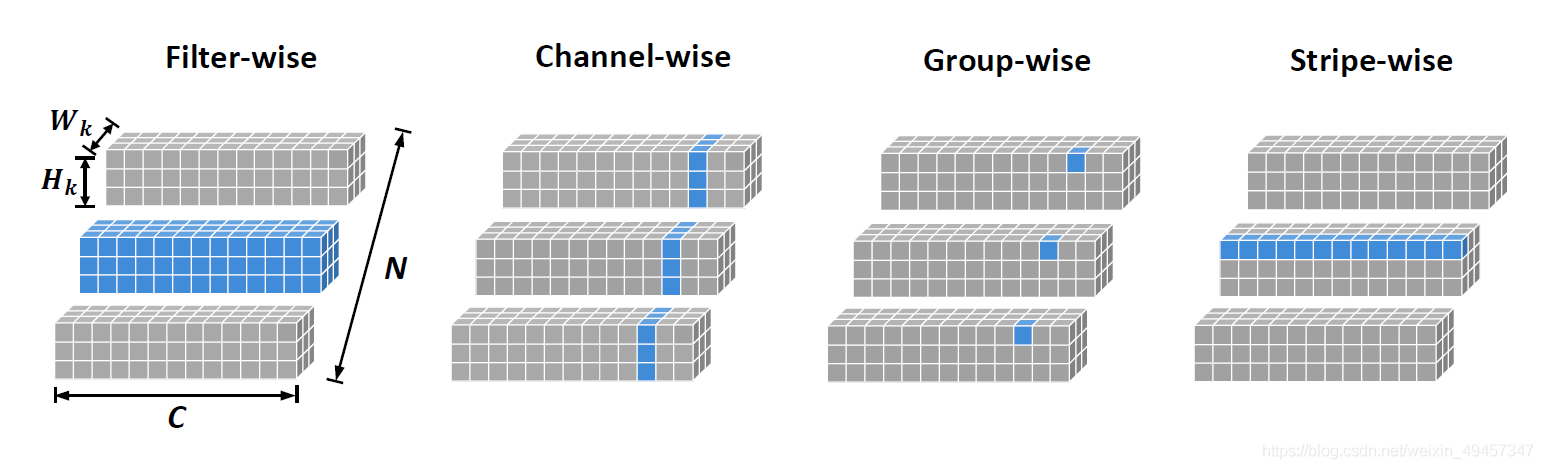
它是结合了两种结构化和非结构化剪枝中的典型方法——weights pruning 和 filters pruning。所以它的做法是在filters中剪枝filter。如上图所示,他是按照kernel size把原filter切分成一个个条状的小条纹。
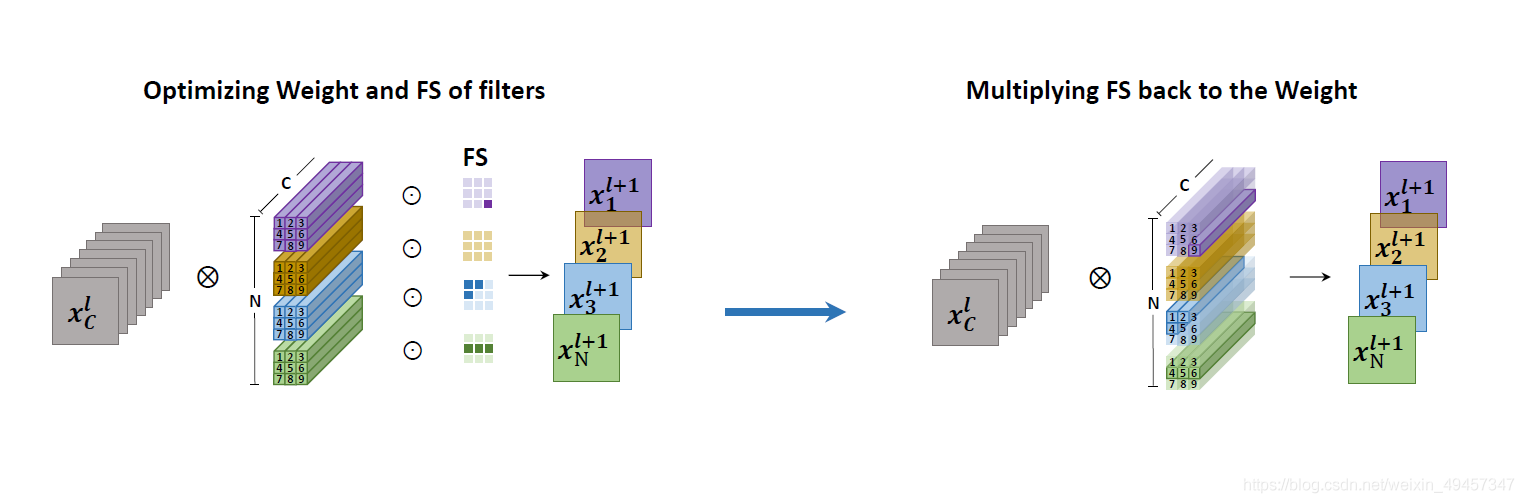
比如一个kernel,它的长和宽是经常相等的,假设是k×k×c,那我们就可以按照他的size把它剪成k×k个条。而且结合paper中提出的框架,可以学习到这个最佳形状的条纹。
剪枝标准
权重大小标准
一个非常直观且非常有效的标准是修剪绝对值(或“幅度”)最小的权重。实际上,在权重衰减的约束下,那些对函数没有显着贡献的函数在训练期间会缩小幅度。因此,多余的权重被定义为是那些绝对值较小的权重。尽管它很简单,但幅度标准仍然广泛用于最新的方法 ,使其成为该领域的主要内容。
然而,虽然这个标准在非结构化剪枝的情况下实现起来似乎微不足道,但人们可能想知道如何使其适应结构化剪枝。一种直接的方法是根据过滤器的范数(例如 L 1 或 L 2)对过滤器进行排序 。如果这种方法非常简单,人们可能希望将多组参数封装在一个度量中:例如,一个卷积过滤器、它的偏差和它的批量归一化参数,或者甚至是并行层中的相应过滤器,其输出随后被融合。
一种方法是在不需要计算这些参数的组合范数的情况下,在要修剪的每组图层之后为每个特征图插入一个可学习的乘法参数。当这个参数减少到零时,有效地修剪了负责这个通道的整套参数,这个参数的大小说明了所有参数的重要性。因此,该方法包括修剪较小量级的参数 。
梯度幅度剪枝
权重的大小并不是唯一存在的流行标准(或标准系列)。实际上,一直持续到现在的另一个主要标准是梯度的大小。事实上,早在 80 年代,一些基础工作 通过移除参数对损失的影响的泰勒分解进行了理论化,一些从反向传播梯度导出的度量可以提供一种很好的方法来确定 可以在不损坏网络的情况下修剪哪些参数。
该方法 的最新的实现实际上是在小批量训练数据上累积梯度,并根据该梯度与每个参数的相应权重之间的乘积进行修剪。该标准也可以应用于上述参数方法。
全局或局部剪枝
要考虑的最后一个方面是所选标准是否是全局应用于网络的所有参数或过滤器,或者是否为每一层独立计算。虽然多次证明全局修剪可以产生更好的结果,但它可能导致层崩溃 。避免这个问题的一个简单方法是采用逐层局部剪枝,即在使用的方法不能防止层崩溃时,在每一层剪枝相同的速率。
本处对剪枝做个初步的了解,后续会对其进行更深的了解学习
参考:
https://cloud.tencent.com/developer/article/1877711
https://blog.csdn.net/weixin_49457347/article/details/117110458



