决策树

决策树是一种多功能机器学习算法，即可以执行分类任务也可以执行回归任务，甚至包括多输出（multioutput）任务。决策树是随机森林的基本组成部分（当今最强大的机器学习算法之一）

决策树的训练与可视化

在鸢尾花数据集上进行一个决策树分类器的训练

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
X = iris.data[:,2:]#petal length (cm),petal width (cm)
y = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X,y)

可视化

from sklearn.tree import export_graphviz
import graphviz

iris_tree = export_graphviz(tree_clf,
               feature_names=iris.feature_names[2:],
               class_names=iris.target_names,
               rounded=True,
               filled=True)
graphviz.Source(iris_tree)

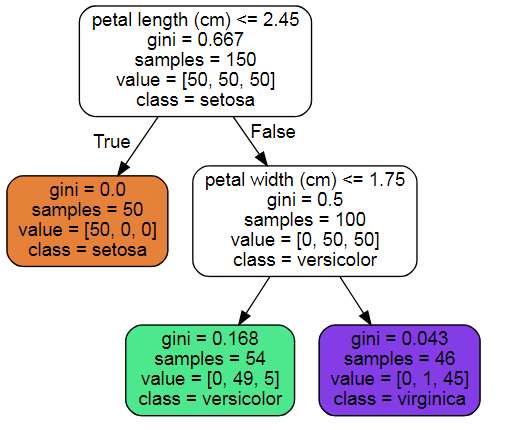
节点的samples属性统计出它应用于多少个训练样本实例
节点的value属性说明这个节点对于每一个类别的样例有多少个
节点的Gini属性用于测量它的纯度，如果一个节点包含的所有训练样例全都是同一类别的，就说这个节是纯的（Gini=0）

估计分类概率

决策树还可以估计某个实例输入特定类K的概率，首先遍历树来查找此实例的叶节点，然后返回此节点中类k的训练实例的比例。

CART训练算法

Scikit_Learn用分裂回归树（Classifier And Regression Tree，简称CART）算法训练决策树（也叫“增长树”），算法思想如下：
首先使用单个特征K和阈值\(t_k\)(例如，“花瓣长度<= 2.45cm”)将训练集分为两个子集。
那它是如何选择k和\(t_k\)呢？

他寻找能够产生最纯粹的子集一对（k,\(t_k\)）,然后通过子集大小加权计算。

算法会尝试最小化成本函数。公式如下：

当它成功的将训练集分为两部分后，它会继续使用相同的递归式逻辑继续的分割子集，然后是子集的子集。当达到预定的最大深度之后将会停止分裂（由max_depth超参数决定），后者是它找不到可以继续降低不纯度的分裂方法的时候。（min_samples_split,min_samples_leaf,min_weight_fraction_leaf,max_leaf_nodes）等几个超参数控制了其他的停止生长条件。

CART算法是一种贪婪算法，它贪婪地搜索最高级别的最佳分割方式，然后在每个深度重复该过程。它不检查分割是否能够在几个级别中的全部分割可能中找到最佳方法。贪婪算法通常会产生一个相当好的解决方法，但它不保证这是全局中最佳的解决方案。

基尼不纯度或信息熵

算法使用Gini不纯度来进行检测，也可以使用标准超参数设置为“entropy”来计算熵不纯度进行检测。

熵，源于热力学中分子混乱程度的概念，当分子井然有序的时候，熵接近0

在机器学习中，熵通常被用来作为不纯度的衡量方式，当一个集合内包含一类实例时，我们称为数据集的熵为0。（熵的减少通常称为信息增益）

那是使用Gini指数呢还是熵呢？
事实上，大部分情况下两者是没有多大差别的，他们都会生成类似的决策树。但有时候也会产生不同的树：基尼指数会趋于在树的分支中将最多的类隔离出来，而熵指数趋向于产生略微平衡一点的决策树模型。
不过，基尼指数还有个优点，那就是计算稍微快一点。

正则化超参数

决策树几乎不对训练数据做任何假设（与此相反的是线性回归等模型，这类模型通常会假设数据是符合线性关系的）
如果不添加约束，树结构模型通常根据训练数据调整自己，使自身能够很好的拟合数据，而这种情况下大多数会导致模型过拟合。这类模型通常会被称为非参数模型，这不是因为没有任何参数（通常也有很多），而是因为在训练之前没有确定参数的具体数量，所以模型结构可以根据数据的特征自由生长。
与此相反的是，像线性回归这样的参数模型有事先定义好的参数数量，所以自由度是受限的，这样虽然减少了过拟合的风险，但同时也增加了欠拟合的风险。
DecisionTreeClassifier类还有一些其他的参数用于限制树模型的形状：

min_samples_split:节点在分裂前必须具有的最小样本数
min_samples_leaf:叶节点必须具有的最小样本数
min_weight_fraction_leaf(和min_samples_leaf类似)：表示为加权总数的一小部分实例
max_leaf_nodes:叶节点的最大数量
max_features:在每个节点被评估是否分裂的时候，具有最大特征数量
增加min_* 超参数或减少max_* 超参数 会使模型正则化

回归

造数据

import numpy as np

np.random.seed(42)
m = 200
x = np.random.rand(m,1)
y = 4 * (x -0.5) ** 2
y = y+ np.random.randn(m,1)/10

进行预测

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor(max_depth=2,random_state=42)
tree_reg.fit(X,y)

可视化显示

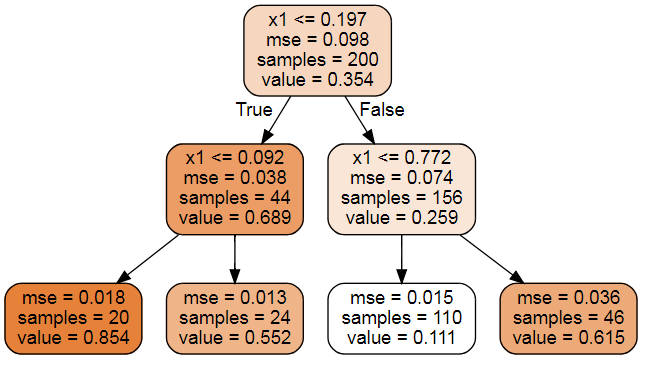
iris_reg= export_graphviz(tree_reg,feature_names=["x1"],class_names=iris.target_names,rounded=True,filled=True)
graphviz.Source(iris_reg)

不稳定行

决策树的特点：

• 容易理解和解释，易于使用且功能丰富而强大。

限制：

• 决策树非常喜欢设定正交化的决策边界，（所有边界都是和某一个轴相垂直的），这使得它对训练数据集的旋转非常敏感。解决这个问题，可以使用PCA主成分分析法，这通常可使训练结果变的更好一点。
  通俗的讲，决策时的主要问题是它对训练数据的微小变化非常敏感。事实上，由于Scikit_Learn的训练算法是非常随机的，即使是相同的训练数据也可能得到差别很大的模型（除非设立了随机种子），也可使用随机森林通过多棵树的平均预测值限制这种不稳定性。