非线性支持向量机分类
处理非线性数据时,线性回归中,通过对特征数据进行加权获得新的特征(通过sklearn.preprocessing 中的PolynomialFeatures),实现对非线性数据的分类。同样在SVM中对非线性分类也可同样采用此方法。
在sklearn提供的卫星数据集来进行测试。创建一个流水线(Pipeline)包含多项式特征(PolynomialFeatures)变换,然后一个标准化(StandardScaler)和分类器(LinearSVC)。
加载数据
from sklearn.datasets import make_moons
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
X,y = make_moons(n_samples=100,noise=0.15,random_state=42)
def plot_dataset(X,y,axes):
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
plt.axis(axes)
plt.grid(True,which='both')
plt.xlabel(r'$x_1$',fontsize=20)
plt.ylabel(r'$x_2$',fontsize=20)
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()
效果展示:

训练
对数据进行多项式特征转换、标准化以及分类
polynomial_svm_clf = Pipeline([
('poly_feature',PolynomialFeatures(degree=3)),
('scaler',StandardScaler()),
('svm_clf',LinearSVC(C=10,loss='hinge',random_state= 42))
])
polynomial_svm_clf.fit(X,y)

查看分类效果:
def plot_predictions(clf,axes):
x0s = np.linspace(axes[0],axes[1],100)
x1s = np.linspace(axes[2],axes[3],100)
x0,x1 = np.meshgrid(x0s,x1s)
X = np.c_[x0.ravel(),x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2)
plt.contourf(x0,x1,y_decision,cmap=plt.cm.brg,alpha=0.1)
plot_predictions(polynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()
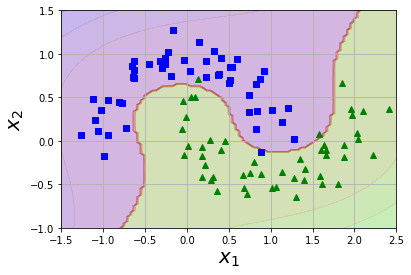
添加多项式特征很容易实现,不论是SVM,还是在各种机器学习算法都有非常不错的表现,但低次数的多项式不能处理非常复杂的数据集,而高次数的多项式的多项式却产生了大量的特征,会使模型变的慢。
此时,就引入了本小节的神技“核技巧(kernel trick)”,它可以取的像添加了许多多项式,甚至有高次数的多项式,一样好的结果。所以不会大量特征导致组合爆炸,因为并没有添加任何特征。可以使用SVC类来进行实现。
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='poly',degree=3,coef0=1,C=5))
])
poly_kernel_svm_clf.fit(X,y)
SVC()相关参数
C (float参数 默认值为1.0)
表示错误项的惩罚系数C越大,即对分错样本的惩罚程度越大,因此在训练样本中准确率越高,但是泛化能力降低;相反,减小C的话,容许训练样本中有一些误分类错误样本,泛化能力强。对于训练样本带有噪声的情况,一般采用后者,把训练样本集中错误分类的样本作为噪声。
**kernel **(str参数 默认为‘rbf’)
该参数用于选择模型所使用的核函数,算法中常用的核函数有:
-- linear:线性核函数
-- poly:多项式核函数
--rbf:径像核函数/高斯核
--sigmod:sigmod核函数
--precomputed:核矩阵,该矩阵表示自己事先计算好的,输入后算法内部将使用你提供的矩阵进行计算
**degree **(int型参数 默认为3)
该参数只对'kernel=poly'(多项式核函数)有用,是指多项式核函数的阶数n,如果给的核函数参数是其他核函数,则会自动忽略该参数。
gamma (float参数 默认为auto)
该参数为核函数系数,只对‘rbf’,‘poly’,‘sigmod’有效。如果gamma设置为auto,代表其值为样本特征数的倒数,即1/n_features,也有其他值可设定。
coef0:(float参数 默认为0.0)
该参数表示核函数中的独立项,只有对‘poly’和‘sigmod’核函数有用,是指其中的参数c。
probability( bool参数 默认为False)
该参数表示是否启用概率估计。 这必须在调用fit()之前启用,并且会使fit()方法速度变慢。
shrinkintol: float参数 默认为1e^-3g(bool参数 默认为True)
该参数表示是否选用启发式收缩方式。
tol( float参数 默认为1e^-3)
svm停止训练的误差精度,也即阈值。
cache_size(float参数 默认为200)
该参数表示指定训练所需要的内存,以MB为单位,默认为200MB。
class_weight(字典类型或者‘balance’字符串。默认为None)
该参数表示给每个类别分别设置不同的惩罚参数C,如果没有给,则会给所有类别都给C=1,即前面参数指出的参数C。如果给定参数‘balance’,则使用y的值自动调整与输入数据中的类频率成反比的权重。
**verbose **( bool参数 默认为False)
该参数表示是否启用详细输出。此设置利用libsvm中的每个进程运行时设置,如果启用,可能无法在多线程上下文中正常工作。一般情况都设为False,不用管它。
**max_iter **(int参数 默认为-1)
该参数表示最大迭代次数,如果设置为-1则表示不受限制。
random_state(int,RandomState instance ,None 默认为None)
该参数表示在混洗数据时所使用的伪随机数发生器的种子,如果选int,则为随机数生成器种子;如果选RandomState instance,则为随机数生成器;如果选None,则随机数生成器使用的是np.random。
参考:https://www.jianshu.com/p/a9f9954355b3
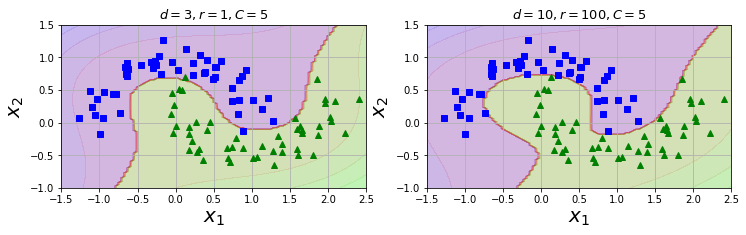
下图将10阶的与3阶的多项式核SVM分类器进行比较。10阶的分类器模型出现了明显的过拟合现象,此时应减小多项式核的阶数。参数数coef0控制高阶多项式与低阶多项式对模型的影响。
增加相似特征
另一个解决非线性问题的方法是使用相似函数(similarity function)计算每个样本与特定地标(landmark)的相似度。其中需要定义一个相似函数--高斯径向基函数(Gaussian Radial Basis Function,RBF),公式如下。
它在SVM上的神奇之处在于:高斯核让你可以获得同样好的结果称为可能,就像你在相似特征法添加了许多相似特征一样,但事实,并不需要再RBF添加
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
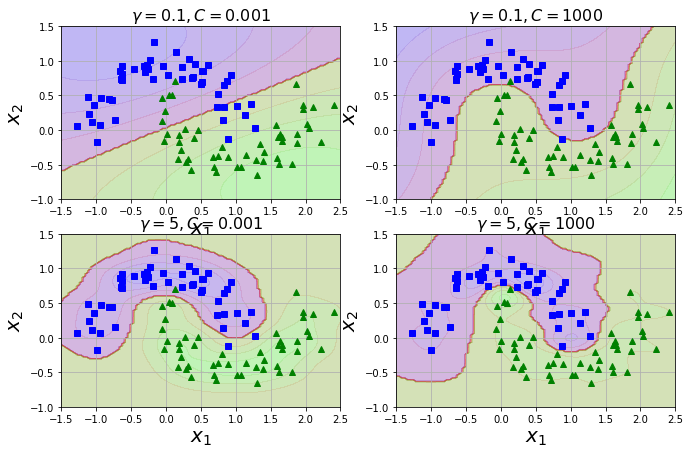
并使用不同的超参数gamma(\(\gamma\))和C训练的模型
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
plt.show()