线性模型的正则化
降低模型的过拟合的好方法就是正则化这个模型(即限制它):模型有越少的自由度,就越难拟合数据。例如,正则化一个多项式模型,一个简单的方法就是减少多项式的阶数。
对于线性模型,正则化的典型实现就是约束模型中参数的权重。这里介绍三种不同约束权重的方法:Ridge回归,Lasso回归和Elastic Net。但介绍之前,先了解下结构风险最小化和参数缩减(参考:https://blog.csdn.net/xmu_jupiter/article/details/46594273,https://blog.csdn.net/zhang_shuai12/article/details/53064697)
结构风险最小化是一种模型选择策略。模型选择的策略一般有两种:经验风险最小化和结构风险最小化。
模型f(x)关于训练数据集的平均损失称为经验风险或经验损失:\[R_{emp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) \]经验风险是模型关于训练样本集的平均损失。经验风险最小化(empirical risk minimization,EMP)的策略认为,经验风险最小的模型是最优的模型。根据这一策略,按照经验风险最小化求最优模型就是求解最优化问题,即求最小化\(R_{emp}(f)\)
当样本容量最够大时,经验风险最小化能保证有很好的学习效果,其中极大似然估计(MLE)就是一个经验风险最小化的一个例子。当模型是条件概率分布,损失函数是对数损失函数时,经验最小化等于极大似然估计。但样本容量很小时,经验风险最小化的效果并不好,因为所求取的参数是对于训练数据的无偏估计,结果就容易产生过拟合现象。
结构风险最小化就是为克服这过拟合而提出的。它是在经验风险最小化的基础上增加一个正则化因子,通常这个正则化因子时模型规模的函数,模型越复杂,这个函数取值越小。
正则化因子的加入其实可以解释为对模型参数进行了某种条件约束,然后参数的求解过程就相当于应用拉格拉日乘子法。通过对参数进行约束,保证了参数的取值不会太极端,也就进行了“参数缩减”。
岭(Ridge)回归
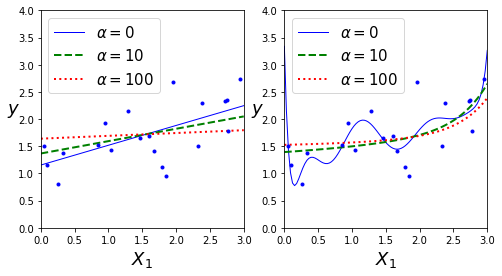
应用结构风险最小化的模型选择策略,在经验风险最小化的基础上加入正则化因子。当正则化因子选择为模型参数的二范数的时候,整个回归的方法就叫做岭回归。为什么叫“岭”回归呢?这是因为按照这种方法求取参数的解析解的时候,最后的表达式是在原来的基础上在求逆矩阵内部加上一个对角矩阵,就好像一条“岭”一样。加上这条岭以后,原来不可求逆的数据矩阵就可以求逆了。不仅仅如此,对角矩阵其实是由一个参数lamda和单位对角矩阵相乘组成。lamda越大,说明偏差就越大,原始数据对回归求取参数的作用就越小,当lamda取到一个合适的值,就能在一定意义上解决过拟合的问题:原先过拟合的特别大或者特别小的参数会被约束到正常甚至很小的值,但不会为零。
岭回归损失函数:
超参数\(\alpha\)决定了正则化这个模型的强度。如果\(\alpha=0\),那此时的岭回归就是了线性回归,如果\(\alpha\)非常大,所有的权重最后最后都接近于0,最后结果将是一条穿过数据平均值的水平直线。还需要注意的是偏差\(\theta_0\)是没有被正则化的(累加运算是从i=1开始的),如果定义w作为特征的权重向量(\(\theta_1到\theta_n\)),那么正则化可以简写成\(\frac{1}{2}(||w||_2)^2,||·||_2表示权重向量的l2范数\)
岭回归的封闭方程的解:
注意:
- 使用岭回归前,对数据进行缩放(可以使用StandardScaler)是非常重要的,算法对输入特征的术支持度(scale)非常敏感。大多数的正则化模型都是这样
- 一般情况下,训练过程使用的损失函数和测试过程中使用的评价函数是不一样的。除正则化外,还有一个不同,就是训练时损失函数应该在优化过程中易于求导,而在测试过程中,评价函数更应该解决最后的客观表现。一个好的例子,在分类训练中,使用对数损失作为损失函数,但却用精确度/召回率来作为它的评价函数
代码实现(借助sklearn)
代码:
m = 20
X = 3 * np.random.rand(m,1)
y = 1 + 0.5 * X + np.random.randn(m,1)/1.5
X_new = np.linspace(0,3,100).reshape(100,1)
def plot_model(model_class,polynomial,alphas,**model_kargs):
for alpha,style in zip(alphas,('b-','g--','r:')):
model = model_class(alpha,**model_kargs) if alpha>0 else LinearRegression()
if polynomial:
model = Pipeline([
('poly_features',PolynomialFeatures(degree=10,include_bias=False)),
('std_scaler',StandardScaler()),
('regul_reg',model)
])
model.fit(X,y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new,y_new_regul,style,linewidth=lw,label=r'$\alpha={}$'.format(alpha))
plt.plot(X,y,'b.',linewidth=3)
plt.legend(loc='upper left',fontsize = 15)
plt.xlabel('$X_1$',fontsize=18)
plt.ylabel('$y$',rotation=0,fontsize=18)
plt.axis([0,3,0,4])
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge,polynomial=False,alphas=(0,10,100),random_state=43)
plt.subplot(122)
plot_model(Ridge,polynomial=True,alphas=(0,10,100),random_state = 43)
plt.show()
可视化展示:
也可以使用sklearn对上述的封闭方程进行求解(使用Cholesky法进行矩阵分解)
ridge_reg = Ridge(alpha=1,solver='cholesky',random_state=42)
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]])
结果显示:
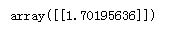
使用随机梯度下降法进行求解,其中penalty参数指的是正则化的惩罚类型,指定‘l2’表明在损失函数上加上一项:权重向量l2范数平方的一半,这是一简单的岭回归
sgd_reg = SGDRegressor(penalty='l2',max_iter=50,tol=-np.infty,random_state=42)
sgd_reg.fit(X,y.ravel())
sgd_reg.predict([[1.5]])
结果显示:
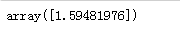
lasso回归
上面提到,岭回归是在结构风险最小化的正则化因子上使用模型参数向量的二范数形式,那,如果使用一范式形式就是lasso回归了。lasso回归相对于岭回归,会比较极端。它不仅可以解决过拟合问题,而且可以在参数缩减过程中将一些重复的不必要的参数直接缩减为0,也就是完全减掉了,这可以达到提取有用特征的作用。但是lasso回归的计算过程复杂,毕竟一范数不是连续可导的。
Lasso回归的损失函数:
Lasso回归子梯度向量:、
代码实现(借助sklearn)
代码:
from sklearn.linear_model import Lasso
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso,polynomial=False,alphas=(0,0.1,1),random_state=42)
plt.subplot(122)
plot_model(Lasso,polynomial=True,alphas =(0,10**-7,1),tol=1,random_state=42)
plt.show()
可视化展示:
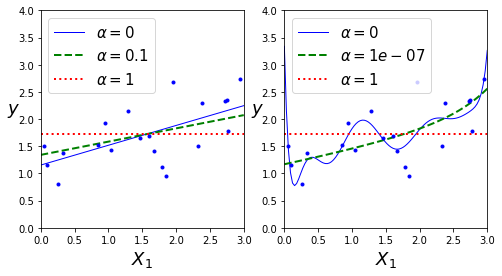
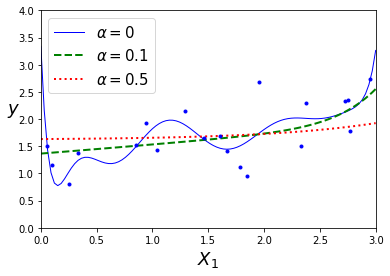
Lasso回归的一个重要特征就是它倾向于完全消除最不重要的特征的权重(即将它们设为0)。例如,右图中的虚线所示(\(\alpha=10^{-7}\)),曲线看起来像一条二次曲线,而且几乎是线性的,这是因为所有的高阶多项特征都被设为了0,换句话说,Lasso回归自动的进行特征选择同时输出一个稀疏模型(即,具有很少的非零权重)
为什么会出现这情况呢?可由下图进行解释:

在左上角图中,后背景的等高线(椭圆)表示了没有正则化的均方差损失函数(\(\alpha=0\)),白色的小圆圈表示在当前损失函数上批量梯度下降的路径。前背景的等高线(菱形)表示l1惩罚,黄色的三角形表示了仅在这个惩罚下批量梯度下降的路径(\(\alpha \rightarrow \infty\))。注意路径第一次是如何到达\(\theta_1=0\),然后向下滚动直到它到达\(\theta_2=0\)。在右上角图中,等高线表示的是相同损失函数再加上一个\(\alpha=0.5\)的l1惩罚。这幅图中,它的全局最小值在\(\theta_2=0\) 这根轴上。批量梯度下降首先到达 \(\theta_2=0\),然后向下滚动直到达到全局最小值。 两个底部图显示了相同的情况,只是使用了l2惩罚。 规则化的最小值比非规范化的最小值更接近于\(\theta=0\),但权重不能完全消除。
上述代码:
t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
# ignoring bias term
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[-1, 1], [-0.3, -1], [1, 0.1]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T)**2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])
def bgd_path(theta, X, y, l1, l2, core = 1, eta = 0.1, n_iterations = 50):
path = [theta]
for iteration in range(n_iterations):
gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + 2 * l2 * theta
theta = theta - eta * gradients
path.append(theta)
return np.array(path)
plt.figure(figsize=(12, 8))
for i, N, l1, l2, title in ((0, N1, 0.5, 0, "Lasso"), (1, N2, 0, 0.1, "Ridge")):
JR = J + l1 * N1 + l2 * N2**2
tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
levelsJ=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
levelsJR=(np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
levelsN=np.linspace(0, np.max(N), 10)
path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
path_JR = bgd_path(t_init, Xr, yr, l1, l2)
path_N = bgd_path(t_init, Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
plt.subplot(221 + i * 2)
plt.grid(True)
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.contourf(t1, t2, J, levels=levelsJ, alpha=0.9)
plt.contour(t1, t2, N, levels=levelsN)
plt.plot(path_J[:, 0], path_J[:, 1], "w-o")
plt.plot(path_N[:, 0], path_N[:, 1], "y-^")
plt.plot(t1_min, t2_min, "rs")
plt.title(r"$\ell_{}$ penalty".format(i + 1), fontsize=16)
plt.axis([t1a, t1b, t2a, t2b])
if i == 1:
plt.xlabel(r"$\theta_1$", fontsize=20)
plt.ylabel(r"$\theta_2$", fontsize=20, rotation=0)
plt.subplot(222 + i * 2)
plt.grid(True)
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
plt.plot(path_JR[:, 0], path_JR[:, 1], "w-o")
plt.plot(t1r_min, t2r_min, "rs")
plt.title(title, fontsize=16)
plt.axis([t1a, t1b, t2a, t2b])
if i == 1:
plt.xlabel(r"$\theta_1$", fontsize=20)
plt.show()
根据sklearn的Lasso实现的的小栗子:
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X,y)
lasso_reg.predict([[1.5]])

同样也可以使用SGDRegressor(penalty='l1')来实现它
弹性网络(Elastic Net)
弹性网络介于Ridge回归和Lasso回归之间,它的正则项是Ridge回归和Lasso回归正则项的简单混合,同时可以控制疼的混合率r,让r=0时,弹性网络就是Ridge回归,r=1时,就是Lasso回归,公式如下:
plot_model(ElasticNet,polynomial=True,alphas=(0,0.1,0.5),random_state=42)
效果展示:
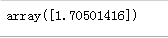
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1,l1_ratio=0.5,random_state=42)
elastic_net.fit(X,y)
elastic_net.predict([[1.5]])
那问题来了,如何选择呢?一般来说有一点正则项的表现更好,因此通常要避免使用简单的线性回归。岭回归是一个很好的首选项,但如果特征仅有少数是真正有用的,应该选择Lasso和弹性网络
早期停止法(Early stopping)
对于迭代学习算法,有一种非常特殊的正则化方法,就像梯度下降在验证错误达到最小值时立即停止训练那样,称为早期停止法。
使用批量梯度下降来训练一个复杂的模型(高阶多项式回归模型)
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m,1) -3
y = 2 + X + 0.5 * X**2 +np.random.randn(m,1)
X_train,X_val,y_train,y_val = train_test_split(X[:50],y[:50].ravel(),test_size=0.5,random_state=10)
poly_scaler = Pipeline([
('poly_features',PolynomialFeatures(degree=90,include_bias=False)),
('std_scaler',StandardScaler()),
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1,
tol=-np.infty,
penalty=None,
eta0=0.0005,
warm_start=True,
learning_rate='constant',
random_state=42)
n_epochs = 500
train_errors,val_errors=[],[]
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled,y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train,y_train_predict))
val_errors.append(mean_squared_error(y_val,y_val_predict))
best_epoch= np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
xy=(best_epoch,best_val_rmse),
xytext=(best_epoch,best_val_rmse+1),
ha='center',
arrowprops=dict(facecolor='black',shrink=0.05),
fontsize=16)
best_val_rmse -= 0.03
plt.plot([0, n_epochs],[best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors),'b-',linewidth=3,label='Valdation Set')
plt.plot(np.sqrt(train_errors),'r--',linewidth=3,label='Training Set')
plt.legend(loc='upper right',fontsize=14)
plt.xlabel('Epoch',fontsize=14)
plt.ylabel('RMSE',fontsize=14)
plt.show()
注意:当 warm_start=True 时,调用 fit() 方法后,训练会从停下来的地方继续,而不是从头重新开始
可视化展示:
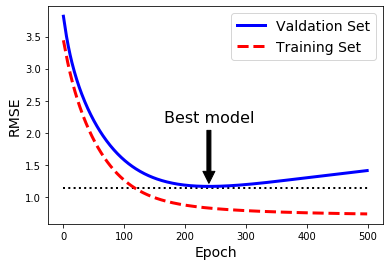
随着训练的进行,算法一直学习,它在训练集上的预测误差(RMSE)下降,但一段时间过后,验证误差停止下降,并开始上升。意味着模型在训练集上开始出现过拟合现象。一旦验证错误达到最小值,便提早停止训练。这种有效的正则化方法被Geoffrey Hinton称为“完美的免费午餐”
一个早期停止法的基础应用
from sklearn.base import clone
sgd_reg = SGDRegressor(max_iter=1,tol=-np.infty,warm_start=True,penalty=None,learning_rate='constant',eta0=0.0005,random_state=42)
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled,y_train)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val,y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
结果展示:




