观察学习曲线

• 交叉验证
  交叉验证可以用来估计一个模型的泛化能力，如果一个模型在训练集上表现良好，通过交叉验证指标却得出其泛化能力很差，那么模型就是过拟合了；如果这两个方面表现的都不好，那么它就是欠拟合了，这个方法可以告诉我们，模型是太复杂还是太简单了
• 观察学习曲线
  另一种方法就是观察学习曲线，画出模型在训练集上的表现，同时画出以训练集规模为自变量的训练集函数。为得到图像，需要在训练集的不同规模自己上进行多次训练。
  代码：

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curve(model,X,y):
    X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state = 10)
    train_errors,val_errors=[],[]
    for m in range(1,len(X_train)):
        model.fit(X_train[:m],y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_test)
        train_errors.append(mean_squared_error(y_train[:m],y_train_predict))
        val_errors.append(mean_squared_error(y_test,y_val_predict))
    plt.plot(np.sqrt(train_errors),'r-+',linewidth=2,label="train")
    plt.plot(np.sqrt(val_errors),'b-',linewidth=3,label='val')
    plt.legend(loc='upper left',fontsize=14)
    plt.xlabel('Traing set size',fontsize=14)
    plt.ylabel('RMSE',fontsize=14)

函数调用：

lin_reg = LinearRegression()
plot_learning_curve(lin_reg,X,y)
plt.axis([0,80,0,3])
plt.show()

效果展示：

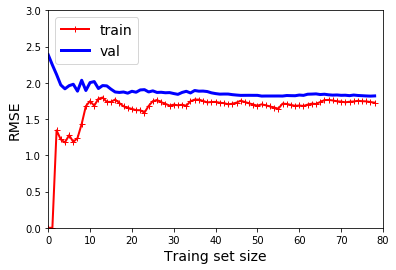
观察训练集的表现：当训练集只有一两个样本的时候，模型能够很好的拟合他们，这也是为什么曲线是从零开始的原因。但当加入了一些新的样本的时候，训练集上的拟合程度并不理想，原因有两个：1、数据中含有噪点；2、数据根本不是线性的。因此随着数据规模的增大，误差也会一直增大，直到达到了高原地带并趋于稳定，在在这之后，继续加入新的样本，模型的平均误差并不会变的更好或者更差。
验证集上的表现，当以非常少的样本去训练时，模型不能恰当的泛化，这也是为什么验证误差一开始非常大。当训练样本变多的时候，模型学习的东西变多，验证误差开始缓慢的下降。但是一条直线不可能很好的拟合这些数据，因此最后误差会达到一个高原地带并趋于稳定，最后和训练集的曲线非常接近。
上面的曲线表现的是典型的欠拟合模型，两条曲线都达到高原地带并趋于稳定，并且最后两条曲线非常接近，同时误差值非常大。
注意：
当模型在训练集上是欠拟合时，添加更多样本是没用的，需要做的是使用一个更加复杂的模型，或更好的特征。

现在我们来看下，在上面的数据集上使用10阶多项式模型拟合的效果

polynomial_regression = Pipeline([
    ('poly_features',PolynomialFeatures(degree=10,include_bias=False)),
    ('sgd_reg',LinearRegression())
])
plot_learning_curve(polynomial_regression,X,y)
plt.axis([0,80,0,3])
plt.show()

效果展示：

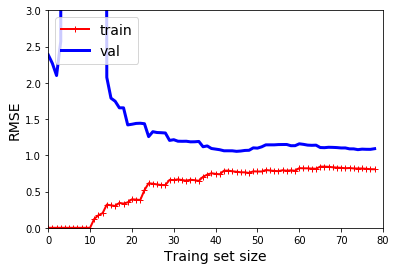
和上幅图像存在两个非常重要的不同点：

• 在训练集上，误差要比线性回归模型低的多
• 图中两条曲线之间有间隔，这意味着在训练集上的表现要比验证集上好的多，这也是模型过拟合的显著特征，当然，如果使用了更大的训练数据，这两条曲线最后非常接近。