线性回归的扩展---多项式回归

线性模型可以拟合线性问题，这是毋庸置疑的，但实际中处理的数据往往比直线更加复杂的非线性数据。这时，依然可以尝试使用线性模型来解决这个问题。

对每个特征进行加权后作为新的特征，然后在这个扩展的数据集上训练线性模型
啥意思呢，举个例子：
假设函数为：

\[h_\theta(x)=\theta_0+\theta_1(x)+\theta_2(x)^2 \]

转换函数：

\[x_1 = (x) \]

\[x_2 = (x)^2 \]

这样便得到了：

\[h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2 \]

这样便愉快实现了将非线性数据转换成了线性数据，困难是永远难不倒优秀的劳苦大众的
接下来，咱们又可以愉快的玩耍了
造数据(构造一个二次函数并加入噪点作为数据)

np.random.seed(42)
m = 100
X = 6* np.random.rand(m,1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m,1)

可视化显示：

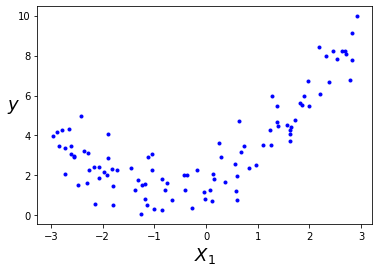
数据转换：
这里我们使用Sklearn中的PolynomialFeatures类将训练数据集进行转换，让训练集中每个特征的平方作为新特征

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2,include_bias=False)
X_poly = poly_features.fit_transform(X)
print(X[0])
print(X_poly[0])

结果展示：

这是可以发现，X_poly包含了原始特征X和这个特征的平方\(X^2\)。
扩展数据集有了，现在可以使用LinearRegression模型进行拟合

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)

查看截距和系数

lin_reg.intercept_,lin_reg.coef_

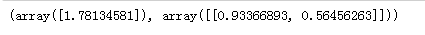
结果可视化显示

关于高阶的多项式回归
当存在多个特征时，多项式回归能够找出特征之间的关系（这是普通线性回归模型无法做到的），这是因为LinearRegression会自动添加当前阶数下特征的所有组合。例如：如果有两个特征a,b,使用3阶（degree=3）的LinearRegression时，不仅有\(a^2,a^3,b^2以及b^3\),同时也会有他们的其他组合项\(ab,a^2b,ab^2\)
注意：
PolynomialFeatures(degree=d)把一个包含n个特征的数组转换为一个包含\(\frac{(n+d)!}{d!n!}\)特征的数组，\(n!表示n的阶乘，等于1*2*....*n\),小心大量特征的组合爆炸
当使用一个高阶的多项式回归，还会存在一个问题，那就是过拟合
例如：同样是上面的数据，这次我们采用300阶的进行拟合，并同简单线性回归、2阶多项式回归做对比

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
for style,width,degree in (('g-',1,300),('b--',2,2),('r-+',2,1)):
    poly_big_features = PolynomialFeatures(degree= degree,include_bias=False)
    std_scaler = StandardScaler()
    lin_reg = LinearRegression()
    polynomial_regressor = Pipeline([('poly features',poly_big_features),
             ('std_scaler',std_scaler),
             ('linear reg',lin_reg)])
    polynomial_regressor.fit(X,y)
    y_newbig = polynomial_regressor.predict(X_new)
    plt.plot(X_new,y_newbig,style,label=str(degree),linewidth=width)

plt.plot(X,y,'b.',linewidth=3)
plt.axis([-3,3,0,10])
plt.xlabel('$X$',fontsize=18)
plt.ylabel("$y$",rotation=0,fontsize=18)
plt.legend(loc = "upper left")
plt.show()

可视化展示：

根据上面的对比，我们发现在这个训练集上，二次模型有着较好的泛化能力。那是因为在生成数据时使用的数据生成函数是二次函数，而通常我们是不知道这个数据生成函数是什么，那我们该如何决定我们模型的复杂度？模型是过拟合还是欠拟合呢？
一种是交叉验证
一种是观察学习曲线