论文学习：AGCRN

Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting
用于交通预测的自适应图卷积循环网络
会议：NIPS2020
作者：Lei Bai, Lina Yao, Can Li, Xianzhi Wang, Can Wang
论文地址：https://dl.acm.org/doi/10.5555/3495724.3497218
代码地址：https://github.com/LeiBAI/AGCRN

复现

GPU: A100

数据集	节点数量	MAE	MAPE	RMSE	epoch	时间消耗(h,min)
PEMS03	358	15.89	14.89	27.98	100	0h50
PEMS04	307	19.54	12.93	31.87	100	0h40
PEMS07	883	21.09	8.97	34.92	100	1h45
PEMS08	170	16.50	10.64	26.52	100	0h25

模型

节点自适应参数学习 NAPL-GCN

原本的GCN为：

\[Z=(I_N+D^{-\frac12}AD^{-\frac12})X\Theta+b \]

作者认为，不同节点模式不同，这种贡献参数\(\Theta\)的方式，只能捕获所有节点共有的信息，忽略了节点自己的信息
因此改为：

\[Z=(I_N+D^{-\frac12}AD^{-\frac12}) XE_{\mathcal{G}} W_{\mathcal{G}} + E_{\mathcal{G}} b_\mathcal G \]

按道理来说，是不能写成矩阵乘法的形式的，因为维数对不上，看看代码咋写的：
暂且不考虑代码中的batch数B和切比雪夫阶数K这两个维度，那么\((I_N+D^{-\frac12}AD^{-\frac12})\in R^{N\times N}\)，\(X\in R^{N\times C}\)，\(E_\mathcal G\in R^{N\times d}\)，\(W_\mathcal G\in R^{d\times C\times F}\)。先进行的是前两个\((N\times N)(N\times C)=(N\times C)\)和后两个\((N\times d)(d\times C\times F)=(N\times C\times F)\)，然后这两个相乘\((N\times C)(N\times C\times F)=(N\times F)\)。这里最后一个乘法不是常规的矩阵乘法，代码中使用einsum实现。

einsum：如矩阵乘法，可以写成np.einsum('ij,jk->ik', A, B)，其中：

• 在输入数组的标记之间，重复字母表示沿这些轴的值将相乘，这些乘积构成输出数组的值。
• 从输出标记中省略的字母表示沿该轴的值将被求和。

在上面(NxC)(NxCxF)->(NxF)的实例中，沿C轴的数字对应相乘，并求和。

数据自适应图生成 DAGG

作者认为预定义的图结构与预测任务没有直接关系，会导致很大偏差，因此完全使用自适应的图。直接训练出拉普拉斯矩阵：

\[D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=softmax(ReLU(\boldsymbol{E_A}\cdot\boldsymbol{E_A^T})) \]

其中\(E_A\in \mathbb R^{N\times d_e}\)表示节点嵌入，因此GCN表示成：

\[\boldsymbol{Z}=(\boldsymbol{I_N}+softmax(ReLU(\boldsymbol{E_A}\cdot\boldsymbol{E_A^T})))\boldsymbol{X\Theta} \]

图划分和子图训练的方法很好地解决自适应图生成的训练问题^[1]

图划分和子图训练这是什么？ 也没在代码上看到相应的部分，感觉像是加速计算的东西，再问问吧~ #不解

自适应图卷积循环网络 AGCRN

集成NAPL-GCN、DAGG和循环门控单元GRU：

\[\begin{aligned} &\tilde{\boldsymbol{A}}=softmax(ReLU(\boldsymbol{EE}^{\boldsymbol{T}})) \\ &z_{\boldsymbol{t}}=\sigma(\widetilde{A}[\boldsymbol{X}_{:,\boldsymbol{t}},\boldsymbol{h}_{\boldsymbol{t}-1}]\boldsymbol{E}\boldsymbol{W}_{\boldsymbol{z}}+\boldsymbol{E}\boldsymbol{b}_{\boldsymbol{z}} \\ &r_{t}=\sigma(\widetilde{A}[\boldsymbol{X}_{:,\boldsymbol{t}},\boldsymbol{h}_{\boldsymbol{t}-1}]\boldsymbol{E}\boldsymbol{W}_{r}+\boldsymbol{E}\boldsymbol{b}_{\boldsymbol{r}} \\ &\hat{\boldsymbol{h}}_{\boldsymbol{t}}=tanh(\widetilde{\boldsymbol{A}}[\boldsymbol{X}_{:,\boldsymbol{t}},\boldsymbol{r}\odot\boldsymbol{h}_{\boldsymbol{t}-1}]\boldsymbol{E}\boldsymbol{W}_{\boldsymbol{\hat{h}}}+\boldsymbol{E}\boldsymbol{b}_{\boldsymbol{\hat{h}}} \\ &h_{t}=z\odot h_{t-1}+(1-\boldsymbol{z})\odot\boldsymbol{\hat{h_{t}}} \end{aligned} \]

实验

对比试验结果：

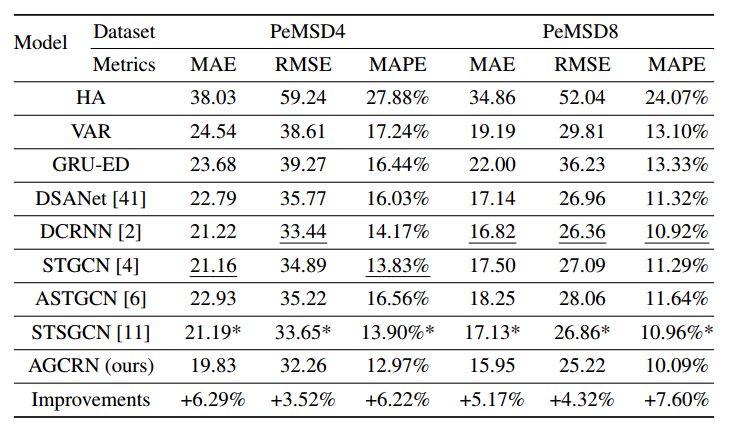AGCRN实验结果

作者还用实验寻找最合适的嵌入维数，实验证明是10最好。
作者还对DAGG进行了一些修改，然后比较结果。如去掉GCN公式中的单位矩阵，使用二阶切比雪夫多项式等。

总结

• 为每个节点单独设置参数的想法很好

---

1. section3.3 "Graph partition and sub-graph training methods" ↩︎