学习笔记：Graph WaveNet

Graph WaveNet for Deep Spatial-Temporal Graph Modeling
用于深度时空图模型的Graph WaveNet
期刊：IJCAI2019
作者：Zonghan Wu, Shirui Pan, Guodong Long, Jing Jiang, Chengqi Zhang
论文地址：https://www.ijcai.org/Proceedings/2019/0264
代码地址：https://github.com/nnzhan/Graph-WaveNet

这是一篇很经典的老论文，学这篇打好基础吧。

复现结果

GPU: A100（由于内存需求太大，部分数据集TITAN V无法运行）
下面的是保持模型原本的损失计算方法不变，只更改数据集的结果

数据集	节点数量	MAE	MAPE	RMSE	epoch	时间消耗(h,min)
PEMS03	358	15.04	14.49	25.36	100	0h45
PEMS04	307	19.89	14.52	31.27	100	0h25
PEMS07	883	21.27	9.71	34.09	100	2h10
PEMS08	170	15.44	10.00	24.30	100	0h20

模型

GraphWaveNet框架图

空间卷积结构

GCN通过聚合和转化邻域信息来平滑节点信号^[1]。
令\(\tilde A\in\mathbb R^{N\times N}\)为加了自环的归一化邻接矩阵

\(\tilde A\)构造方法：\(A\)归一化后，加上单位矩阵
( -(A/A.std).square ).exp + I
没有连边的位置为0

对于无向图，\(P=A/rowsum(A)\)，然后：

\[\mathbf{Z}=\sum_{k=0}^K\mathbf{P}^k\mathbf{X}\mathbf{W}_\mathbf{k} \]

对于有向图，正向转移为\(\mathbf{P}_f=\mathbf{A}/rowsum(\mathbf{A})\)，反向转移为\(\mathbf{P}_b=\mathbf{A}^\mathbf{T}/rowsum(\mathbf{A}^\mathbf{T})\)，然后：

\[\mathbf{Z}=\sum_{k=0}^K\mathbf{P}_f^k\mathbf{X}\mathbf{W}_{k1}+\mathbf{P}_b^k\mathbf{X}\mathbf{W}_{k2} \]

自适应邻接矩阵
随机生成节点嵌入\(\mathbf E_1, \mathbf E_2\in\mathbb R^{N\times c}\)（看起来就是在模型的开始随机生成的），自适应邻接矩阵为：

\[\mathbf{\tilde{A}}_{adp}=SoftMax(ReLU(\mathbf{E}_1\mathbf{E}_2^T)) \]

此时，自适应图卷积表示为：

\[\mathbf{Z}=\sum_{k=0}^K\mathbf{\tilde{A}}_{apt}^k\mathbf{X}\mathbf{W}_k \]

整个图卷积公式表示为邻接矩阵和自适应图两个卷积的和。

时间卷积结构

使用扩展因果卷积（dilated causal convolution）作为时间卷积层（TCN）

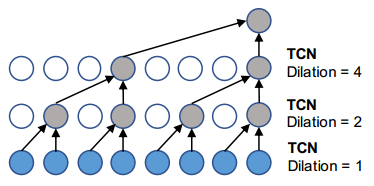GraphWaveNet TCN

与rnn方法相比，扩展因果卷积能够并行处理序列，有利于并行计算^[2]

在数学上，给定一个一维序列\(x\in\mathbb R^T\)和过滤器\(f\in\mathbb R^K\)，卷积操作表示为：

\[\mathbf{x}\star\mathbf{f}(t)=\sum_{s=0}^{K-1}\mathbf{f}(s)\mathbf{x}(t-d\times s) \]

其中\(d\)是扩展因子（dilation factior），表示跳过的距离。

TCN的实现需要看一下，是不是通过多层隐藏层实现的：
是这样的，有多个block，每个block有多个layer，其中每个block的第一层layer的d=1，然后依次d*=2

门控机制在控制时间卷积网络层间的信息流方面也很强大^[3]

总结

• “邻接矩阵+自适应邻接矩阵”的方式很好
• 扩展因果卷积的想法不错

---

1. Page3, section3.2 ↩︎

2. Page 3 section3.3 ↩︎

3. GraphWaveNet Page4 formula(9) ↩︎