学习笔记：傅里叶变换
本文目的是方便地理解傅里叶变换，不一定要掌握原理和计算方法，只要会用即可。
一、傅里叶级数
任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示，称为它的傅里叶级数，即：
也有另外一种写法：
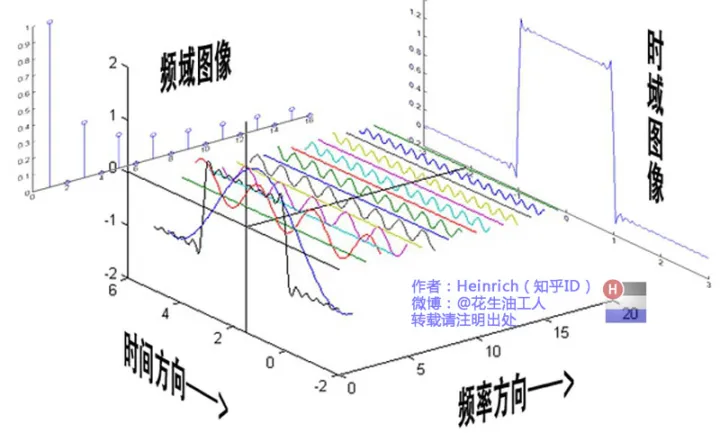
即分解为无数个余弦函数，带有各自的频率和相位。
 |
|---|
| 傅里叶级数 |
二、非周期函数的频率拆分
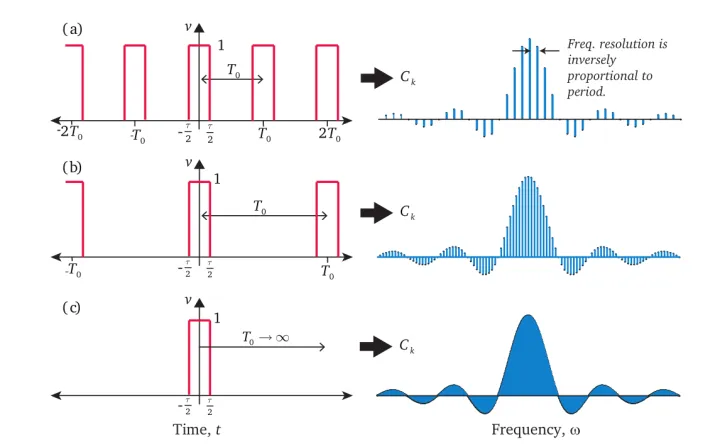
注意到傅里叶级数中的频率都是\(f(x)\)频率的倍数。随着\(f(x)\)的周期变大，其频率变小，那么傅里叶级数中的频率间隔变小。当T接近无限大，即\(f(x)\)没有周期时，傅里叶级数的频率会变得连续。也就是：
周期函数的频率组成是离散的；
非周期函数的频率组成是连续的。
 |
|---|
| 周期函数与非周期函数的频率图 |
三、傅里叶级数的求法
其基础是三角函数的正交性：频率不同的三角函数（\(\sin(nx)\)或\(\cos(mx)\)）相乘在一个周期内(x从-π到π)的积分必定为0
傅里叶级数表达式为：
\[f\left(t\right)=c_{0}+\sum_{n=1}^{\infty}c_{n}\cos\left(n\omega t+\varphi\right) \]
令\(a_n=c_n\cos\varphi,\ b_n=-c_n\sin\varphi\)，可以变换成：
\[f\left(t\right)=c_{0}+\sum_{n=1}^{\infty}\left[a_{n}\cos(\text{n}\omega\text{t})+b_{n}\sin(\text{n}\omega\text{t})\right] \]
对上式两边同时乘上\(\sin(k\omega t)\)并在一个周期上积分，得到：
根据三角函数的正交性，左边\(\int_0^Tf\left(t\right)\sin(k\omega t)dt\)只剩k频率\(b_k\int_0^T\sin(k\omega t)^2dt\)等于\(b_k\frac{T}{2}\)；右边\(\int_0^Tc_0\sin(k\omega t)\mathrm{d}t=0\)，也就得到了：
\[b_{n}=\frac{2}{T}\int_{0}^{T}f\left(t\right)\sin(n\omega t)\mathrm{d}t \]
同理，
\[a_n=\frac{2}{T}\int_0^Tf(t)\cos(n\omega t)\text{d}t \]
变换回去，也就是：
\[\begin{aligned}c_n&=\sqrt{{a_n}^2+{{b_n}^2}}\\\\\varphi&=\arctan\left(-\frac{b_n}{a_n}\right)\end{aligned} \]
四、傅里叶级数的复数表示
根据欧拉公式，\(e^{i\theta}=\cos\theta+i\sin\theta\)
利用\(\cos\theta\)是偶函数，\(\sin\theta\)是奇函数的性质，可以得到：
带入傅里叶级数中，并化简，得到：
由于：
\(\begin{aligned}a_{-n}&=\frac{2}{T}\int_0^Tf\left(t\right)\cos(-n\omega t)\text{dt}=a_n\\\\b_{-n}&=\frac{2}{T}\int_0^Tf\left(t\right)\sin(-n\omega t)dt=-b_n\end{aligned}\)
令\(A_{n}={\frac{(a_{n}-jb_{n})}{2}}\)，可将上式化简为：
\[f\left(t\right)=\sum_{n=-\infty}^{\infty}A_{n}e^{jn\omega t} \]
再次利用三角函数的正交性，向两边同时乘一个\(e^{-jk\omega t}\)，再在一个周期内积分，得到：
左边\(\int_0^Tf(t)e^{-jk\omega t}dt=\int_0^T A_ne^{jk\omega t} e^{-jk\omega t}dt=A_kT\)
也就是：
\[A_n=\frac{1}{T} \int_0^Tf(t)e^{-jn\omega t}dt \]
五、将\(T\)推向\(\infty\)
\(\omega=\frac{2\pi}{T}\to 0\)。\(A_n\)不再是离散的，写成\(F(\omega)\)。变为
\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \]\[F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \]
（对其中怎么推的还不清楚）
六、用质心的思想理解傅里叶变换
将\(e^{-i\omega t}\)看作是一个不停旋转的方向，其中\(w\)是超参数，\(t\)是自变量。那么\(f(t)e^{-i\omega t}\)就是向这个方向伸长了多少。随着自变量\(t\)的变化，\(f(t)\)将螺旋状地产生轨迹，那么上面的\(F(\omega)\)就是在\(\omega\)的转速下，\(f(t)\)形成的轨迹的质心。
 |
|---|
| 傅里叶变换与质心 |
当原曲线和转速不匹配时，轨迹会相对均匀地分布，质心距离原点近；当原曲线和转速匹配时，轨迹就会偏向于某一边，质心距离原点远。
如果画出在不同转速下，质心与原点的距离，这样得到的曲线，就是它的频率的组成分析，也就是傅里叶变换（其实还是有点不一样的，因为得到的只是一个复数）。
七、图像的傅里叶变换
将离散的复数形式的傅里叶变换，进行相应改写：
（为什么e的幂直接是两个相加呢）
（如果我没有理解错的话，\(u\in[0,2M],v\in[0,2N]\)）
这样，\(f(u,v)\)表示方向为从中心到(u,v)，频率为(u,v)到中心的距离（具体是什么距离，我不清楚）的三角函数。是一个复数，包含了振幅和相位信息。（所以具有中心对称性是吧）
 |
|---|
| 图片傅里叶变换-未中心化 |
 |
|---|
| 图片傅里叶变换-未中心化-物理含义 |
 |
|---|
| 图片傅里叶变换-中心化 |
实际上，应该分别画出实部和虚部才完整：
 |
|---|
| 图像傅里叶变化及旋转 |
中心点是全图灰度的均值（其它位置我暂时还无法理解）
摘抄自：
- b站：【官方双语】形象展示傅里叶变换
- 知乎：傅里叶变换推导详解
- 知乎：通俗讲解：图像傅里叶变换
可供参考的：
